Wavelet

Wavelet o ondicelle, analisi wavelet, e trasformata wavelet si riferiscono alla rappresentazione di un segnale mediante l'uso di una forma d'onda oscillante di lunghezza finita o a decadimento rapido (nota come wavelet madre). Questa forma d'onda è scalata e traslata per adattarsi al segnale in ingresso.

Storia

Lo sviluppo delle wavelet può essere collegato a diverse correnti di pensiero separate che hanno origine dal lavoro di Haar all'inizio del XX secolo. Contributi importanti alla teoria delle wavelet possono essere attribuiti alla formulazione, da parte di Goupillaud, Grossmann e Morlet, di quella che ora è nota come CWT (1982), ai lavori preliminari di Strömberg sulle wavelet discrete (1983), alle wavelet ortogonali a supporto compatto di Daubechies (1988), alla struttura a multirisoluzione di Mallat (1989), all'interpretazione in tempo-frequenza della CWT da parte di Delprat (1991), alla trasformata wavelet armonica di Newland e molti altri ancora.

Cronologia

• Prima wavelet (wavelet Haar) di Alfréd Haar (1909)
• Dagli anni '50: Jean Morlet e Alex Grossmann
• Dagli anni '80: Yves Meyer, Stéphane Mallat, Ingrid Daubechies, Ronald Coifman, Victor Wickerhauser

Descrizione

Introduzione

La parola wavelet, ondina, ha origine nei primi anni ottanta ed è dovuta a Morlet e Grossman che infatti usavano la parola francese ondelette (piccola onda). Poco più tardi la parola venne convertita in inglese traducendo "onde" ("onda" in francese) in "wave", ottenendo wavelet. Le trasformate wavelet sono classificate a livello generale nella trasformata wavelet discreta (Discrete Wavelet Transform, DWT) e nella trasformata wavelet continua (Continuous Wavelet Transform, CWT). La differenza di principio fra le due è il fatto che la trasformata continua opera su tutte le possibili scale e traslazioni, mentre la trasformata discreta usa un sottoinsieme discreto di tutti i valori possibili.

Utilità delle wavelet

La teoria delle wavelet è applicabile a molti campi. Tutte le trasformate wavelet possono essere considerate come forme di rappresentazioni in tempo-frequenza e sono quindi in relazione con l'analisi armonica. Quasi tutte le trasformate wavelet discrete utili in pratica usano dei banchi di filtri a risposta impulsiva finita. Le wavelet che costituiscono una CWT sono soggette al principio di indeterminazione di Heisenberg e allo stesso modo le basi delle trasformate wavelet discrete si possono considerare soggette ad altre forme di principio di indeterminazione.

Wavelet madre

In termini semplici, ma tecnicamente non corretti, la wavelet madre $\psi \ (t)$ deve soddisfare:

$\int _{-\infty }^{+\infty }|\psi (t)|\ ^{2}\,dt=1$, cioè $\psi \in L^{2}(\mathbb {R} )$ è normalizzata

$\int _{-\infty }^{+\infty }|\psi \ (t)|\,dt<+\infty$, cioè $\psi \in L^{1}(\mathbb {R} )$ è finita

$\int _{-\infty }^{+\infty }\psi \ (t)\,dt=0$, cioè a media nulla

Nella maggior parte delle situazioni è utile richiedere che $\psi$ sia continua e che abbia un numero alto M di momenti nulli, cioè per ogni intero m<M

$\int _{-\infty }^{+\infty }t^{m}\,\psi \ (t)\,dt=0$

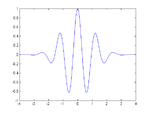
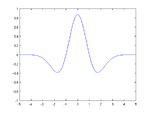
Questo significa che la wavelet madre deve essere non nulla e avere una media nulla. Tecnicamente la wavelet madre deve soddisfare un criterio di ammissibilità. Alcuni esempi di wavelet madre sono:

Meyer

Morlet

Mexican hat

La wavelet madre è scalata (o dilatata) di un fattore $a$ e traslata (o mossa) di un fattore $b$ per dare, nella formulazione originaria di Morlet:

$\psi _{a,b}(t)={1 \over {\sqrt {a}}}\psi \left({{t-b} \over a}\right)$

Queste funzioni sono spesso indicate erroneamente come le funzioni base della trasformata. Di fatto, non esiste una base. L'interpretazione in tempo-frequenza infatti richiede una formulazione leggermente diversa.

Confronto con Fourier

La trasformata wavelet è spesso paragonata alla trasformata di Fourier, dove i segnali sono rappresentati come somma di armoniche. La differenza principale è che le wavelet sono localizzate sia nel tempo sia nella frequenza mentre la trasformata di Fourier standard è localizzata solo in frequenza. La trasformata di Fourier a tempo breve (STFT) è localizzata in tempo e in frequenza, ma ci sono dei problemi di risoluzione e le wavelet spesso offrono una migliore rappresentazione del segnale grazie all'uso dell'analisi multirisoluzione.

La trasformata wavelet inoltre è anche meno complessa computazionalmente, richiedendo un tempo O(N) al contrario del tempo O(N log N) richiesto dalla trasformata di Fourier veloce (N indica la dimensione dei dati).

Definizione di wavelet

Esistono vari modi per definire una wavelet o una famiglia di wavelet.

Filtro di scalamento

La wavelet è completamente definita dal filtro di scalamento g, un filtro FIR (Finite Impulse Response) passa-basso di lunghezza 2N e somma 1. Nelle wavelet biortogonali sono definiti filtri distinti per la decomposizione e per la ricostruzione.

Il filtro passa-alto è definito come il filtro QMF (Quadrature Mirror Filter) del filtro passa-basso e il filtro di ricostruzione come il filtro a tempo invertito di quello di decomposizione.

Esempio: wavelet Daubechies e Symlet.

Funzione di scalamento

Le wavelet sono definite dalla funzione wavelet $\psi (t)$, cioè la wavelet madre, e dalla funzione di scalamento $\phi (t)$, detta anche wavelet padre, nel dominio del tempo.

La funzione wavelet è in effetti un filtro passa-banda e il suo scalamento ad ogni livello dimezza la sua banda. Questo crea il problema che, per coprire tutto lo spettro, sono richiesti un numero infinito di livelli. La funzione di scalamento filtra il livello più basso della trasformata e assicura che tutto lo spettro sia coperto. Vedi [1] per una spiegazione dettagliata.

Per una wavelet a supporto compatto, $\phi (t)$ può essere considerata di lunghezza finita ed è equivalente al filtro di scalamento g.

Esempio: wavelet Meyer.

Funzione wavelet

La wavelet ha solo una rappresentazione nel dominio del tempo come funzione wavelet $\psi (t)$.

e.g. wavelet "cappello messicano".

Applicazioni

Generalmente la DWT è usata nella codifica dei segnali mentre la CWT è usata nell'analisi dei segnali. Di conseguenza la DWT è usata comunemente in ingegneria e informatica e la CWT è usata più spesso nella ricerca scientifica. Le trasformate wavelet sono ora adottate in un gran numero di applicazioni, spesso sostituendo la trasformata di Fourier convenzionale. Molte aree della fisica hanno visto questo cambiamento di paradigma, inclusi la dinamica molecolare, il calcolo ab initio, l'astrofisica, la geofisica sismica, l'ottica, la turbolenza e la meccanica quantistica. Altre aree che stanno vedendo questo cambiamento sono l'elaborazione delle immagini, la misura della pressione del sangue, lo studio del battito del cuore e l'analisi dell'ECG, ;'analisi del DNA, l'analisi delle proteine, la climatologia, l'elaborazione dei segnali in generale, il riconoscimento vocale, la grafica computerizzata e l'analisi multifrattale.

Una delle applicazioni delle wavelet è la compressione di dati. Come molte altre trasformate, la trasformata wavelet può essere usata per trasformare dati grezzi. come le immagini per poi codificare i dati trasformati e ottenere un'effettiva compressione. Il formato JPEG 2000 è uno standard di immagini che usa le wavelet.

Trasformate wavelet

Esistono un gran numero di trasformate wavelet, ognuna adatta a una differente applicazione. Per una lista completa vedi elenco di trasformate wavelet, ma le più comuni sono qui elencate:

• Trasformata wavelet continua (CWT)
• Trasformata wavelet discreta (DWT)
• Trasformata wavelet veloce (FWT)
• Decomposizione in pacchetti wavelet (WPD)

Elenco di wavelet

Wavelet discrete

• Beylkin (18)
• Coiflet (6, 12, 18, 24, 30)
• Wavelet di Daubechies (2, 4, 6, 8, 10, 12, 14, 16, 18, 20)
• Wavelet di Cohen-Daubechies-Feauveau (talvolta riportata come Daubechies biortogonale, bior44=CDF9/7)
• Wavelet di Haar
• Filtro di Vaidyanathan (24)
• Symmlet
• Trasformata wavelet complessa

Wavelet continue

• Wavelet cappello messicano
• Wavelet hermitiana
• Wavelet di Morlet
• Wavelet di Morlet modificata
• Wavelet di Addison
• Wavelet hilbertiana-hermitiana

Bibliografia

• (EN) Paul S. Addison, The Illustrated Wavelet Transform Handbook, Institute of Physics, 2002, ISBN 0750306920
• (EN) Ingrid Daubechies, Ten Lectures on Wavelets, Society for Industrial and Applied Mathematics, 1992, ISBN 0898712742
• (EN) Mladen Victor Wickerhauser, Adapted Wavelet Analysis From Theory to Software, A K Peters Ltd, 1994, ISBN 1568810415
• (EN) P. P. Viadyanathan, Multirate Systems and Filter Banks, Prentice Hall, 1993, ISBN 0136057187

Voci correlate

• Banco di filtri
• Banda ultralarga
• Trasformata di Fourier a breve termine

Altri progetti

Altri progetti

• Wikimedia Commons

• Wikimedia Commons contiene immagini o altri file su Wavelet

Collegamenti esterni

• (EN) Wavelet Digest, su wavelet.org. URL consultato il 30 settembre 2005 (archiviato dall'url originale il 29 settembre 2020).
• (EN) Amaras Wavelet Page, su amara.com. URL consultato il 30 settembre 2005 (archiviato dall'url originale il 30 giugno 2007).
• (EN) Wavelet Posting Board, su ondelette.com. URL consultato il 30 settembre 2005 (archiviato dall'url originale il 1º ottobre 2005).
• (EN) The Wavelet Tutorial by Polikar, su users.rowan.edu. URL consultato il 30 settembre 2005 (archiviato dall'url originale il 10 febbraio 2004).
• (EN) OpenSource Wavelet C Code, su herbert.the-little-red-haired-girl.org.
• (EN) Filter Coefficients of Popular Wavelets, su mathworks.com.
• (EN) Wavelets for Kids (PDF file) (introduttivo)
• (EN) Link collection about wavelets, su cosy.sbg.ac.at.
• (EN) List of Wavelet resources, libraries and source codes, su compression-links.info. URL consultato il 30 settembre 2005 (archiviato dall'url originale il 1º dicembre 2005).
• (EN) A really friendly guide to wavelets, su perso.wanadoo.fr.
• Note sulle ondicelle (PDF), su caressa.it.

Controllo di autorità	Thesaurus BNCF 5390 · GND (DE) 4215427-3