Fenomeno di Runge

La curva rossa è la funzione di Runge, la curva blu è un polinomio di quinto grado, e la curva verde è un polinomio di nono grado. L'approssimazione, in prossimità degli estremi dell'intervallo, peggiora all'aumentare del grado.

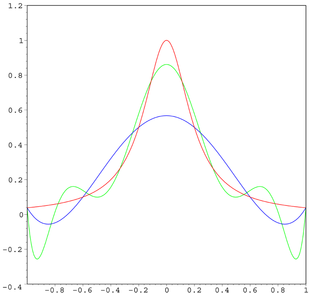
In analisi numerica il fenomeno di Runge è un problema relativo all'interpolazione polinomiale su nodi equispaziati con polinomi di grado elevato. Esso consiste nell'aumento di ampiezza dell'errore in prossimità degli estremi dell'intervallo.

È stato scoperto da Carl David Tolmé Runge mentre studiava il comportamento degli errori dell'interpolazione polinomiale per approssimare alcune funzioni.

Problema

Consideriamo la funzione:

$f(x)={\frac {1}{1+25x^{2}}}$

Runge trovò che interpolando questa funzione in un insieme di punti $x_{i}$ equidistanti nell'intervallo $\left[-1,1\right]$, con un polinomio $P_{n}(x)$ di grado $\leq n$, l'interpolazione risultante oscilla in ampiezza verso gli estremi dell'intervallo (in questo caso $-1$ e $+1$).

È inoltre possibile provare che tale errore tende all'infinito all'aumentare del grado del polinomio:

$\lim _{n\rightarrow +\infty }\left(\max _{x\in \left[-1,1\right]}\left|f(x)-P_{n}(x)\right|\right)=+\infty$

Soluzione

Il controesempio di Runge mostra che non è conveniente usare polinomi di grado elevato su nodi equispaziati per interpolare una funzione. Tuttavia è possibile ottenere uno schema di interpolazione il cui errore diminuisca all'aumentare del numero di nodi utilizzando i nodi di Čebyšëv in alternativa ai punti equidistanti. Altre alternative sono l'uso dell'interpolazione spline o l'uso dell'interpolazione composita, suddividendo l'intervallo di interpolazione in più parti e calcolando su ciascun sottointervallo un polinomio interpolante di grado non elevato (ad esempio grado 1 o 2).

Voci correlate

• Fenomeno di Gibbs per le funzioni sinusoidali
• Spline cubica di Hermite

Altri progetti

Altri progetti

• Wikimedia Commons

• Wikimedia Commons contiene immagini o altri file sul fenomeno di Runge