1 − 2 + 3 − 4 + · · ·

Rappresentazione su piano delle prime migliaia di termini del calcolo di 1 − 2 + 3 − 4 + ...

In matematica, 1 − 2 + 3 − 4 + ... è la serie infinita i cui termini sono la successione dei numeri interi a segno alternato. Usando la notazione di sommatoria, la somma dei primi $m$ termini della serie può essere espressa nel seguente modo:

$\sum _{n=0}^{m}n(-1)^{n+1}={\frac {1-{(2m+1)}{\cos({\pi }{m})}}{4}}.$

Le somme parziali di questa serie infinita (1, −1, 2, −2, ...), non tendono verso un limite, né finito, né infinito. In questo caso si può dire che 1 − 2 + 3 − 4 + ... è una serie indeterminata (o irregolare).

Nella metà del XVIII secolo, Leonhard Euler enunciò quella che lui definiva un'equazione paradossale:

$1-2+3-4+\cdots ={\frac {1}{4}}.$

Una corretta spiegazione di questa equazione arrivò solo molto più tardi. Nel 1890, Ernesto Cesaro, Émile Borel e altri matematici definirono i metodi per estendere il concetto di sommabilità secondo un punto di vista che rendeva possibile attribuire un limite anche a serie fino ad allora intrattabili. Questi nuovi metodi davano nuove interpretazioni all'equazione di Eulero. Molti di questi metodi sono riferiti alle somme parziali di 1 − 2 + 3 − 4 + ..., a cui assegnano il valore di ¹⁄₄. Nella somma di Cesaro, invece, i termini della successione non sono sommabili; questo è un esempio di successione per cui si rendono necessari metodi di sommabilità leggermente più forti, come ad esempio quelli della somma di Abel.

La serie 1 − 2 + 3 − 4 + … è strettamente legata alla serie 1 − 1 + 1 − 1 + …, nota più comunemente come serie di Grandi. Eulero considerò queste due successioni come casi particolari della serie 1ⁿ − 2ⁿ + 3ⁿ − 4ⁿ + …, per valori arbitrari di n. Queste idee estesero il suo studio del problema di Basilea indirizzarono la ricerca sulle equazioni funzionali delle funzioni che ora sono note come funzione eta di Dirichlet e funzione zeta di Riemann.

Divergenza

I termini della successione (1, −2, 3, −4, ...) non tendono a 0; quindi la non convergenza della relativa serie è una semplice conseguenza del più elementare dei criteri, quello che richiede quale condizione necessaria la convergenza a zero della successione.

È comunque utile, per il prosieguo, appurare il comportamento di questa serie analizzandola da un punto di vista più fondamentale. Per definizione, la convergenza o divergenza di una serie infinita è determinata dalla convergenza o divergenza della sua successione delle somme parziali; le somme parziali di 1 − 2 + 3 − 4 + ... sono:

• 1 = 1,
• 1 − 2 = −1,
• 1 − 2 + 3 = 2,
• 1 − 2 + 3 − 4 = −2,
• 1 − 2 + 3 − 4 + 5 = 3,
• 1 − 2 + 3 − 4 + 5 − 6 = −3, ...

In questa successione si nota che la serie assume tutti i valori interi diversi da zero (possiamo includere anche lo 0 se si considera la sommatoria vuota), fornendo peraltro una dimostrazione della numerabilità dell'insieme $\mathbb {Z}$ degli interi. Chiaramente, esso non si stabilizza su nessun numero particolare, e quindi 1 − 2 + 3 − 4 + ... è oscillante (mentre diverge in valore assoluto).

Metodi euristici per la sommabilità

Stabilità e linearità

Siccome i termini 1, −2, 3, −4, 5, −6, ... seguono uno schema semplice, la serie 1 − 2 + 3 − 4 + ... può essere manipolata con opportuni spostamenti dei termini della somma al fine di ottenere un valore finito. È possibile dare un senso a un'espressione come s = 1 − 2 + 3 − 4 + ... per qualche intero s: ad esempio, le seguenti manipolazioni, la rendono valida per s = ¹⁄₄:

${\begin{array}{rclllll}4s&=&&(1-2+3-4+\cdots )&+(1-2+3-4+\cdots )&+(1-2+3-4+\cdots )&+(1-2+3-4+\cdots )\\&=&&(1-2+3-4+\cdots )&+1+(-2+3-4+5+\cdots )&+1+(-2+3-4+5+\cdots )&-1+(3-4+5-6+\cdots )\\&=&1+[&(1-2-2+3)&+(-2+3+3-4)&+(3-4-4+5)&+(-4+5+5-6)+\cdots ]\\&=&1+[&0+0+0+0+\cdots ]\\4s&=&1\end{array}}$

Così $s={\frac {1}{4}}.$

Aggiungendo 4 copie di 1 − 2 + 3 − 4 + ... usando solo lo spostamento dei termini dell'addizione, il risultato è 1. È stato aggiunto il calcolo 1 − 1 + 1 − 1 + ..., la serie di Grandi.

In alternativa, si possono scrivere le seguenti 4 uguaglianze e sommare membro a membro:

${\begin{aligned}s=1-2+3-4+5-6+\cdots \\s=\ \ \ \ \ \ \ 1-2+3-4+5-\cdots \\s=\ \ \ \ \ \ \ 1-2+3-4+5-\cdots \\s=\ \ \ \ \ \ \ \ \ \ \ \ \ \ 1-2+3-4+\cdots \\{\text{------------------------------------------}}\\4s=1+0+0+0+0+0+\cdots \end{aligned}}$

ossia $4s=1,$ cioè $s={\frac {1}{4}}.$

Il risultato di questo calcolo viene rappresentato graficamente sulla destra.

Nonostante 1 − 2 + 3 − 4 + ... non abbia una somma intesa nel senso abituale, l'equazione s = 1 − 2 + 3 − 4 + ... = ¹⁄₄ può essere un esempio naturale per descrivere come un'estensione del concetto di somma possa essere definita. Una definizione generalizzata di somma per una serie che ordinariamente non è convergente, è chiamato un metodo di sommabilità, in cui la somma viene effettuata solo su alcuni sottoinsiemi dell'indice delle possibili serie.

Esistono metodi di questo tipo, e alcuni di questi sono indicati in seguito, ciascuno dei quali si caratterizza per le proprietà che condivide con il concetto ordinario di addizione.

Quello che la manipolazione sopra descritta sottende è che dato un metodo di sommabilità che sia lineare e stabile, che consenta la sommabilità della serie 1 − 2 + 3 − 4 + ..., allora il risultato della somma deve essere ¹⁄₄. Inoltre, siccome ${\begin{array}{rcllll}2s&=&&(1-2+3-4+\cdots )&+&(1-2+3-4+\cdots )\\&=&1+&(-2+3-4+\cdots )&+1-2&+(3-4+5\cdots )\\&=&0+&(-2+3)+(3-4)+(-4+5)+\cdots \\{\frac {1}{2}}&=&&1-1+1-1\cdots \\\end{array}}$

allora questo metodo di sommabilità deve rendere sommabile anche la serie di Grandi, dando come risultato s = 1 − 1 + 1 − 1 + ... = ¹⁄₂.

Un altro metodo, che sfrutta appunto il risultato della serie di Grandi è il seguente:

${\begin{array}{rclllll}s&=&(1-2)+3+(-4+5)-6+(7-8)+9\cdots \\&=&(-1+1-1+1\cdots )+(3-6+9-12+\cdots )\\[0.4em]&=&-{\frac {1}{2}}+3\cdot (1-2+3-4+\cdots )\\[0.4em]s&=&-{\frac {1}{2}}+3s\\[0.4em]s&=&{\frac {1}{4}}\\\end{array}}$

Successione di Cauchy

Una dimostrazione grafica del fatto che 1 − 2 + 3 − 4 + … equivale al prodotto di Cauchy tra 1 − 1 + 1 − 1 + … e 1 − 1 + 1 − 1 + …

Nel 1891, Ernesto Cesaro espresse la speranza che le serie divergenti avessero costituito importanti metodi nei calcoli matematici, puntando verso la teoria nella quale (1 − 1 + 1 − 1 + …) 2 = 1 − 2 + 3 − 4 + … equivale a ¹⁄₄. Per Cesaro questa equazione fu un'applicazione di un teorema che aveva pubblicato l'anno prima, il quale fu ritenuto il primo nella storia delle serie divergenti. I dettagli di questo metodo per la sommabilità sono nell'idea centrale la quale ritiene che 1 − 2 + 3 − 4 + … è il prodotto di Cauchy di 1 − 1 + 1 − 1 + … e 1 − 1 + 1 − 1 + ….

Il prodotto di Cauchy, scoperto dal matematico francese Augustin-Louis Cauchy, è costituito a partire da due serie infinite. Nel caso in cui Σa_n = Σb_n = Σ(−1)ⁿ, i termini della serie di Cauchy sono dati da una somma finita:

${\begin{array}{rcl}c_{n}&=&\displaystyle \sum _{k=0}^{n}a_{k}b_{n-k}=\sum _{k=0}^{n}(-1)^{k}(-1)^{n-k}\\[1em]&=&\displaystyle \sum _{k=0}^{n}(-1)^{n}=(-1)^{n}(n+1).\end{array}}$

Il prodotto della serie è quindi il seguente:

$\sum _{n=0}^{\infty }(-1)^{n}(n+1)=1-2+3-4+\cdots .$

Così una somma che rispetta la successione di Cauchy, ossia due serie finite combacianti con 1 − 1 + 1 − 1 + … = ¹⁄₂ e 1 − 2 + 3 − 4 + … = ¹⁄₄, si avranno come risultato ¹⁄₂ e ¹⁄₄. Con il risultato della prima serie, si ha un'equivalenza tra la somma di 1 − 1 + 1 − 1 + … e quella di 1 − 2 + 3 − 4 + …, perciò questo metodo è lineare, stabile e rispetta la successione di Cauchy.

La somma di Cesaro è un semplice esempio di serie divergente. La serie 1 − 1 + 1 − 1 + … è sommabile, secondo il teorema di Cesaro, in modo parziale; questo tipo di calcolo è chiamato $(C,1)$-sommabile. 1 − 2 + 3 − 4 + … invece non necessita di un supporto del teorema di Cesaro, per questo motivo è definita $(C,2)$-sommabile. Per essere utilizzato in una serie, la somma di Cesaro deve quindi incontrarne una lineare e stabile.

Metodi specifici

Cesaro e Hölder

Dati sulla somma (H, 2) di ¹⁄₄.

Per trovare in una somma di Cesaro la sommabilità $(C,1)$ di 1 − 2 + 3 − 4 + …, se essa esiste, bisogna applicare il concetto della media aritmetica alle somme parziali delle serie, le quali sono, in questa serie:

1, −1, 2, −2, 3, −3, …,

Le medie aritmetiche sono perciò le seguenti:

1, 0, ²⁄₃, 0, ³⁄₅, 0, ⁴⁄₇, ….

Questa successione non converge, in questo caso 1 − 2 + 3 − 4 + … non è sommabile con i criteri del teorema di Cesaro.

Ci sono due generalizzazioni molto conosciute della somma di Cesaro: il semplice concetto che ritiene che la somma $(H,n)$ opera sui numeri naturali $n.$ La $(H,1)$ somma di Cesaro, per essere applicata, necessita di una serie nella quale bisogna trovare molte medie matematiche. Così, la media regolare converge a ¹⁄₂, e le somme dispari sono uguali a 0. In questo caso la media della media converge a 0 e ¹⁄₂, cioè ¹⁄₄. Così, 1 − 2 + 3 − 4 + … è (H, 2) sommabile per ¹⁄₄.

La $H$ è la parte dell'equazione trovata da Otto Hölder, il quale dimostrò nel 1882 quello che oggi in matematica si intende per legame tra la somma di Abel e i metodi per la somma $(H,n)$ di 1 − 2 + 3 − 4 + …; questa successione fu la prima alla quale venne applicata questa regola. Il fatto che ¹⁄₄ sia la somma $(H,2)$ di 1 − 2 + 3 − 4 + … garantisce che si può applicare la somma di Abel a questa serie.

Un'altra generalizzazione della somma di Cesaro è la successione dei metodi $(C,n).$ Egli ha infatti dimostrato che la somma $(C,n)$ e la somma $(H,n)$ danno lo stesso risultato, nonostante il diverso contesto storico. Nel 1887, Cesaro cercò una definizione per la regola della somma $(C,n),$ ma riuscì a fornire solo pochi esempi. In particolare, ha sommato 1 − 2 + 3 − 4 + … con ¹⁄₄ con un metodo strettamente legato a $(C,n),$ ma non ha giustificato come lo ha fatto. Egli, nel 1890, definiva i metodi $(C,n)$ in stati ordinati del suo teorema con l'ausilio della successione di Cauchy grazie a una serie $(C,n)$-sommabile e a una serie $(C,m)$-sommabile, facendo risultare il tutto $(C,m+n+1)$-sommabile.

Somma di Abel

Somme parziali di 1−2x+3x²+…; 1/(1 + x)²; il risultato sarà sempre 1.

In un documento del 1749, Eulero ammette che una serie diverge ma non ha una somma precisa.

(EN)

«When it is said that the sum of this series 1 − 2 + 3 − 4 + 5 − 6 ... is ¹⁄₄, that must appear paradoxical. For by adding 100 terms of this series, we get –50, however, the sum of 101 terms gives +51, which is quite different from ¹⁄₄ and becomes still greater when one increases the number of terms. But I have already noticed at a previous time, that it is necessary to give to the word sum a more extended meaning.»

(IT)

«Quando si dice che il risultato tra le somme della serie 1 − 2 + 3 − 4 + 5 − 6 ... è ¹⁄₄, questo fatto deve apparire paradossale. Addizionando 100 termini di questa serie, si avrà un risultato di –50, comunque, sommando il risultato con 101 si ha +51; perciò il risultato totale non dovrebbe essere ¹⁄₄. Ma io avevo già annunciato in precedenza, che è necessario dare alla parola « somma » una definizione più approfondita.»

(Eulero, 1749.)

Eulero ha proposto nuove definizioni della parola somma varie volte, pubblicando il libro Euler on infinite series (letteralmente Eulero sulle serie infinite). Nel caso della serie 1 − 2 + 3 − 4 + …, le sue idee sulla somma sono simili a quelle utilizzate per la somma di Abel.

(EN)

«It is no more doubtful that the sum of this series 1 − 2 + 3 − 4 + 5 + ... is ¹⁄₄; since it arises from the expansion of the formula ¹⁄_(1+1)², whose value is incontestably ¹⁄₄. The idea becomes clearer by considering the general series 1-2x + 3x² - 4x³ + 5x⁴ - 6x⁵ ... that arises while expanding the expression ¹⁄_(1+x)², which this series is indeed equal to after we set $x=1$.»

(IT)

«Non c'è dubbio che il risultato della somma di 1 − 2 + 3 − 4 + 5 + ... sia ¹⁄₄; poiché proviene dall'espansione della formula ¹⁄_(1+1)², il quale valore è di ¹⁄₄. L'idea risulta più chiara dalla considerazione della serie generale 1-2x + 3x² - 4x³ + 5x⁴ - 6x⁵ ... che si genera espandendo l'espressione ¹⁄_(1+x)², alla quale la serie è evidentemente uguale ponendo $x=1$.»

(Eulero, 1749.)

Ci sono molti modi per vedere che, almeno per i valori $|x|<1,$ Eulero ha ragione nel porre

$1-2x+3x^{2}-4x^{3}+\cdots ={\frac {1}{(1+x)^{2}}}.$

Uno modo è usare lo sviluppo di Taylor al secondo membro.

Da un punto di vista moderno, la serie 1 − 2x + 3x² − 4x³ + … non definisce una funzione per $x=1,$ quindi tale valore non può essere semplicemente sostituito nell'espressione. Poiché questa funzione è definita per $|x|<1,$ se ne può calcolare il limite per $x\to 1$ e questa è la definizione della somma di Abel:

$\lim _{x\rightarrow 1^{-}}\sum _{n=1}^{\infty }n(-x)^{n-1}=\lim _{x\rightarrow 1^{-}}{\frac {1}{(1+x)^{2}}}={\frac {1}{4}}.$

Eulero e Borel

La somma di Eulero di ¹⁄₂ − ¹⁄₄.

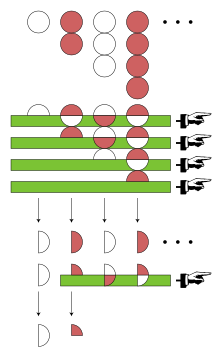
Eulero ha applicato un altro metodo per il calcolo nelle serie: una trasformazione binomiale di sua invenzione. Per calcolare la trasformazione binomiale di Eulero, si inizia con una successione di termini positivi, che poi formerà la serie alternata, in questo caso si ha 1, 2, 3, 4, …. Il primo elemento di questa successione è indicato con $a_{0}.$

Poi si devono calcolare le differenze in avanti tra 1, 2, 3, 4, …; che sono 1, 1, 1, 1, …. Il primo elemento in questa successione è indicato con $\Delta a_{0}.$ La numerazione binomiale dipende anche dalle differenze di differenze, ma tutte le differenze in avanti tra 1, 1, 1, 1, … sono 0. La trasformazione di Eulero di 1 − 2 + 3 − 4 + … è anche definibile come:

${\frac {1}{2}}a_{0}-{\frac {1}{4}}\Delta a_{0}+{\frac {1}{8}}\Delta ^{2}a_{0}-\cdots ={\frac {1}{2}}-{\frac {1}{4}}.$

Nella terminologia moderna si dice che la serie 1 − 2 + 3 − 4 + ... è sommabile mediante la somma di Eulero e vale ¹⁄₄. Secondo la somma di Eulero, in questa serie bisogna applicare un ulteriore tipo di criterio di sommabilità, rappresentando 1 − 2 + 3 − 4 + … come

$\sum _{k=0}^{\infty }a_{k}=\sum _{k=0}^{\infty }(-1)^{k}(k+1),$

si ha la serie convergente ovunque:

$a(x)=\sum _{k=0}^{\infty }{\frac {(-1)^{k}(k+1)x^{k}}{k!}}=e^{-x}(1-x).$

La somma di Borel applicata nella serie 1 − 2 + 3 − 4 + ... sarà quindi

$\int _{0}^{\infty }e^{-x}a(x)\,dx=\int _{0}^{\infty }e^{-2x}(1-x)\,dx={\frac {1}{2}}-{\frac {1}{4}}.$

Separazione delle misure

Aleksander Saičev e Wojbor Andrzej Woyczyński arrivarono a 1 − 2 + 3 − 4 + … = ¹⁄₄ applicando due principi fisici: la relazione infinitesima e la separazione delle misure. Per essere precisi, questi principi fanno parte di una lunga famiglia denominata metodi φ-sommabili, le cui somme, in questa serie, risultano ¹⁄₄: se $\varphi (x)$ è una funzione con derivata prima e seconda continue e integrabili in $(0,+\infty ),$ tali che $\varphi (0)=1$ e i limiti di $\varphi (x)$ e $x\varphi (x)$ a $+\infty$ siano 0.

$\lim _{\delta \to 0}\sum _{m=0}^{\infty }(-1)^{m}(m+1)\varphi (\delta m)={\frac {1}{4}}.$

Questo risultato generalizza la somma di Abel, la quale si ottiene applicando $\varphi (x)=e^{-x}.$ Il risultato generale può essere dimostrato accoppiando i termini della serie su $m$ e convertendo l'espressione in un integrale di Riemann. Per l'ultimo passaggio, nella dimostrazione corrispondente per 1 − 1 + 1 − 1 + … si applica il teorema del valor medio, ma serve una forma di Lagrange più forte del teorema di Taylor.

Generalizzazioni

Somme di Eulero nel suo libro del 1755 Istituzioni.

Il prodotto di Cauchy di 1 − 1 + 1 − 1 + … per sé stesso tre volte è 1 − 3 + 6 − 10 + …, ossia la serie alternata di un numero triangolare. Secondo la somma di Abel e la somma di Eulero il risultato è ¹⁄₈. Il prodotto di Cauchy di 1 − 1 + 1 − 1 + … per sé stesso quattro volte è 1 − 4 + 10 − 20 + …, ossia la serie alternata di un numero tetraedrico. Secondo la somma di Abel il risultato è ¹⁄₁₆.

Un'altra generalizzazione di 1 − 2 + 3 − 4 + … in una direzione leggermente diversa è la serie 1 − 2ⁿ + 3ⁿ − 4ⁿ + … per altri valori di $n.$ Per un numero intero positivo $n,$ queste serie operano con la somma di Abel nel seguente modo:

$1-2^{n}+3^{n}-\cdots ={\frac {2^{n+1}-1}{n+1}}B_{n+1}.$

Qui $B_{n}$ sono i numeri di Bernoulli. Per $n$ pari, la serie si riduce:

$1-2^{2k}+3^{2k}-\cdots =0.$

L'ultima somma diventa oggetto di derisione da parte Niels Henrik Abel nel 1826:

(EN)

«Divergent series are on the whole devil's work, and it is a shame that one dares to found any proof on them. One can get out of them what one wants if one uses them, and it is they which have made so much unhappiness and so many paradoxes. Can one think of anything more appalling than to say that $0=1-2^{n}+3^{n}-4^{n}+\ldots$ where n is a positive number. Here's something to laugh at, friends.»

(IT)

«Le serie divergenti sono tutte lavoro del diavolo, ed è una vergogna cercare ipotesi e teorie su di esse. Si può trarre qualcosa da esse se si vuole veramente usarle, e questo le rende così infelici e paradossali. Si possono pensare cose molto più scioccanti se però si dice che $0=1-2^{n}+3^{n}-4^{n}+\ldots$ dove n è un numero positivo. Qui c'è da ridere, amici.»

(Grattan-Giunness, p. 80.)

Anche l'insegnante di Cesaro, Eugène Charles Catalan, denigrava le serie divergenti. Sotto l'influenza di Catalan, inizialmente Cesaro fece riferimento a "formule convenzionali" come 1 − 2ⁿ + 3ⁿ − 4ⁿ + … e a "uguaglianze assurde", e nel 1883 espresse un tipico punto di vista di quel periodo sul fatto che le formule fossero false ma, in qualche modo, comunque utili. Per finire, nel suo libro Sur la multiplication des séries del 1890, Cesaro seguì un approccio moderno partendo dalle definizioni.

Le serie sono inoltre studiate per i valori non interi di n; questo ha consentito la scoperta della funzione eta di Dirichlet. Parte delle motivazioni degli studi di Eulero sulla serie 1 − 2 + 3 − 4 + … riguardano l'equazione funzionale della funzione eta, la quale porta direttamente all'equazione funzionale della funzione zeta di Riemann. Eulero è diventato famoso anche per aver trovato i valori di queste funzioni per numeri interi pari (includendo il problema di Basilea), e per aver tentato di trovare i loro valori con numeri interi dispari (includendo la costante di Apéry). La funzione eta, in particolare, è facile da studiare con i metodi di Eulero perché la sua serie di Dirichlet è sommabile ovunque utilizzando la somma di Abel. La funzione zeta della serie di Dirichlet è molto difficile da sommare dove essa diverge. Per esempio, la corrispondente di 1 − 2 + 3 − 4 + … nella funzione zeta è la serie non alternata 1 + 2 + 3 + 4 + …, alla quale sono stati applicati recentemente metodi fisici che necessitano però di metodi di somma più elaborati.

Bibliografia

• (EN) Richard Beals, Analysis: an introduction, Cambridge UP, 2004, ISBN 0-521-60047-2.
• (EN) Harry Davis, Fourier Series and Orthogonal Functions. Dover, 1989. ISBN 0-486-65973-9
• (FR) Leonhard Euler, Remarques sur un beau rapport entre les séries des puissances tant directes que réciproques, Memoires de Berlin, 1978..
• (EN) Giovanni Ferraro, The First Modern Definition of the Sum of a Divergent Series: An Aspect of the Rise of 20th Century Mathematics , in Archive for History of Exact Sciences, vol. 54, giugno 2019, pp. 101-135, DOI:10.1007/s004070050036.
• (EN) Ivor Grattan, The development of the foundations of mathematical analysis from Euler to Riemann. MIT Press, 1970. ISBN 0-262-07034-0
• (EN) Godfrey Harold Hardy, Divergent Series, Clarendon Press, 1949, LCCN 91075377.
• (EN) Morris Kline, Euler and Infinite Series, in Mathematics Magazine, n. 56, 1983.
• (EN) Shaughan Lavine, Understanding the Infinite. Harvard UP, 1994. ISBN 0-674-92096-1
• (RU) Aleksandr Markuševič, Series: fundamental concepts with historical exposition, Hindustan, 1961.
• (RU) Ivan Saičev, Distributions in the physical and engineering sciences, Volume 1. Birkhaüser, 1996. ISBN 0-8176-3924-1
• (EN) John Tucciarone, The development of the theory of summable divergent series from 1880 to 1925 , in Archive for History of Exact Sciences, vol. 10, gennaio 1973, DOI:10.1007/BF00343405.
• (EN) Anders Vretblad, Fourier Analysis and Its Applications. Springer, 2003. ISBN 0-387-00836-5
• (EN) John Weidlič, Summability methods for divergent series, Stanford, 1950, OCLC 38624384.

Voci correlate

• Serie di Grandi
• Serie sommativa unitaria
• 1 + 2 + 3 + 4 + · · ·
• 1 − 2 + 4 − 8 + · · ·
• 1 + 2 + 4 + 8 + · · ·
• 1 − 3 + 9 − 27 + · · ·
• 1 − 1 + 2 − 6 + 24 − 120 + ...
• Euristica

Collegamenti esterni

• (EN) Equazioni e formule per 1 − 2 + 3 − 4 + ..., su home.scarlet.be. URL consultato il 28 febbraio 2008 (archiviato dall'url originale il 26 dicembre 2012).