Topografia


La topografia (dal greco τοπογραϕία, comp. di τόπος topos, luogo e γραϕία grafia, scrittura) è la scienza che ha come scopo la determinazione e la rappresentazione metrica con il disegno in una mappa con segni convenzionali della superficie terrestre. Ha carattere applicativo e trae la sua base teorica dalle scienze pure: la matematica, la geometria e la fisica.
Storia della topografia[modifica | modifica wikitesto]
Le origini della topografia sono remote, ma si sa che il termine era già usato da Strabone. Nell'antico Egitto gli agrimensori riconfinavano i terreni inondati dalle piene del Nilo. I romani riferivano ciascun rilevamento a due assi perpendicolari, tracciati con la groma e misurati con pertiche: il decumano, con orientazione est-ovest, e il cardo, con orientazione nord-sud, ai quali riferivano un reticolato di 2400 piedi (700 m circa) di lato. Metodi simili furono usati fino alla fine del Medioevo.
Solo nel XVII secolo in Svezia, nei Paesi Bassi e in Francia, si cominciarono a eseguire lavori topografici di una certa importanza. La prima carta topografica di concezione moderna fu la carta di Francia alla scala 1:86.400 iniziata nel 1744 da César François Cassini di Thury-sous-Clermont. L'Italia annovera famosi topografi tra i quali possiamo citare Ignazio Porro, Giovanni Boaga e il generale Giuseppe Birardi per ciò che concerne la geodesia.
In particolare Ignazio Porro è riconosciuto essere il padre della celerimensura, ossia il metodo di triangolazione basato sulla determinazione, da una base di stazionamento, di tre valori fondamentali di un secondo punto del territorio: distanza in linea d'aria dalla stazione, angolo orizzontale, angolo zenitale, oltre alla determinazione dell'altezza strumentale e l'altezza del prisma di collimazione (o della stadia). La celerimensura, introdotta nel 1822 proprio dal brillante ingegnere italiano, è ancora oggi la tecnica principale di rilevazione topografica diretta alla media distanza nel mondo. L'ingegnere italiano utilizzava per tale tecnica il celerimetro, una versione estremamente semplificata degli attuali teodolite e stazione totale.
Descrizione[modifica | modifica wikitesto]
Geodesia e topografia teoretica[modifica | modifica wikitesto]
L'intento della geodesia è quello di approssimare la superficie effettiva della Terra, e ciò avviene tramite diverse superfici di riferimento:
- superficie dinamica teorica: è una particolare superficie del campo teorico della gravità terrestre. Ipotizzando che la Terra sia un corpo continuo di densità uniforme, con moto costante attorno al suo asse di rotazione. Questa superficie è sempre di natura teorica ma già legata a un'entità fisica reale, il campo gravitazionale.
- superficie dinamica reale: è una particolare superficie del campo effettivo gravitazionale, è continua e di forma sferoidale ma presenta continue ondulazioni in presenza di variazioni locali di densità dei materiali che compongono la crosta terrestre.
Questa particolare superficie prende il nome di geoide, che può essere ben definita da un mareografo. La sua superficie è complessa e difficilmente esprimibile con un'equazione.
- superficie ellissoidica o ellissoide di rotazione: introdotta come strumento matematico sul quale sviluppare in maniera analitica lo sviluppo della superficie effettiva.
Le coordinate geografiche, latitudine e longitudine, si riferiscono a questo tipo di superficie, in cui è necessario operare con i metodi della geometria sferica.
- campo geodetico di Weingarten o Sfera locale: sostituisce, nel massimo raggio di 100 km intorno a un punto, una sfera tangente all'ellissoide.
Campo topografico
Il campo topografico è la parte della superficie terrestre intorno a un punto, entro cui si può ritenere trascurabile l'errore di sfericità ai fini planimetrici ed entro cui è possibile, pertanto, eseguire un rilievo planimetrico senza commettere errori che influiscano sensibilmente sui risultati delle operazioni topografiche.
L'errore di sfericità che si commette nella misura delle distanze è pari a: . L'errore di sfericità che si commette nella misura dei dislivelli è pari a: in cui D è la distanza, R il raggio della terra, l'angolo al centro della sfera locale e 206.205 la misura in secondi sessagesimali di un radiante.
Il raggio del campo topografico si può estendere sino a 10 km circa quando si proceda a misure di distanza con precisione 1/1.000.000 (un millimetro su un chilometro). Nella grande maggioranza dei rilievi di estensione limitata è sufficiente la precisione di 1:200.000, con raggio del campo topografico sino a circa 25 km. Nel caso in cui si proceda al rilievo delle quote il campo topografico si riduce a poche centinaia di metri.
Cartografia e rappresentazione del terreno[modifica | modifica wikitesto]
Classificazione delle carte
- carte geografiche. scala inferiore a 1:1 000 000
- carte corografiche. scala compresa tra 1:100 000 e 1:1 000 000
- carte topografiche. scala compresa tra 1:10 000 e 1:100 000
- Piante o mappe: scala maggiore di 1:10 000
Rappresentazione dell'ellissoide sul piano
Le proiezioni cartografiche
Per proiezione cartografica si intende la tecnica di formazione di una carta ottenuta proiettando i punti dell'ellissoide su una superficie sviluppabile su un piano, quindi la proiezione diretta dei punti dell'ellissoide sul piano della carta per le proiezioni prospettiche, il cilindro per le proiezioni cilindriche e il cono per le proiezioni coniche.
- Proiezioni prospettiche
- Proiezioni cilindriche
- Proiezioni coniche
Le rappresentazioni cartografiche
Per rappresentazione cartografica si intende il metodo di rappresentazione piana di superficie generato per via puramente analitica imponendo solo alcune condizioni ai valori che possono assumere i parametri di deformazione lineare, areale e angolare.
- Rappresentazione sinusoidale di Sanson-Flamsteed
- Rappresentazione di Cassini-Soldner
- Rappresentazione di Gauss
- Rete di livellazione e rete geodetica italiana
- Carte dell'Istituto Geografico Militare
- Cartografia catastale
- Cartografia tecnica regionale
- Sistemi informativi territoriali (SIT)
- Cartografia numerica
Rappresentazione plani-altimetrica del terreno
- Proiezioni quotate
- Piani quotati
- Piani a curve di livello
Richiami di trigonometria piana[modifica | modifica wikitesto]

- Relazioni fra gli elementi di un triangolo rettangolo (con ):
e analoghe per rotazione
Triangolo qualunque
- Teorema dei seni e analoghe per rotazione
- Teorema del coseno o di Carnot e analoghe per rotazione
- Teorema delle tangenti o di Nepero ; ;
- Teorema delle cotangenti o di Viète: e analoghe per rotazione
- Formule di Briggs e analoghe per rotazione
- Formule dell'area: (Formula di Erone)
- Raggi cerchi notevoli: circoscritto ; inscritto ; ex-inscritto
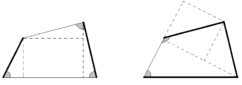
Le formule dei triangoli qualunque sopra riportate sono applicabili ognuna a seconda degli elementi noti che disponiamo del triangolo, o del quadrilatero o altro poligono riconducibile a una somma di triangoli mediante la scomposizione tramite diagonali.
Alcuni quadrilateri possono invece risultare di possibile risoluzione solo se scomposti in triangoli rettangoli e risolti come tali, come nel caso siano noti due lati opposti e tre angoli, o nel caso siano noti tre lati e i due angoli adiacenti al lato incognito.
Conversione di coordinate[modifica | modifica wikitesto]
Passaggio da coordinate cartesiane a coordinate polari con la funzione e riporto degli angoli al vero quadrante
1° quadrante + / + -------------> (AB) = (AB)*
2° quadrante + / - -------------> (AB) = π - (AB)*
3° quadrante - / - -------------> (AB) = π + (AB)*
4° quadrante - / + -------------> (AB) = 2π - (AB)*
Individuazione dei punti sul terreno[modifica | modifica wikitesto]
I segnali vanno dimensionati e posizionati in maniera da essere visibili alle distanze convenute a occhio nudo e, in alcuni casi, con il cannocchiale. È quindi necessario tenere presente che l'occhio umano possiede un'acuità visiva di 60", cioè può vedere un oggetto solo se appare entro un angolo visuale maggiore o uguale a 60".
Considerando l'altezza d dell'oggetto come l'archetto di una circonferenza di raggio pari alla distanza D dell'oggetto dall'occhio, ed = 60", questa può essere calcolata con l'espressione ed essendo = 60" e = 206.265" si ha che: d = 0,0003*D. Se invece si utilizza un occhiale di ingrandimento I, d = 0,0003*D/I
Segnali provvisori
- Chiodi, picchetti, paline, biffe, paloni, mire luminose, segnali aerofotogrammetrici
Segnali permanenti
- Capre, elioscopi, segnali luminosi, fotocellule, elementi di costruzione, vertici trigonometrici, vertici e punti fiduciali catastali.
Monografie e allineamenti servono invece per la ricerca indiretta dei punti, qualora risultino sconosciuti o di difficile individuazione.
Inserimento dei punti rilevati nel sistema cartografico[modifica | modifica wikitesto]
L'inserimento del punti rilevati nel sistema cartografico (georeferenziazione) consiste essenzialmente in una rototraslazione dei punti del rilievo sugli omologhi cartografici, ossìa in una sovrapposizione del rilievo sulla cartografia, o in taluni casi del rilievo sul rilievo che ha generato la cartografia. I punti omologhi utilizzati per la rototraslazione sono in genere punti di coordinate note aventi il maggiore grado di attendibilità fra quelli utilizzati e presenti sul territorio,
- Metodi di rototraslazione
- Rototraslazione baricentrica con e senza adattamento di scala
- Rototraslazione orientata con e senza adattamento di scala
- Rototraslazione ai minimi quadrati con e senza adattamento di scala
- Apertura a terra semplice e multipla
Strumenti topografici[1][2][modifica | modifica wikitesto]
Strumenti semplici
Supporti degli strumenti
- Bastone per squadro agrimensorio, Treppiede a perno, Treppiede a gambe intere e rientrabili, Treppiede a testa sferica e Treppiede centrante.
Strumenti per la verifica della verticalità e/o l'orizzontalità, o la misura di angoli
- Filo a piombo
- Piombino a bastone: Detto anche bastone telescopico è formato da due aste telescopiche con l'asta esterna graduata, terminante a punta e corredato di livella sferica. Montato sul treppiede permette di leggere l'altezza strumentale nel punto di stazione.
- Piombino ottico: Costituito da un piccolo cannocchiale ad angolo retto con un prisma a riflessione totale è montato su quasi tutti i basamenti dei tacheometri e dei teodoliti. È possibile rendere verticale l'asse del cannocchiale inferiore, solidamente all'asse di rotazione dello strumento, tramite tre viti calanti e una livella sferica montate sul basamento.
- Archipendolo
- Livella sferica
- Livella torica
- Squadro agrimensorio
- Bussole topografiche: Si tratta di goniometri azimutali che misurano l'azimut magnetico, da cui, conoscendo la declinazione magnetica, è possibile dedurre l'azimut geografico; sono costituite da un cerchio orizzontale graduato con il centro coincidente con il fulcro dell'ago magnetico, e una mira per la collimazione del punto.
Strumenti per la mira
- Paline, squadro agrimensorio
- Diottra a traguardi: Formata da una riga metallica con alle estremità due alette metalliche piegabili con fenditure verticali, oppure una con i fili incrociati, permette di ottenere una linea di mira disposta su un piano e quindi si può realizzare un allineamento di paline verticali.
Strumenti per la misura delle distanze
- Rotella metrica o doppio decametro
- Flessometro
- Metro ripiegabile
- Triplometro
- Odometro
Strumenti ottici
A riflessione
- Squadro a specchi
- Squadro a specchi di Adams
- Squadro allineatore a specchi
- Croce di specchi
Costruzione geometrica del raggio rifratto: dove r = raggio rifratto, i = raggio incidente, n = indice di rifrazione
Teorema di Jadanza: Quando un raggio luminoso entra in un prisma dalla faccia di incidenza ed esce dalla faccia di emergenza dopo avere subito all'interno del prisma due riflessioni su due facce diverse da quelle di incidenza ed emergenza, il raggio emergente risulta deviato rispetto a quello incidente di un angolo uguale a quello formato dalle facce di incidenza ed emergenza, purché risulti: , se è acuto, essendo l'angolo formato dalle due facce riflettenti; , se è ottuso.
- Prisma triangolare retto
- Squadro a prisma triangolare di Bauernfeind
- Squadro a prisma di Wollaston
- Prisma allineatore di Porro
- Prisma squadro di Zeiss
- Prisma universale di Jadanza
- Prisma squadro e allineatore di Bauernfeind
- Croci di prismi
- Squadro allineatore a specchi di Coutureau
Diottrici
- Occhio umano
- Microscopio semplice e composto
- Cannocchiali
- Cannocchiale astronomico (o di Keplero)
- Cannocchiale a lunghezza costante
- Cannocchiale terrestre
- Cannocchiale di Galileo
- Cannocchiale a prisma
- Cannocchiale con prisma a tetto
- Cannocchiale catadiottrico
Strumenti per la misura degli angoli o Goniometri
Con il termine goniometro si indicano in generale tutti gli strumenti per la misurazione degli angoli. Dal greco gonios = angolo e metron = misura. I goniometri usati in topografia (classificati in base al metodo con cui individuano le direzioni o al tipo di angoli che possono misurare) sono:
- Azimutali Strumenti a cerchi graduati con o senza lettura al nonio o al microscopio utilizzati per la misura degli angoli orizzontali. Il nome deriva da azimut, l'angolo diedro avente come spigolo la verticale del luogo (la normale) e per facce i piani passanti per un astro e un punto all'infinito.
- A traguardi
- A prisma
- A cannocchiale, come il tacheometro e il teodolite
- Zenitali Strumenti a cerchi graduati con o senza lettura al nonio o al microscopio utilizzati per la misura degli angoli verticali.
- Ecclimetri Strumenti a cannocchiale dotati di cerchio verticale graduato. L'ecclimetro è il cerchio verticale nel tacheometro e nel teodolite.
- Clisimetri Strumenti a cannocchiale utilizzati per la misura delle pendenze che invece del cerchio graduato sono provvisti di una scala delle pendenze, in cui si legge la tangente dell'angolo della visuale. La graduazione, espressa in percentuale, fornisce il dislivello fra due punti distanti 100 m. I clisimetri possono essere a cannocchiale o a visione naturale, come i clisimetri a traguardi, a sospensione e a riflessione.
- Sestanti
- Azimutali e zenitali
- Mediante squadro agrimensorio, bussola topografica e livella torica
Strumenti per la misura delle distanze
Strumenti di misura diretta
- Rotella metrica o doppio decametro, Flessometro, Metro ripiegabile, Odometro, Triplometro
- Nastri d'acciaio
- Apparato di Jaderin
Strumenti di misura indiretta
- Distanziometri a onde
- Distanziometri a laser
- Distanziometri a prisma
- Telemetri Il telemetro consiste in un'asta con lunghezza nota b, (o anche variabile nel caso di telemetro a base variabile) alle cui estremità sono montati due cannocchiali, di cui uno con l'asse retto rispetto all'asta, in A, e l'altro, in B, libero di ruotare intorno al suo asse verticale, dotato di cerchio orizzontale che permette di leggere l'angolo rispetto al punto P collimato. La distanza è calcolabile risolvendo il triangolo ABP, in cui l'angolo letto esterno al triangolo, è anche l'angolo interno:
- Strumenti autoriduttori. Nelle misure con stadia verticale, i cannocchiali con reticolo autoriduttore fanno variare l'angolo parallattico in modo che, qualunque sia l'inclinazione dell'asse di collimazione ( variazione nel caso di cannocchiale ad angolo parallattico costante) la differenza delle letture ai fili S rimanga costante.
- Mediante stadia e cannocchiale distanziometrico
- stadia verticale e cannocchiale ad angolo parallattico costante:
Dato che , in cui r = distanza tra i fili estremi del micrometro; f = distanza focale dell'obiettivo; S = (l1 - l2) = intervallo di stadia letto ai fili distanziometrici del reticolo; D = distanza fra il punto anallattico e la stadia. r / f = k = costante diastimometrica o distanziometrica [pari a 50, 100 o 200], si ha che:
- con asse di collimazione orizzontale . con c = e + f, [35-50 cm], e = distanza fra i centri strumentale e lente obiettivo, f = distanza focale dell'obiettivo
- con asse di collimazione inclinato con
- stadia verticale e cannocchiale ad angolo parallattico variabile, con asse di collimazione anche inclinato
- stadia orizzontale e cannocchiale ad angolo parallattico costante, con asse di collimazione anche inclinato
- stadia orizzontale e cannocchiale ad angolo parallattico variabile, con asse di collimazione anche inclinato
- Mediante ecclimetri
- Mediante clisimetri
Strumenti per la misura dei dislivelli
- Mareografi
- Barometri
- Livelli idrostatici
Con mire e stadie
- Livelli a cannocchiale
- Livelli a visuale reciproca
- Livelli a manicotto
- Livelli autolivellanti
- Livelli a laser rotante
- Livelli digitali
- Livelli zenitali e nadirali
- Livelli a traguardi
- Ecclimetri e clisimetri
- Triplometro
Stazioni totali

La stazione totale è uno strumento computerizzato che oltre ad assolvere la classica funzione di teodolite (cioè misuratore di angoli orizzontali e verticali) unisce un elettrodistanziometro (EDM), cioè un ricetrasmettitore di raggi infrarossi o laser. Nel primo caso è indispensabile un riflettore e quindi un operatore ausiliario chiamato canneggiatore, nel secondo caso è sufficiente qualsiasi superficie e quindi è possibile effettuare misurazioni anche soli con lo strumento. L'EDM valuta la distanza tra due punti misurando la differenza di fase tra un'onda sinusoidale emessa e ricevuta (EDM a differenza di fase) oppure il tempo impiegato dall'onda emessa dallo strumento per eseguire il percorso (EDM a impulsi). L'EDM invia un segnale modulato a dei particolari prismi ottici a 45º (posizionati su appositi sostegni nei punti da rilevare) che li riflettono verso l'unità base. Quest'ultima è dotata di un fasometro il quale calcola indirettamente la distanza inclinata per via di successive approssimazioni. In genere al fasometro è accoppiato un computer il quale può fornire la distanza in piano previo inserimento dell'angolo verticale.
Il GPS nelle applicazioni topografiche
Il GPS viene utilizzato anche frequentemente per scopi topografici/cartografici. In genere per le applicazioni topografiche, dove le precisioni richieste sono di tipo centimetrico, non si utilizzano le normali tecniche di rilievo GPS utilizzate per la navigazione. La tecnica più diffusa è quella della misura in differenziale. Essendo la differenza tra il valore delle reali coordinate del punto e quelle rilevate dallo strumento GPS, variabili nel tempo ma costanti a livello locale, è possibile operare con due strumenti in contemporanea. Uno, il master, verrà localizzato su un punto noto nei pressi del punto da rilevare. L'altro, il rover, effettuerà il rilievo. Avendo, attraverso il master, la registrazione dell'errore locale, istante per istante, le letture del rover verranno corrette attraverso queste ottenendo precisioni fino a 2 ppm, ovvero 1 millimetro su un chilometro.
Metodi di rilievo[1][2][modifica | modifica wikitesto]
Rilevamento altimetrico: misura dei dislivelli[modifica | modifica wikitesto]
Nelle seguenti formule per h si intende l'altezza strumentale nel punto di osservazione, per l la lettura, o l'altezza strumentale nel punto osservato, per R il raggio della terra, per k l'indice di rifrazione atmosferica, (per l'Italia 0,12 - 0,14 da sud a nord) e per l'angolo zenitale apparente misurato nel punto di stazione.
Livellazione geometrica[modifica | modifica wikitesto]
Nella livellazione geometrica l'asse di collimazione è orizzontale, le distanze fra i punti non superano in genere 70-80 m, e sono del tutto trascurabili gli errori di sfericità e rifrazione.
- Livellazione geometrica da un estremo
- Livellazione geometrica dal mezzo
- Livellazione geometrica reciproca , e, calcolando l'errore è inoltre possibile effettuare la rettifica del livello
- Livellazione geometrica composta
Livellazioni a visuale libera[modifica | modifica wikitesto]
- Livellazione trigonometrica reciproca Hm: quota media tra A e B calcolata in prima approssimazione ponendo Hm=HA
- Livellazione trigonometrica da un estremo
- Calcolo della quota di un punto A dal quale è visibile l'orizzonte marino
- Problema del faro: distanza D di un punto dell'orizzonte marino dal quale è visibile un faro alla quota HA = QA + hA: o, problema inverso, l'altezza hA che deve avere un faro posto nel punto A, di quota nota QA, affinché sia visibile dalla distanza D prefissata:
Livellazioni senza visuali[modifica | modifica wikitesto]
- Livellazione barometrica
- Livellazione idrostatica
- Livellazione per coltellazione
Rilevamento planimetrico[modifica | modifica wikitesto]
Rilievo per intersezione[1][modifica | modifica wikitesto]
I metodi di intersezione formulati prevedono di stazionare direttamente sui punti di coordinate note, o che i punti siano reciprocamente visibili. Ciò nella pratica è difficilmente attuabile e pertanto il collegamento tra punti avviene in realtà mediante l'inserimento di poligonali.
- INTERSEZIONE IN AVANTI SEMPLICE E MULTIPLA
Permette di determinare le coordinate planimetriche di un punto P inaccessibile, ma visibile da due punti di coordinate note A e B, accessibili e reciprocamente visibili
elementi noti:

;
Per verifica le coordinate di P possono essere calcolate in modo analogo anche rispetto a B.
Nell'intersezione in avanti multipla il procedimento descritto viene ulteriormente reiterato su altri punti di coordinate note e le coordinate di P si calcolano come media aritmetica dei risultati ottenuti.
- INTERSEZIONE LATERALE SEMPLICE E MULTIPLA
Permette di determinare le coordinate planimetriche di un punto P accessibile, e visibile da due punti di coordinate note A e B, dei quali solo uno è accessibile.
Il procedimento di risoluzione è del tutto simile all'intersezione in avanti.
- INTERSEZIONE INVERSA

Metodo di Snellius-Pothenot
Permette di determinare le coordinate planimetriche di un punto di stazione P dal quale sono visibili tre punti di coordinate note A, B e C
elementi noti:
;
Per verifica le coordinate di P possono essere calcolate in modo analogo anche rispetto a B e C.
Metodo di Cassini
- METODO DI HANSEN O DELLA DOPPIA INTERSEZIONE INVERSA
Consente di determinare le coordinate planimetriche di un punto di stazione M e una stazione ausiliaria N dai quali sono visibili due punti di coordinate note A e B.

Elementi noti:
Gli altri elementi finalizzati al calcolo delle coordinate di M e N si risolvono in maniera analoga agli altri metodi di intersezione.
- Metodo della base fittizia
Si fissa una base fittizia p.e. MN = 100 m, e si calcolano così gli angoli x e y. A questo punto si calcola la distanza reale AB e impostando il criterio di similitudine fra i triangoli ABM (incognito) e A'B'M' (quello calcolato con la base fittizia), si addiviene al valore della distanza reale AM. In modo analogo si considera il triangolo ABN per determinare AN. Infine vengono determinate le coordinate di M e N. Queste ultime possono essere calcolate anche come media delle coordinate relative ad A e B.
- Doppia intersezione in avanti
Poligonazioni[modifica | modifica wikitesto]
Il rilievo per poligonazione consiste nel collegare i punti di appoggio del rilievo tramite una spezzata detta poligonale, che può essere chiusa o aperta a seconda che i vertici iniziale e finale coincidano o meno.
Le poligonali chiuse si riducono a un poligono e pertanto l'errore di chiusura angolare viene compensato con la somma degli angoli interni: π(n - 2). Le poligonali aperte possono essere semplici o vincolate agli estremi a punti di coordinate note.
Nel caso di appoggio a punti di coordinate note è possibile effettuare la compensazione degli errori di chiusura angolare e lineare. In ogni caso si deve verificare la tolleranza rispetto ai limiti normativi.
Agrimensura[1][modifica | modifica wikitesto]
L'agrimensura è la parte della topografia che comprende i metodi di calcolo per la misura e il calcolo delle aree, per la divisione dei terreni e per la rettifica e lo spostamento dei confini. Si avvale di metodi grafici, di metodi numerici, di metodi grafo-numerici e di metodi meccanici. In ogni caso qualsiasi figura geometrica viene scomposta in figure elementari.
Misura e calcolo delle aree[modifica | modifica wikitesto]
Divisione delle aree[modifica | modifica wikitesto]
Superfici di uguale valore unitario
Sia da dividere un appezzamento triangolare ABC in tre parti, uguali o proporzionali ai numeri m1, m2 e m3. Dopo avere determinato l'area totale e le aree S1, S2 e S3, dalla formula dell'area si ricava , e con riferimento al triangolo ABE da si ricava
Le due distanze AD e AE possono anche essere calcolate osservando che i triangoli hanno la medesima altezza, pertanto le aree sono proporzionali alle basi e valgono le seguenti relazioni: [AD : S1 = AC : S] e [AE : (S1 + S2) = AC : S, dalle quali si ricavano: AD = (S1/S)*AC, e AE = [(S1+S2)/S]*AC.
- Superficie triangolare con dividenti uscenti da un punto P situato su un lato. Si procede in maniera analoga
- Superficie triangolare con dividenti uscenti da un punto P interno all'appezzamento. Si procede in maniera analoga
- Superficie triangolare con dividenti parallele a una direzione stabilita
La posizione delle dividenti MN e PQ viene determinata osservando che i triangoli ABC, MBN e PBQ sono simili e quindi dalle proporzioni relative si ricavano i lati cercati:
, si procede in maniera analoga per QB, e allo stesso modo, considerando i triangoli S1+S2 si calcolano MB e NB.
Spianamenti[modifica | modifica wikitesto]
Generalità[modifica | modifica wikitesto]
Nella pratica degli spianamenti il piano secondo il quale verrà sistemato il terreno è detto piano di progetto; le differenze fra quote di progetto e quote del terreno vengono chiamate quote rosse, corrispondenti materialmente all'altezza di scavo o di riporto praticata dai mezzi d'opera meccanici.
- PUNTO DI PASSAGGIO FRA LIVELLETTE
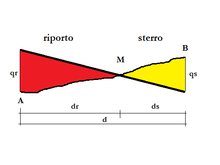
In una sezione generica verticale l'intersezione fra il profilo originario del terreno e il piano di spianamento, o di progetto, è detta punto di passaggio, che separa le superfici di scavo da quelle di riporto. Le quote di scavo e di riporto, o quote rosse, permettono di calcolare i relativi volumi.
incognite: quota di sterro in B; quota di riporto in A; distanza fra A e B
- CALCOLO DEI VOLUMI

Il volume del prismoide e del cilindroide non retto a basi parallele viene calcolato con la formula di Torricelli:
Per i volumi di terra è sufficiente porre con accettabile approssimazione: che sostituita nella formula precedente fornisce:
che viene detta formula delle sezioni ragguagliate maggiormente usata nella progettazione stradale per il calcolo del volume dei solidi fra due sezioni consecutive.
Il volume del prisma retto con le basi oblique, viene calcolato considerando che l'altezza da considerare è la distanza fra i baricentri delle facce. In un triangolo obliquo rispetto al piano di riferimento l'altezza del baricentro è la media delle altezze dei vertici; in tal caso la formula del volume estendibile anche a un prisma che ha come base un parallelogramma, è la seguente

con Area della sezione normale
maggiormente usata per il calcolo del volume dei solidi individuati da un piano quotato a maglia triangolare nelle operazioni di spianamento.
Spianamento con piano orizzontale di compenso[modifica | modifica wikitesto]
Si fissa una quota di progetto fittizia corrispondente a una quota più bassa della quota più bassa del terreno, pertanto se ne calcolano le quote rosse fittizie e i relativi volumi:
valida per tutti i vertici;

valida per tutte le superfici, e calcolo del volume totale fittizio
determinazione dell'altezza fittizia:
determinazione della quota di progetto, o di compenso: e delle reali quote rosse:
.
Determinazione dei punti di passaggio E e F (quote rosse nulle) mediante la loro distanza dai vertici.
Calcolo dei volumi di sterro e riporto ripetendo l'operazione effettuata con le quote rosse fittizie, tenendo presente che i prismi da assumere per il calcolo sono ora quelli individuati dai triangoli AEF, EFD, EBD e BCD.
Progettazione stradale[1][modifica | modifica wikitesto]
Sviluppo del progetto[modifica | modifica wikitesto]
- Studio del tracciato e planimetria
- Profilo longitudinale e livellette di compenso
- Il calcolo delle sezioni stradali

Sezioni trasversali
Intersezioni stradali[modifica | modifica wikitesto]
Due o più strade attraversandosi determinano un'intersezione. Le intersezioni possono essere libere, in cui il triangolo di visibilità è proporzionato alla distanza di visibilità per l'arresto, o regolate con segnali di precedenza e di arresto. Possono inoltre essere con o senza corsie di accelerazione e decelerazione.
- Intersezioni a raso o a livello,
- Intersezione semplice a tre rami
- Intersezione a tre rami canalizzate
- Intersezione a tre rami con allargamento di carreggiata
- Intersezione a quattro rami
- Intersezione a circolazione rotatoria
- Intersezioni a livelli sfalsati o a svincoli
Movimenti di terra[modifica | modifica wikitesto]
Oltre alla formula delle sezioni ragguagliate, per i tratti in curva, il solido stradale viene calcolato dal 2° Teorema di Guldino, con la formula che segue: dove A è l'area della sezione, d lo sviluppo dell'arco descritto dal baricentro della sezione, a la distanza del baricentro all'asse della sezione, R il raggio della curva.

- Diagramma dei volumi o profilo delle aree - Dalle sezioni trasversali relative a un determinato tronco si ottiene, calcolando il volume tra due sezioni successive con la formula delle sezioni ragguagliate, o per i tratti in curva la formula dal 2° Teorema di Guldino, il diagramma dei volumi, in quanto l'area compresa fra la spezzata e la fondamentale esprime il volume di scavo. Sull'orizzontale vanno riportate le distanze fra le sezioni e sulle ordinate le aree delle sezioni trasversali, collegando le ordinate rappresentanti le sezioni di una stessa parzializzazione. Tale grafico viene detto anche profilo delle aree poiché la spezzata si ottiene unendo le estremità delle ordinate che rappresentano le aree delle sezioni. L'andamento lineare del grafico è dovuto all'uso della formula delle sezioni ragguagliate. Le aree di scavo vanno moltiplicate per una percentuale di rigonfiamento prima di essere considerate nell'eseguire il diagramma.

- Diagramma dei volumi depurato dei compensi trasversali - Poiché il costo dei movimenti di terra dipende essenzialmente dagli spostamenti effettuati nel senso longitudinale, dal diagramma dei volumi vengono eliminati quei volumi che verranno spostati nel senso trasversale, mediante compenso trasversale delle aree. Questa operazione è denominata paleggio.

- Diagramma dei volumi eccedenti o di Brückner
- Distanza media di trasporto e momento di trasporto Dal Diagramma di Brückner si ricava l'ordinata finale della spezzata integrale che, letta nella scala delle distanze, fornisce la distanza media di trasporto in orizzontale Dm. Nel caso di percorso in salita Dm si moltiplica per (1+n*p), in cui n va da 10 a 20 per trasporto con ruspa, e da 25 a 40 per trasporto con autocarro e p è la pendenza del percorso. Sempre dal Diagramma di Brückner si ricava l'ordinata massima del cantiere Ymax = V, ossia il volume che, moltiplicato per la distanza media Dm fornisce il momento di trasporto , uguale all'area compresa fra la curva e la fondamentale, e sommatoria dei volumi elementari per le distanze alle quali devono essere trasportati.
- Costo dei trasporti in cui k = costo unitario; = peso volumico terra
- Fondamentale di minima spesa
- Zona di occupazione - Espropriazioni
Note[modifica | modifica wikitesto]
Bibliografia[modifica | modifica wikitesto]
- R. Accademia di Fanteria e Cavalleria, Sinossi di Topografia Militare, Stabilimento Poligrafico Modenese, 1930 (IX). compilate dal Maggiore Ercole Barbero, insegnante titolare di Topografia presso la R. Accademia fi Fanteria e Cavalleria, ad uso esclusivo della R. Accademia e fuori commercio
- Istuituto Geografico Militare, Pubblicazioni Varie
- R. Barbetta, Topografia pratica.
- Col. Cavicchi, Norme per il rilevamento speditivo.
- Col. Redi, Norme pratiche per determinazioni speditive della posizione geografica.
Voci correlate[modifica | modifica wikitesto]
- Soluzione automatica dei poligoni con il P.C.
- Aerofotogrammetria
- Carta topografica
- Cartografia
- Ellissoide di riferimento
- Fotogrammetria
- Geodesia
- Carta geografica
- Monografia (topografia)
- Percorso rettificato
- Proiezione cartografica
- Proiezione quotata
- Punto di riferimento
- Sistema informativo geografico
- Topografia antica
- Agronomo
- Ingegnere
- Architetto
- Geometra
- Perito agrario
Altri progetti[modifica | modifica wikitesto]
 Wikizionario contiene il lemma di dizionario «topografia»
Wikizionario contiene il lemma di dizionario «topografia» Wikimedia Commons contiene immagini o altri file su topografia
Wikimedia Commons contiene immagini o altri file su topografia
Collegamenti esterni[modifica | modifica wikitesto]
- (EN) topography / topography (altra versione), su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
- Facoltà di geomatica e geodesia al Politecnico di Milano
- Cattedra di Topografia dell'Università degli Studi di Brescia, su rilevamento.it.
- Fonti web per le scienze geodetiche
- Il trattamento delle osservazioni in topografia, su topografi.it (archiviato dall'url originale il 13 agosto 2007).
| Controllo di autorità | Thesaurus BNCF 5455 · LCCN (EN) sh85136077 · GND (DE) 4133697-5 · BNE (ES) XX4576245 (data) · J9U (EN, HE) 987007541319105171 |
|---|





















































![{\displaystyle [X_{A};Y_{A}]\qquad [X_{B};Y_{B}]\qquad [B{\widehat {A}}P]\qquad [P{\widehat {B}}A]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/edfed7f1e2937a792ae4f12437d7693dd0a4a244)






![{\displaystyle [X_{A};Y_{A}]\qquad [X_{B};Y_{B}]\qquad [X_{C};Y_{C}]\qquad [\alpha ]\qquad [\beta ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07356492ff3dd0da600c73ea4afeef7c078bca9d)




![{\displaystyle {\frac {x-y}{2}}=\arctan[\tan {\frac {x+y}{2}}\cdot \tan(\pi /4-\theta )];\qquad \theta =\arctan {\frac {AB\operatorname {sen} \beta }{BC\operatorname {sen} \alpha }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3285e6b8c8d07718e89ee862f346089ffa57327)




![{\displaystyle [X_{A};Y_{A}]\qquad [X_{B};Y_{B}]\qquad [\alpha ]\quad [\alpha _{1}]\qquad [\beta ]\quad [\beta _{1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d092d129258af50166bd8f28c94e7026a3376080)

![{\displaystyle {\frac {x-y}{2}}=\arctan[\tan {\frac {x+y}{2}}\cdot \tan(\pi /4-\theta )];\qquad \theta =\arctan {\frac {\operatorname {sen} \beta \cdot \operatorname {sen}(\alpha _{1}+\beta _{1})}{\operatorname {sen} \beta _{1}\cdot \operatorname {sen}(\alpha +\beta )}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/00af692ac033a2f29c06447d7f85d0151fafd932)






![{\displaystyle [q_{s}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b254cc69c05152bb03f8e17b557e6cabb6f13cce)
![{\displaystyle [q_{r}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2b48319553dbe4ad16a5684c0b1fe46ec23994b)
![{\displaystyle [d]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef4f4d84e860f2ffd5b55eec14cfbf735dd01689)


















