Imaging con tensore di diffusione
| Imaging con tensore di diffusione | |
|---|---|
Procedura diagnostica  Immagine ottenuta tramite tensore di diffusione | |
| Anestesia | No |
| MeSH | D056324 |
Il tensore di diffusione è uno strumento di risonanza magnetica attraverso il quale si possono costruire immagini biomediche (DTI, sigla dell'inglese Diffusion Tensor Imaging) anche tridimensionali, ma di tipo intrinseco.
Il tensore, cioè, usa il calcolo infinitesimale per definire nozioni geometriche di distanza, angolo e volume e studiare le curve di strutture anatomiche nelle quali una dimensione è di molto maggiore delle altre due (per esempio i fasci di fibre nervose della sostanza bianca).
Le molecole d'acqua in un tessuto biologico non sono libere di muoversi, a causa della presenza delle membrane biologiche e delle strutture cellulari e infracellulari, ma proprio per questo nel complesso si può osservare un'isotropia di tali movimenti: apparentemente, cioè, le molecole d'acqua non si muovono in una direzione particolare, ma lo fanno nella medesima misura in tutte e tre le direzioni.
Invece strutture anatomiche omogenee, come possono essere i fasci di fibre nervose, presentano un'anisotropia, cioè una peculiare direzionalità che si riflette nella diffusione delle molecole d'acqua e che viene per l'appunto sfruttata per creare le immagini 3D del DTI.
Tecnica[modifica | modifica wikitesto]
Occorrono come minimo 6 acquisizioni pesate in DWI per ottenere un'immagine DTI.
Questa deriva l'informazione direzionale dei tratti neurali da più dati provenienti dallo stesso voxel, servendosi di algoritmi 3D o di vettore multidimensionale basandosi su tre, sei, o più direzioni di gradiente, sufficienti per elaborare il tensore di diffusione. Il modello di diffusione è un modello piuttosto semplice del processo di diffusione, che assume l'omogeneità e la linearità della diffusione all'interno di ogni voxel d'immagine. Dal tensore di diffusione, tramite elaborazione si ricavano misure dell'anisotropia di diffusione come l'anisotropia frazionale (FA). Inoltre la principale direzione del tensore di diffusione può essere usato per inferire la connettività della materia bianca del cervello (ad.es. nella trattografia per determinare quale porzione del cervello è connessa con un'altra parte).
Recentemente, sono stati proposti modelli più avanzati del processo di diffusione, con lo scopo di superare la debolezza del modello matematico del tensore di diffusione. Tra gli altri, questi includono il "Q-Space Imaging"[1][2][3] e l'imaging generalizzato del tensore di diffusione ("generalized diffusion tensor imaging").
Come si descrive[modifica | modifica wikitesto]
Lo strumento matematico che descrive la distribuzione della diffusione in 3D è il Tensore di diffusione, che altro non è che una matrice 3x3 simmetrica (6 parametri indipendenti).
Si tratta di associare ad ogni punto dello spazio un tensore, aumentando il numero dei parametri associati ad ogni posizione. Per acquisire immagini sensibili agli effetti di diffusione occorre introdurre nella sequenza di acquisizione dei gradienti di campo magnetico ad hoc.
Equazione di Bloch–Torrey[modifica | modifica wikitesto]
Nel 1956, H.C. Torrey dimostrò matematicamente come le equazioni di Bloch per la magnetizzazione cambino con l'aggiunta delle diffusione.[4] Torrey modificò la descrizione originale della magnetizzazione trasversa fatta da Bloch, in modo da includere i termini di diffusione e l'applicazione di un gradiente spazialmente variante.
L'equazione di Bloch-Torrey (tralasciando il rilassamento) è:
Per il caso più semplice dove la diffusione è isotropica, il tensore di diffusione equivale a
il che significa che l'equazione di Bloch–Torrey avrà la soluzione
Questo dimostra una dipendenza cubica della magnetizzazione trasversa dal tempo. La diffusione anisotropica avrà un metodo di soluzione simile, ma con un tensore di diffusione più complesso.
Applicazioni[modifica | modifica wikitesto]
Le principali applicazioni sono quelle nella visualizzazione della sostanza bianca, per determinare la localizzazione, orientamento, e anisotropia dei tratti e dei fasci di fibre nervose. L'architettura dei gruppi di assoni in fasci paralleli e le loro guaine di mielina, facilitano la diffusione delle molecole d'acqua preferenzialmente lungo la loro principale direttrice. Questa diffusione orientata viene chiamata diffusione anisotropica (dall'inglese: anisotropic diffusion).
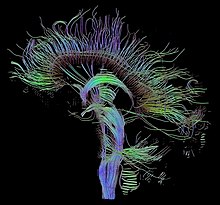
La visualizzazione (imaging) di questa proprietà della materia bianca è una estensione della RM a diffusione. Se vengono applicati una serie di gradienti di diffusione (cioè variazioni del campo magnetico nel magnete della RMI) in maniera che possano fornire almeno 3 vettori direzionali (l'utilizzo di 6 diversi gradienti è il minimo indispensabile e gradienti addizionali migliorano l'accuratezza per l'informazione "diagonale"), è possibile calcolare, per ogni voxel, un tensore (cioè definire una matrice simmetrica positiva) che descrive la forma tridimensionale della diffusione delle molecole d'acqua. La direzione delle fibre viene indicata dall'autovettore principale del tensore. Questo vettore può ricevere una codifica a falsi colori, fornendo così una cartografia della posizione e direzione dei tratti (rosso per sinistra-destra, blu per superiore-inferiore, e verde per anteriore-posteriore). La brillantezza viene pesata dall'anisotropia frazionale che è una misura scalare del grado di anisotropia in un dato voxel. La "diffusività media" (in inglese "Mean diffusivity" o MD) oppure traccia è una misura scalare della diffusione totale all'interno di un voxel. Queste misure vengono spesso usate nella clinica per localizzare lesioni della sostanza bianca che non si evidenziano in altre forme di Imaging a Risonanza Magnetica clinica.
I dati provenienti dall'imaging del tensore di diffusione possono essere usati per eseguire la trattografia all'interno della sostanza bianca. Algoritmi per il rilevamento delle fibre possono essere usati per ricostruire il tracciato di una fibra lungo la sua intera lunghezza (ad.es. il tratto corticospinale, che invia gli impulsi dei neuroni motori dalla corteccia motoria fino ai motoneuroni delle corna anteriori del midollo spinale). La trattografia è un metodo utile per misurare i deficit nella materia bianca, come quelli dovuti alle malattie demielinizzanti (adrenoleucodistrofia, SLA, SM) oppure dall'invecchiamento. Le sue stime dell'orientamento e della forza delle fibre sono incredibilmente accurate, ed hanno ampie implicazioni potenziali nel campo della neuroscienza e neurobiologia cognitiva[5].
Alcune tra le applicazioni cliniche della DTI sono nella localizzazione tratto-specifica delle lesioni della sostanza bianca come vari tipi di trauma e nello stabilire la severità del danno traumatico cerebrale diffuso. La localizzazione del tumore in rapporto ai tratti di materia bianca (infiltrazione, deflessione), è stata una delle più importanti applicazioni iniziali. Nella pianificazione di interventi chirurgici per alcuni tipi di tumore al cervello, la neurochirurgia viene aiutata dalla conoscenza della prossimità e posizione relativa del tratto corticospinale rispetto al tumore.
L'utilizzo della DTI per stabilire il ruolo della sostanza bianca nello sviluppo, patologia e degenerazione è stato il punto focale di più di 2.500 lavori di ricerca sin dal 2005. La tecnica della DTI promette essere molto utile nel distinguere il malattia di Alzheimer da altri tipi di demenza. Le applicazioni nella ricerca sul cervello coprono ad. es. l'investigazione della connettività delle reti neurali in vivo.[6]
La DTI ha anche applicazioni nell'investigazione del muscolo scheletrico e del muscolo cardiaco. La sensitività all'orientamento delle fibre sembra essere d'aiuto anche nell'arena della medicina dello sport dove aiuta molto l'imaging della struttura e delle lesioni ai muscoli e tendini.
Una ricerca recente nello Barnes-Jewish Hospital e nella Washington University School of Medicine che studiava sia persone in salute che individui affetti da neurite ottica, malati da poco tempo ma anche cronici (neurite che spesso è il sintomo d'esordio della sclerosi multipla), mostrava che la DTI può essere impiegata per misurare il progredire degli effetti di questa malattia sul nervo ottico e dunque sulla visione, perché misura la diffusività assiale dell'acqua nell'area.
Alterazioni della sostanza bianca dovute all'esercizio[modifica | modifica wikitesto]
Nell'ottobre del 2009 venne pubblicata una ricerca che documentava un incremento localizzato della anisotropia frazionale in seguito all'addestramento a un complesso compito visivo-motorio (la giocoleria). Nella pubblicazione si sosteneva che si tratti della prima evidenza di cambiamenti dovuti all'esperienza nella microstruttura della sostanza bianca in esseri umani adulti sani.[7]
Note[modifica | modifica wikitesto]
- ^ HARDI/Q-Space Imaging
- ^ q-Space imaging correlates with mechanical strain
- ^ q-Space imaging of the brain
- ^ H. C. Torrey, Bloch Equations with Diffusion Terms, in Physical Review, vol. 104, 1956, p. 563, Bibcode:1956PhRv..104..563T, DOI:10.1103/PhysRev.104.563.
- ^ (EN) Marco Catani e Michel Thiebaut de Schotten, Atlas of Human Brain Connections, OUP Oxford, 14 giugno 2012, ISBN 978-0-19-954116-4. URL consultato il 10 dicembre 2022.
- ^ L. Minati, D. Aquino, Probing neural connectivity through Diffusion Tensor Imaging (DTI), In: R. Trappl (Ed.) Cybernetics and Systems 2006:263-68, 2006
- ^ Jan Scholz, Miriam C Klein, Timothy E J Behrens e Heidi Johansen-Berg, Training induces changes in white-matter architecture, in Nature Neuroscience, vol. 12, n. 11, --, pp. 1370–1371, DOI:10.1038/nn.2412, ISSN 1097-6256,1546-1726, PMC 2770457, PMID 19820707.
Voci correlate[modifica | modifica wikitesto]
- Imaging a risonanza magnetica
- Diffusione (RMN)
- Diffusione molecolare
- Moto browniano
- Tensore
- Calcolo tensoriale
- Geometria differenziale
- Geometria differenziale delle curve
Altri progetti[modifica | modifica wikitesto]
 Wikimedia Commons contiene immagini o altri file su Imaging con tensore di diffusione
Wikimedia Commons contiene immagini o altri file su Imaging con tensore di diffusione
Collegamenti esterni[modifica | modifica wikitesto]
| Controllo di autorità | LCCN (EN) sh2005006795 · BNF (FR) cb151239208 (data) · J9U (EN, HE) 987007530663705171 |
|---|


