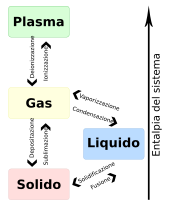
Gas ideale

Un gas ideale, o gas perfetto[1][2], è un gas descritto dall'equazione di stato dei gas perfetti, e che quindi rispetta la legge di Boyle-Mariotte, la prima legge di Gay-Lussac o legge di Charles, e la seconda legge di Gay-Lussac, in tutte le condizioni di temperatura, densità e pressione.[3][4][5] In questo modello le molecole del gas sono assunte puntiformi e non interagenti. I gas reali si comportano con buona approssimazione come gas perfetti quando la pressione è sufficientemente bassa e la temperatura sufficientemente alta.[6]
Proprietà di un gas ideale[modifica | modifica wikitesto]
Per gas ideale si intende un gas che possieda le seguenti proprietà:[7]
- le molecole sono puntiformi e pertanto hanno un volume trascurabile;
- le molecole interagiscono tra loro e con le pareti del recipiente mediante urti perfettamente elastici (ovvero non vi è dispersione di energia cinetica durante gli urti);
- non esistono forze di interazione a distanza tra le molecole del gas: le molecole si dicono "non interagenti";
- le molecole del gas sono identiche tra loro e indistinguibili;
- il moto delle molecole è casuale e disordinato in ogni direzione, ma soggetto a leggi deterministiche.
In conseguenza di ciò:
- il gas non può essere liquefatto per sola compressione, ossia non subisce trasformazioni di stato;
- il calore specifico è funzione della temperatura;
- l'energia interna è data solamente dall'energia cinetica, non da quella potenziale; essa rimane costante e non viene dissipata.
In un gas ideale l'energia cinetica media delle molecole del gas è direttamente proporzionale alla temperatura:
I gas reali vengono descritti dalla legge dei gas perfetti con buona approssimazione solo quando la pressione è sufficientemente bassa e la temperatura sufficientemente alta. In caso contrario è valida la legge dei gas reali.
Energia interna[modifica | modifica wikitesto]
La variazione dell'energia interna è una funzione di stato, ossia ha la proprietà di dipendere solo dal suo stato iniziale e finale e non dal percorso compiuto. In generale l'energia interna è una funzione sia della temperatura che del volume, differenziando si ottiene quindi:
Considerando i risultati matematici dell'esperienza di Joule per l'espansione libera di un gas perfetto:
e sostituendo nel differenziale precedentemente calcolato, si ottiene:
Ovvero per i gas perfetti l'energia interna è funzione solamente della temperatura.[8]
Definendo come la capacità termica a volume costante, allora per una trasformazione isocora dal primo principio della termodinamica si ha che:
dove è il calore scambiato dal gas con l'ambiente durante la trasformazione. Assumendo che la capacità termica è costante con la temperatura, e usando la legge dei gas perfetti, allora il primo principio della termodinamica può essere riscritto per i gas ideali e per trasformazioni quasistatiche come
dove è la costante universale dei gas e è il numero di moli di gas.[9]
Entropia[modifica | modifica wikitesto]
Si consideri una trasformazione reversibile che porti moli di gas perfetto da uno stato con pressione, volume e temperatura ad uno stato finale . La quantità infinitesima di calore scambiata nella trasformazione è data da:
dove è il calore specifico a volume costante.
Ricordando che la variazione di entropia è data da:[10]
- ,
allora la variazione si entropia nel passaggio dallo stato iniziale allo stato finale è data da:[11]
- .
Integrando si ottiene:
- .
Utilizzando l'equazione di stato dei gas perfetti e la relazione di Mayer, ed operando le opportune sostituzioni, è possibile riscrivere la relazione appena trovata anche in termini di pressione e di calore specifico a pressione costante:
- .
Si ricordi che in questi calcoli il calore specifico è stato assunto come costante della temperatura.
Entalpia[modifica | modifica wikitesto]
Per il gas ideale anche l'entalpia è funzione solamente della temperatura:
dove è la capacità termica a pressione costante.
Per un gas perfetto vale la relazione[senza fonte]:
- .
Note[modifica | modifica wikitesto]
- ^ Peter Atkins, Julio de Paula, Physical Chemistry, OUP Oxford, 2014, 1982, p. 33.
- ^ In alcuni casi, una distinzione è introdotta fra gas ideale e gas perfetto. Un gas perfetto è definito come un gas ideale che possieda un rateo dei calori specifici costante:
Si veda anche Philip A. Thompson, Compressible-Fluid Dynamics (PDF), 1988. - ^ (EN) Ideal gas, su goldbook.iupac.org.
- ^ (EN) Perfect gas, su britannica.com.
- ^ (EN) J. S. Rowlinson, James Joule, William Thomson and the concept of a perfect gas, in Notes Rec. R. Soc. 20, vol. 64, pp. 47-53.
- ^ (definibile dal fattore di comprimibilità z che misura lo scostamento del comportamento ideale da quello reale) in funzione dei parametri adimensionali : π = (Pressione della sostanza gassosa in questione / Pressione critica della sostanza gassosa in questione) < 0,15; φ = (Temperatura della sostanza gassosa in questione / Temperatura critica della sostanza gassosa in questione) > 1.
- ^ I gas perfetti, su sapere.it. URL consultato l'8 novembre 2014.
- ^ (EN) The Joule Expansion, su chem.arizona.edu. URL consultato l'8 novembre 2014 (archiviato dall'url originale il 13 giugno 2012).
- ^ (EN) Entropy, su grc.nasa.gov. URL consultato l'8 novembre 2014.
- ^ Paolo Mazzoldi, Massimo Nigro, Cesare Voci, Fisica - Volume I (seconda edizione), Napoli, EdiSES, 2010, ISBN 88-7959-137-1.p.456
- ^ Paolo Mazzoldi, Massimo Nigro, Cesare Voci, Fisica - Volume I (seconda edizione), Napoli, EdiSES, 2010, ISBN 88-7959-137-1.p.467
Bibliografia[modifica | modifica wikitesto]
- Philip A. Thompson, Compressible-Fluid Dynamics, Irving H. Shames, 1988.
- Paolo Mazzoldi, Massimo Nigro, Cesare Voci, Fisica - Volume I (seconda edizione), Napoli, EdiSES, 2010, ISBN 88-7959-137-1.