0,999...

In matematica, il numero decimale periodico 0,999…, anche scritto $0,{\bar {9}}$, $0,{\dot {9}}$ o $\ 0,(9)$, denota un numero reale uguale a 1.

In altre parole, le notazioni "0,999…" e "1" rappresentano il medesimo numero reale. L'uguaglianza è stata da tempo accettata dai matematici di professione e insegnata nei libri di testo. Sono state prodotte nel tempo numerose dimostrazioni di questa identità con vari sviluppi di numeri reali, diverse assunzioni e contesti storici e rivolte a diversi tipi di pubblico.

Negli ultimi decenni i ricercatori dell'insegnamento della matematica hanno studiato la recettività degli studenti verso questa uguaglianza. Molti la discutono o la rifiutano, almeno inizialmente . Molti vengono guidati dai libri di testo, dagli insegnanti e da ragionamenti aritmetici per accettare che i due numeri sono uguali. I ragionamenti degli studenti per negare o affermare l'uguaglianza sono solitamente basati su alcune intuizioni errate sui numeri reali; per esempio che ogni numero reale ha un'unica rappresentazione decimale, che gli infinitesimi diversi da zero esistono o che l'estensione di 0,999… ha un limite.

La non unicità di tale rappresentazione non è limitata al sistema decimale. Lo stesso fenomeno avviene in basi intere diverse da 10 e i matematici hanno quantificato i diversi modi di scrivere 1 in basi non intere. Questo fenomeno non è neppure ristretto al singolo numero 1: anche i numeri diversi da zero che hanno un numero limitato di cifre decimali hanno un gemello seguito da 9 periodico. Per semplificare, il decimale limitato è quasi sempre la rappresentazione preferita, il che contribuisce all'idea sbagliata che questa sia l'unica rappresentazione. Di fatto, una volta che si permettono le periodicità, tutti i sistemi numerici posizionali contengono un numero infinito di rappresentazioni alternative dei numeri. Per esempio 28,3287 è uguale a 28,3286999…, 28,3287000 o a molti altri. Queste diverse identità sono state usate per capire meglio gli schemi nelle rappresentazioni decimali delle frazioni e nella struttura di un semplice frattale, l'insieme di Cantor. Si usano anche per studiare il grado (cardinalità) di infinito dell'insieme dei numeri reali.

Possono essere costruiti sistemi numerici in cui non vi è più questa identità, ma solo fuori dai sistemi convenzionali di numerazione reale usati nella matematica elementare.

Introduzione

0,999… è un numero scritto nel sistema di numerazione decimale e una delle più semplici dimostrazioni che tale numero è uguale a uno si affida alle proprietà aritmetiche di questo sistema. Gran parte dell'aritmetica decimale — addizione, sottrazione, moltiplicazione, divisione e comparazione — usa manipolazioni al livello delle cifre che sono molto simili a quelle usate per gli interi. Come con gli interi, due decimali finiti con cifre diverse sono numeri diversi (si ignorano gli zeri periodici). In particolare, qualsiasi numero nella forma di 0,99…9, dove i 9 hanno una fine, è leggermente minore di 1.

Sbagliare a interpretare il significato dell'uso del "…" (Punti di sospensione) in 0,999… porta a non capire la sua uguaglianza a 1. L'uso dei punti in questo caso è diverso da quello fatto nel linguaggio o in 0,99…9, dove i punti specificano che una porzione finita non viene scritta, il che può solo essere interpretato come un numero utilizzando il concetto matematico di limite. Di conseguenza, nell'uso convenzionale della matematica, il valore assegnato alla notazione "0,999…" è il numero reale che è limite della successione (0,9; 0,99; 0,999; 0,9999; …).

Diversamente dal caso con gli interi e i decimali finiti, le altre notazioni possono anche rappresentare un singolo numero in diverse maniere. Per esempio usando le frazioni, ¹⁄₃ = ²⁄₆. I decimali infiniti, tuttavia, possono rappresentare lo stesso numero in due soli modi, uno dei quali deve terminare con una serie infinita di nove, mentre l'altro deve terminare (deve consistere di una serie di zeri periodici da un certo punto in avanti).

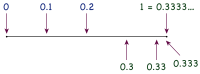
Ci sono molte dimostrazioni che 0,999… = 1, con vari livelli di coerenza matematica. Un breve abbozzo di una dimostrazione coerente può essere descritto semplicemente come segue: si consideri che due numeri reali siano identici se e solo se la loro differenza è uguale a zero. La maggior parte delle persone sarebbe d'accordo nel dire che la differenza tra 0,999… e 1, se esiste, deve essere molto piccola. Considerando la convergenza della successione sopra descritta, possiamo mostrare che la dimensione di questa differenza deve essere più piccola di qualsiasi quantità positiva e si può dimostrare che il solo numero reale con questa proprietà è 0. Poiché la differenza è 0 ne consegue che i numeri 1 e 0,999… sono identici. Lo stesso principio spiega anche perché 0,333… = ¹⁄₃, 0.111… = ¹⁄₉ eccetera.

Scetticismi nell'insegnamento

Gli studenti di matematica spesso rifiutano l'uguaglianza tra 0,999… e 1, con motivazioni che vanno dal loro diverso aspetto a dubbi sul concetto di limite e dissensi sulla natura degli infinitesimi. Ci sono molti fattori comuni che contribuiscono alla confusione:

• Gli studenti sono spesso "mentalmente legati alla nozione che un numero può essere rappresentato in un modo e uno soltanto in decimale". Vedere due numeri decimali manifestatamente differenti che rappresentano lo stesso numero sembra un paradosso, amplificato dal vedere l'apparentemente ben conosciuto numero 1.
• Alcuni studenti interpretano "0,999…" (o notazioni simili) come una serie numerosa ma finita di 9, eventualmente con una lunghezza variabile e non specificata. Se accettassero una stringa infinita di nove, si aspetterebbero comunque un ultimo 9 "a infinito".
• L'intuito e gli insegnamenti ambigui portano gli studenti a pensare al limite di una successione come un tipo di processo infinito piuttosto che a un valore preciso, poiché una successione non ha bisogno di raggiungere il proprio limite. Nel caso in cui gli studenti accettano la differenza tra una successione di numeri e il suo limite, potrebbero leggere "0,999…" come significato della successione e non come suo limite.
• Alcuni studenti pensano che 0,999… abbia un valore fisso inferiore a 1 di un infinitesimo diverso da zero.
• Alcuni studenti credono che il valore di una serie convergente sia al massimo un'approssimazione e quindi $0.{\bar {9}}\approx 1$.

Queste idee sono sbagliate nel contesto dei numeri reali standard, anche se alcune potrebbero essere valide in altri sistemi di numerazione, che siano inventate per la loro utilità matematica generale o come modo istruttivo per avere dei controesempi per capire meglio 0,999….

Molte di queste idee sono state raccolte dal professor David Tall, che ha studiato le caratteristiche dell'insegnamento e della cognizione che portano ad alcune delle incomprensioni incontrate nei suoi studenti. Intervistando i propri studenti per capire perché gran parte di loro inizialmente rifiutava l'uguaglianza, egli scoprì che "gli studenti continuavano a concepire 0,999… come una sequenza di numeri che si avvicinavano sempre di più a 1 e non come un valore fisso, perché 'non ha spiegato quante cifre ci sono' o 'è il numero decimale più vicino inferiore a 1' ".

Delle dimostrazioni elementare, la moltiplicazione di 0.333… = ¹⁄₃ per 3 è apparentemente la migliore per convincere gli studenti riluttanti che 0,999… = 1. Però, quando messi a confronto con il loro conflitto tra la certezza della prima equazione e l'incertezza della seconda, alcuni studenti cominciano a non credere più nella correttezza della prima o semplicemente diventano frustrati. Inoltre i metodi più sofisticati non sono più efficaci: gli studenti che sono perfettamente in grado di applicare definizioni coerenti potrebbero ancora cadere in immagini intuitive quando sorpresi da un risultato in matematica avanzata, incluso lo 0,999…. Per esempio, una studente di analisi fu capace di provare che 0.333… = ¹⁄₃ usando una definizione di estremo superiore, ma insisté che 0,999…<1 basandosi sulla sua recente comprensione delle divisioni lunghe. Altri ancora sono stati capaci di dimostrare che ¹⁄₃ = 0.333…, ma, messi a confronto con la dimostrazione frazionaria, insistono nel dire che la "logica" soppianta i calcoli matematici.

Il matematico Josef Mazur racconta la storia di un suo brillante studente di calcolo che "sfidava quasi tutto quello che dicevo in classe ma non dubitava mai della sua calcolatrice" e che era arrivato a credere che nove cifre sono tutto quello che serve per fare matematica, incluso il calcolo della radice quadrata di 23. Lo studente rimase a disagio con una piccola discussione sul fatto che 9.99… = 10, chiamandola "processo selvaggio immaginario a crescita infinita".

Dimostrazioni

Algebra

Frazioni

Un motivo per cui i decimali infiniti sono un'estensione necessaria di quelli finiti è quello di rappresentare le frazioni. Usando la divisione, una semplice frazione di interi come ¹⁄₃ diventa un numero periodico, 0.333…, nel quale le cifre si ripetono all'infinito. Questo numero decimale porta a una rapida dimostrazione di 0.999… = 1. La moltiplicazione di 3 volte 3 produce 9 su ogni cifra, quindi 3 × 0.333… è uguale a 0.999…. E 3 × ¹⁄₃ è uguale a 1, quindi 0.999… = 1.

Un'altra forma di questa dimostrazione moltiplica ¹/₉ = 0.111… per 9.

${\begin{aligned}0.333\dots &{}={\frac {1}{3}}\\3\times 0.333\dots &{}=3\times {\frac {1}{3}}={\frac {3\times 1}{3}}\\0.999\dots &{}=1\end{aligned}}$

${\begin{aligned}0.111\dots &{}={\frac {1}{9}}\\9\times 0.111\dots &{}=9\times {\frac {1}{9}}={\frac {9\times 1}{9}}\\0.999\dots &{}=1\end{aligned}}$

Una versione ancora più semplice della stessa dimostrazione si basa sulle seguenti equazioni:

$1={\frac {9}{9}}=9\times {\frac {1}{9}}=9\times 0.111\dots =0.999\dots$

Siccome sono valide entrambe le frazioni, per la proprietà transitiva 0.999… deve essere uguale 1. Similmente ³/_{3 = 1 e ³/3 = 0.999…. Quindi 0.999… deve uguagliare 1.}

Manipolazione delle cifre

Un altro tipo di dimostrazione si adatta più facilmente ad altri decimali periodici. Quando un numero in notazione decimale viene moltiplicato per 10 le cifre non cambiano, ma viene spostato il separatore decimale di una posizione verso destra. Quindi 10 × 0.999… è uguale a 9.999…, che è maggiore di 9 rispetto al numero originale.

Per vedere questo, si consideri che la sottrazione di 0.999… da 9.999… può procedere cifra per cifra; in ogni cifra dopo il separatore decimale il risultato è 9 ‒ 9, cioè 0. Ma gli zeri periodici non cambiano un numero, quindi la differenza è esattamente 9. Il passo finale usa l'algebra. Sia chiamato il numero decimale in questione, 0.999…, c. Allora 10c − c = 9. Questo è lo stesso che dire 9c = 9. Dividere entrambi i membri per 9 completa la dimostrazione: c=1. Scritta come sequenza di equazioni:

${\begin{aligned}c&=0.999\ldots \\10c&=9.999\ldots \\10c-c&=9.999\ldots -0.999\ldots \\9c&=9\\c&=1\\0.999\ldots &=1\end{aligned}}$

La validità della manipolazione delle cifre nelle due dimostrazioni sopra non va presa per fede o per assioma; segue dalla relazione fondamentale tra i decimali e i numeri che essi rappresentano. Sicuramente questa relazione (che può essere sviluppata in diverse maniere equivalenti) stabilisce di gia che i decimali 0,999… and 1,000… rappresentano entrambi lo stesso numero.

Analisi reale

Siccome la questione di 0,999… non riguarda lo sviluppo formale della matematica, si può posporre fino a che qualcuno non dimostra i teoremi classici dell'analisi reale. Un requisito è caratterizzare i numeri reali che possono essere scritti in notazione decimale, che consistono in un segno (opzionale), una sequenza finita di un qualsiasi numero di cifre che formi la parte intera, un separatore decimale e una sequenza di cifre che forma la parte frazionaria. Nell'obiettivo di discutere 0,999…, la parte intera può essere riassunta come b₀ così da avere un'espansione decimale con la forma:

$b_{0}.b_{1}b_{2}b_{3}b_{4}b_{5}\dots$

È vitale che la parte frazionaria, diversamente da quella intera, non sia limitata a un numero finito di cifre. Questa è una notazione posizionale, quindi, per esempio, il 5 in 500 contribuisce dieci volte rispetto al 5 in 50 e il 5 in 0,05 contribuisce un decimo rispetto al 5 in 0,5.

Serie e successioni infinite

Forse lo sviluppo più comune delle espansioni decimali è definirle come somme di serie infinite. In generale:

$b_{0},b_{1}b_{2}b_{3}b_{4}\ldots =b_{0}+b_{1}({\tfrac {1}{10}})+b_{2}({\tfrac {1}{10}})^{2}+b_{3}({\tfrac {1}{10}})^{3}+b_{4}({\tfrac {1}{10}})^{4}+\cdots .$

Per 0,999… si può invece applicare il più potente teorema della convergenza sulle serie geometriche:

Se $|r|<1$ allora $ar+ar^{2}+ar^{3}+\cdots ={\frac {ar}{1-r}}.$

Siccome 0,999… è una somma tale da avere un rapporto comune di $r=\textstyle {\frac {1}{10}}$, il teorema ha bisogno di un breve lavoro per dimostrare la questione:

$0.999\ldots =9({\tfrac {1}{10}})+9({\tfrac {1}{10}})^{2}+9({\tfrac {1}{10}})^{3}+\cdots ={\frac {9({\tfrac {1}{10}})}{1-{\tfrac {1}{10}}}}=1.\,$

Questa dimostrazione (effettivamente che 10 uguaglia 9,999…) appare nel 1770 nel libro Elementi di Algebra (Elements of Algebra) di Eulero.

Limiti: l'intervallo unitario, inclusa la sequenza decimale in base-4 che converge a uno (.3, .33, .333, …).

La somma di una serie geometrica è lei stessa un risultato più vecchio di Eulero. Una derivata tipica del XVIII secolo usava una manipolazione termine a termine simile alla dimostrazione algebrica data sopra e nel 1811 il libro di Bonnycastle Un'introduzione all'Algebra (An Introduction to Algebra) usa un argomentazione simile per le serie geometriche per giustificare la stessa manovra su 0,999… Una reazione del XIX secolo contro tali metodi di somma liberali risultò nella definizione che ancora domina oggi: la somma di una serie è definita come il limite della successione delle sue somme parziali. Una dimostrazione corrispondente del teorema calcola esplicitamente quella successione; può essere trovata in una qualsiasi introduzione basata su dimostrazioni al Calcolo o all'Analisi.

Una successione (x₀, x₁, x₂, …) ha come limite x se la distanza |x − x_n| diviene arbitrariamente piccola con l'aumentare di n. L'affermazione 0.999… = 1 può essere interpretata e dimostrata come un limite:

$0.999\ldots =\lim _{n\to \infty }0.\underbrace {99\ldots 9} _{n}=\lim _{n\to \infty }\sum _{k=1}^{n}{\frac {9}{10^{k}}}=\lim _{n\to \infty }\left(1-{\frac {1}{10^{n}}}\right)=1-\lim _{n\to \infty }{\frac {1}{10^{n}}}=1.\,$

L'ultimo passo — che lim ¹/_10ⁿ = 0 — è spesso giustificato dall'assioma che i numeri reali hanno la proprietà archimedeana. Questo modo di pensare verso 0,999… basato sui limiti viene spesso espresso in termini più evocativi che precisi. Per esempio, il libro del 1846 Aritmetica universitaria (The University Arithmetic) spiega: "0,999 +, continuato all'infinito = 1, perché ogni aggiunta di un 9 porta il valore più vicino a 1"; il libro del 1895 Aritmetica per le scuole (Arithmetic for Schools) dice, "…quando un grande numero di 9 viene preso, la differenza tra 1 e 0,99999… diviene inconcepibilmente piccola". Tali euristiche sono spesso interpretate dagli studenti come implicanti del fatto che 0,999… è più piccolo di 1.

Intervalli annidati ed estremi superiori

Intervalli annidati: in base 3, 1 = 1.000… = 0.222…

La definizione di serie sopra è un semplice modo di definire il numero reale espresso da una periodicità decimale. Un approccio complementare è fatto su misura del processo inverso: per un dato numero reale si definisce/definiscono le espansioni decimali che gli danno il nome.

Se un numero reale x è risaputo incluso nell'intervallo chiuso [0, 10] (è maggiore o uguale a 0 e minore o uguale a 10), si può immaginare di dividere quell'intervallo in 10 parti che si sovrappongono solo nei loro limiti: [0, 1], [1, 2], [2, 3] fino a [9, 10]. Il numero x deve appartenere a uno di essi; se appartiene a [2, 3] si registra la cifra "2" e si suddivide l'intervallo in [2, 2,1], [2,1, 2,2] …, [2,8, 2,9], [2,9, 3]. Continuando questo processo si ottiene una successione infinita di intervalli annidati, classificata da una successione infinita di cifre b₀, b₁, b₂, b₃, …, e si può scrivere:

x = b₀,b₁b₂b₃…

In questo formalismo il fatto che 1 = 1,000… e 1 = 0,999… riflette il fatto che 1 giace in entrambi [0, 1] e [1, 2], così da permettere la scelta di entrambi i sottointervalli per trovare le sue cifre. Per assicurarsi che questa notazione non abusi del segno di "=", è necessario un modo di ricostruire un numero reale unico per ogni decimale. Questo può essere fatto attraverso i limiti, ma altre interpretazioni insistono sull'argomentazione dell'ordinamento.

Una scelta diretta è il teorema degli intervalli annidati, che garantisce, data una successione di intervalli annidati chiusi le cui lunghezze divengono arbitrariamente piccole, gli intervalli contengono esattamente un numero reale nella loro intersezione. Quindi b₀,b₁b₂b₃… è definito essere l'unico numero contenuto in tutti gli intervalli [b₀, b₀ + 1], [b₀.b₁, b₀.b₁ + 0.1], e così via. 0,999… è allora l'unico numero reale che giace in tutti gli intervalli [0, 1], [0,9, 1], [0,99, 1], and [0,99…9, 1] per ogni stringa finita di 9. Siccome 1 è elemento di ciascuno di questi intervalli, 0,999… = 1.

Il Teorema degli Intervalli Annidati viene solitamente trovato in una caratteristica più fondamentale dei numeri reali: l'esistenza di un estremo superiore. Per sfruttare direttamente questi oggetti, si potrebbe definire b₀,b₁b₂b₃… essere l'estremo superiore della serie di approssimazioni {b₀, b₀.b₁, b₀.b₁b₂, …}. Si può poi dimostrare che questa definizione (o definizione degli intervalli annidati) è consistente con la procedura di suddivisione, implicando ancora 0,999… = 1. Tom Apostol conclude:

Il fatto che un numero reale potrebbe avere due diverse rappresentazioni decimali è semplicemente un riflesso del fatto che due differenti gruppi di numeri reali possono avere lo stesso estremo superiore.

Numeri reali

Alcuni approcci definiscono esplicitamente i numeri reali per essere certamente strutture costruite sui numeri razionali, usando la teoria degli insiemi. I numeri naturali — 0, 1, 2, 3, e così via — cominciano con 0 e continuano a crescere, cosicché ogni numero ha un successore. Si possono estendere i numeri naturali con i loro negativi per ottenere tutti gli interi e per estendere ulteriormente i rapporti, dando i numeri razionali. Questi sistemi numerici sono accompagnati dall'aritmetica dell'addizione, della sottrazione, della moltiplicazione e della divisione. Più sottilmente, includono l'ordinamento, così da poter confrontare un numero con un altro ed essere minore, maggiore o uguale.

Il passo dai numeri razionali ai numeri reali è un'ulteriore estensione. Ci sono almeno due modi famosi per raggiungere questo scopo, entrambi pubblicati nel 1872: le sezioni di Dedekind e le Successioni di Cauchy. Le dimostrazioni che 0,999… = 1 che usino direttamente queste costruzioni non si trovano nei libri di testo di analisi reale, dove la tendenza moderna degli ultimi decenni è stata quella di usare un'analisi assiomatica. Anche quando viene offerta una costruzione, esso viene applicato solitamente per dimostrare gli assiomi dei numeri reali, i quali poi supportano le dimostrazioni sopracitate. Tuttavia diversi autori esprimono l'idea che cominciare con una costruzione è più appropriato logicamente e le dimostrazioni risultanti sono più auto-contenute.

Sezioni di Dedekind

Nell'approccio con le sezioni di Dedekind, ogni numero reale x viende definito come l'insieme infinito di tutti i numeri razionali minori di x. In particolare, il numero reale 1 è l'insieme di tutti i numeri razionali che sono minori di 1. Ogni rappresentazione decimale positiva determina facilmente una sezione di Dedekind: l'insieme dei numeri razionali minori di una qualche parte della rappresentazione. Quindi il numero reale 0.999… è l'insieme dei numeri razionali r tali che r < 0 o r < 0,9 o r < 0,99 o r minore di un qualche altro numero della forma ${\begin{aligned}1-({\tfrac {1}{10}})^{n}\end{aligned}}$. Ogni elemento di 0.999… è minore di 1, quindi è elemento del numero reale 1. Al contrario un elemento di uno è un numero razionale ${\begin{aligned}{\tfrac {a}{b}}<1\end{aligned}}$, il che implica ${\begin{aligned}{\tfrac {a}{b}}<1-({\tfrac {1}{10}})^{b}\end{aligned}}$. Siccome 0.999… e 1 contengono gli stessi numeri razionali, sono lo stesso insieme, quindi: 0.999… = 1.

La definizione di numeri reali come sezioni di Dedekind fu pubblicata da Richard Dedekind nel 1872. L'approccio sopra descritto per assegnare un numero reale a ogni rappresentazione decimale è causato da un articolo descrittivo intitolato "0.999… è uguale a 1?" ("Is 0.999 … = 1?") di Fred Richman nel Mathematics Magazine, che è mirato ai professori della matematica collegiale, specialmente al livello junior/senior e ai loro studenti. Richman nota che prendere le sezioni di Dedekind in un qualsiasi sottoinsieme denso dei numeri razionali porta agli stessi risultati; in particolare egli usa le frazioni decimali, per le quali la dimostrazione è più immediata: "Quindi vediamo che nella definizione tradizionale dei numeri reali, l'equazione 0.9* = 1 viene costruita dall'inizio". Una ulteriore modifica della procedura porta a una struttura differente che Richman è più interessato a descrivere; si vedano i Sistemi numerici alternativi più sotto.

Successioni di Cauchy

Un altro approccio per costruire i numeri reali usa l'ordinamento dei razionali meno direttamente. Prima, viene definita la distanza tra x e y come il valore assoluto |x − y|, dove il valore assoluto |z| viene definito come il massimo di z e −z, quindi mai negativo. Poi i reali vengono definiti come le successioni dei razionali che hanno le proprietà della successione di Cauchy usando questa distanza. Questo è, nella successione (x₀, x₁, x₂, …), una mappatura dai numeri naturali ai razionali; per ogni razionale positivo δ c'è un N tale che |x_m − x_n| ⁤ δ per ogni m, n > N. (La distanza tra i termini diviene più piccola di ogni razionale positivo).

Se (x_n) e (y_n) sono due successioni di Cauchy, allora si possono definire uguali come numeri reali se la successione (x_n − y_n) ha come limite 0. Il troncamento del numero decimale b₀,b₁b₂b₃… genera una successione di razionali di Cauchy; questa viene presa per definire il valore reale del numero. In questo formalismo quindi il compito è quello di mostrare che la successione di numeri razionali

$\left(1-0,\ 1-{9 \over 10},\ 1-{99 \over 100},\ \dots \right)=\left(1,\ {1 \over 10},\ {1 \over 100},\ \dots \right)$

ha come limite 0. Considerando il termine n-esimo della successione, per n=0,1,2,… si deve perciò dimostrare che

$\lim _{n\rightarrow \infty }{\frac {1}{10^{n}}}=0.$

Questo limite è ovvio; una possibile dimostrazione è che per ε = a/b > 0 si può prendere N = b nella definizione di limite di una successione. Quindi si ha ancora 0.999… = 1.

La definizione dei numeri reali come successioni di Cauchy fu pubblicata separatamente da Eduard Heine e Georg Cantor, entrambi nel 1872.

Generalizzazioni

Le dimostrazioni che 0,999… = 1 si possono generalizzare immediatamente in due modi. Primo, ogni numero diverso da zero con notazione decimale finita (equivalente agli infiniti zeri periodici) ha una controparte con 9 periodici. Per esempio 0,24999… eguaglia 0,25, esattamente come nel caso particolare considerato. Questi numeri sono esattamente le frazioni decimali, e sono fitti.

Secondo, un teorema paragonabile si applica su ogni radice o base. Per esempio in base 2 (il Sistema numerico binario) 0,111… è uguale a 1, mentre in base 3 (sistema numerico ternario) 0,222… è uguale a 1. I libri di testo di analisi reale solitamente saltano l'esempio di 0,999… e presentano una o entrambe queste generalizzazioni dall'inizio.

Esistono rappresentazioni alternative di 1 anche con basi non intere. Per esempio nella base aurea, le due rappresentazioni standard sono 1.000… e 0.101010… e vi sono infinite rappresentazioni che includono degli 1 adiacenti. Generalmente, per quasi tutti i q tra 1 e 2 c'è una quantità non numerabile di rappresentazioni di 1 in base q. D'altra parte vi è un insieme non numerabile di q (inclusi tutti i numeri naturali più grandi di 1) per i quali vi è soltanto una rappresentazione di 1 in base-q, oltre alla triviale 1,000…. Questo risultato fu ottenuto da Paul Erdős, Miklos Horváth e István Joó attorno al 1990. Nel 1998 Vilmos Komornik e Paola Loreti determinarono la più piccola di queste basi, la costante di Komornik-Loreti q = 1.787231650…. In questa base 1 = 0.11010011001011010010110011010011…; le cifre sono date dalla successione di Thue-Morse che non ha ripetizioni.

Una generalizzazione più estesa viene fatta con i sistemi numerici posizionali più generici. Anch'essi hanno rappresentazioni multiple e in un certo senso le difficoltà sono persino peggiori. Per esempio:

• Nel sistema ternario bilanciato, ¹/₂ = 0.111… = 1.111….
• Nel sistema fattoradico 1 = 1.000… = 0.1234….

Marko Petkovšek ha dimostrato che tali ambiguità sono conseguenze necessarie dell'uso di un sistema posizionale: per un qualsiasi sistema simile che definisce tutti i numeri reali, il set di reali con rappresentazioni multiple è sempre denso. Egli chiama la dimostrazione "un esercizio istruttivo nella topologia degli insiemi di punti elementare"; richiede il vedere gli insiemi di valori posizionali come spazi di Stone e notare che le loro rappresentazioni reali sono date da funzioni continue.

Bibliografia

• Alligood, Sauer, and Yorke, 4.1 Cantor Sets, in Chaos: An introduction to dynamical systems, Springer, 1996, ISBN 0-387-94677-2.

  This introductory textbook on dynamical systems is aimed at undergraduate and beginning graduate students. (p.ix)

• Tom M. Apostol, Mathematical analysis, 2e, Addison-Wesley, 1974, ISBN 0-201-00288-4.

  A transition from calculus to advanced analysis, Mathematical analysis is intended to be "honest, rigorous, up to date, and, at the same time, not too pedantic." (pref.) Apostol's development of the real numbers uses the least upper bound axiom and introduces infinite decimals two pages later. (pp.9–11)

• Bartle, R.G. and D.R. Sherbert, Introduction to real analysis, Wiley, 1982, ISBN 0-471-05944-7.

  This text aims to be "an accessible, reasonably paced textbook that deals with the fundamental concepts and techniques of real analysis." Its development of the real numbers relies on the supremum axiom. (pp.vii-viii)

• Richard Beals, Analysis, Cambridge UP, 2004, ISBN 0-521-60047-2.
• Berlekamp, E.R.; J.H. Conway; and R.K. Guy, Winning Ways for your Mathematical Plays, Academic Press, 1982, ISBN 0-12-091101-9.
• Martin Berz, Automatic differentiation as nonarchimedean analysis, Elsevier, 1992, pp. 439–450.
• Bryan H. Bunch, Mathematical fallacies and paradoxes, Van Nostrand Reinhold, 1982, ISBN 0-442-24905-5.

  This book presents an analysis of paradoxes and fallacies as a tool for exploring its central topic, "the rather tenuous relationship between mathematical reality and physical reality". It assumes first-year high-school algebra; further mathematics is developed in the book, including geometric series in Chapter 2. Although 0.999… is not one of the paradoxes to be fully treated, it is briefly mentioned during a development of Cantor's diagonal method. (pp.ix-xi, 119)

• Brian Burrell, Merriam-Webster's Guide to Everyday Math: A Home and Business Reference, Merriam-Webster, 1998, ISBN 0-87779-621-1.
• John B. Conway, Functions of one complex variable I, 2e, Springer-Verlag, 1978, ISBN 0-387-90328-3.

  This text assumes "a stiff course in basic calculus" as a prerequisite; its stated principles are to present complex analysis as "An Introduction to Mathematics" and to state the material clearly and precisely. (p.vii)

• Charles Davies, The University Arithmetic: Embracing the Science of Numbers, and Their Numerous Applications, A.S. Barnes, 1846.
• Frank C. DeSua, A system isomorphic to the reals, in The American Mathematical Monthly, vol. 67, November 1960, pp. 900–903.
• Dubinsky, Ed, Kirk Weller, Michael McDonald, and Anne Brown, Some historical issues and paradoxes regarding the concept of infinity: an APOS analysis: part 2, in Educational Studies in Mathematics, vol. 60, 2005, pp. 253–266, DOI: 10.1007/s10649-005-0473-0.
• Edwards, Barbara and Michael Ward, Surprises from mathematics education research: Student (mis)use of mathematical definitions (PDF), in The American Mathematical Monthly, vol. 111, May 2004, pp. 411–425.
• Herbert B. Enderton, Elements of set theory, Elsevier, 1977, ISBN 0-12-238440-7.

  An introductory undergraduate textbook in set theory that "presupposes no specific background". It is written to accommodate a course focusing on axiomatic set theory or on the construction of number systems; the axiomatic material is marked such that it may be de-emphasized. (pp.xi-xii)

• Leonhard Euler, Elements of Algebra, a cura di John Hewlett and Francis Horner, English translators., 3rd English edition, Orme Longman, 1822.
• Paul Fjelstad, The repeating integer paradox, in The College Mathematics Journal, vol. 26, January 1995, pp. 11–15, DOI: 10.2307/2687285.
• Anthony Gardiner, Understanding Infinity: The Mathematics of Infinite Processes, Dover, 2003, ISBN 0-486-42538-X.
• Timothy Gowers, Mathematics: A Very Short Introduction, Oxford UP, 2002, ISBN 0-19-285361-9.
• Ivor Grattan-Guinness, The development of the foundations of mathematical analysis from Euler to Riemann, MIT Press, 1970, ISBN 0-262-07034-0.
• H.B. Griffiths, P.J. Hilton, A Comprehensive Textbook of Classical Mathematics: A Contemporary Interpretation, London, Van Nostrand Reinhold, 1970, ISBN 0-442-02863-6. Template:LCC.

  This book grew out of a course for Birmingham-area grammar school mathematics teachers. The course was intended to convey a university-level perspective on school mathematics, and the book is aimed at students "who have reached roughly the level of completing one year of specialist mathematical study at a university". The real numbers are constructed in Chapter 24, "perhaps the most difficult chapter in the entire book", although the authors ascribe much of the difficulty to their use of ideal theory, which is not reproduced here. (pp.vii, xiv)

• A.J. Kempner, Anormal Systems of Numeration, in The American Mathematical Monthly, vol. 43, December 1936, pp. 610–617.
• Komornik, Vilmos; and Paola Loreti, Unique Developments in Non-Integer Bases, in The American Mathematical Monthly, vol. 105, 1998, pp. 636–639.
• W.G. Leavitt, A Theorem on Repeating Decimals, in The American Mathematical Monthly, vol. 74, 1967, pp. 669–673.
• W.G. Leavitt, Repeating Decimals, in The College Mathematics Journal, vol. 15, September 1984, pp. 299–308.
• Joseph Lewittes, Midy's Theorem for Periodic Decimals, in New York Number Theory Workshop on Combinatorial and Additive Number Theory, arXiv, 2006.
• A.H. Lightstone, Infinitesimals, in The American Mathematical Monthly, vol. 79, March 1972, pp. 242–251.
• Richard Mankiewicz, The story of mathematics, Cassell, 2000, ISBN 0-304-35473-2.

  Mankiewicz seeks to represent "the history of mathematics in an accessible style" by combining visual and qualitative aspects of mathematics, mathematicians' writings, and historical sketches. (p.8)

• Eli Maor, To infinity and beyond: a cultural history of the infinite, Birkhäuser, 1987, ISBN 3-7643-3325-1.

  A topical rather than chronological review of infinity, this book is "intended for the general reader" but "told from the point of view of a mathematician". On the dilemma of rigor versus readable language, Maor comments, "I hope I have succeeded in properly addressing this problem." (pp.x-xiii)

• Joseph Mazur, Euclid in the Rainforest: Discovering Universal Truths in Logic and Math, Pearson: Pi Press, 2005, ISBN 0-13-147994-6.
• James R. Munkres, Topology, 2e, Prentice-Hall, 2000, ISBN 0-13-181629-2.

  Intended as an introduction "at the senior or first-year graduate level" with no formal prerequisites: "I do not even assume the reader knows much set theory." (p.xi) Munkres' treatment of the reals is axiomatic; he claims of bare-hands constructions, "This way of approaching the subject takes a good deal of time and effort and is of greater logical than mathematical interest." (p.30)

• George Pedrick, A First Course in Analysis, Springer, 1994, ISBN 0-387-94108-8.
• Marko Petkovšek, Ambiguous Numbers are Dense, in American Mathematical Monthly, vol. 97, May 1990, pp. 408–411.
• Pinto, Márcia and David Tall, Following students' development in a traditional university analysis course (PDF), 2001, pp. v4: 57–64.
• Protter, M.H. and C.B. Morrey, A first course in real analysis, 2e, Springer, 1991, ISBN 0-387-97437-7.

  This book aims to "present a theoretical foundation of analysis that is suitable for students who have completed a standard course in calculus." (p.vii) At the end of Chapter 2, the authors assume as an axiom for the real numbers that bounded, nodecreasing sequences converge, later proving the nested intervals theorem and the least upper bound property. (pp.56–64) Decimal expansions appear in Appendix 3, "Expansions of real numbers in any base". (pp.503–507)

• Charles Chapman Pugh, Real mathematical analysis, Springer-Verlag, 2001, ISBN 0-387-95297-7.

  While assuming familiarity with the rational numbers, Pugh introduces Dedekind cuts as soon as possible, saying of the axiomatic treatment, "This is something of a fraud, considering that the entire structure of analysis is built on the real number system." (p.10) After proving the least upper bound property and some allied facts, cuts are not used in the rest of the book.

• Fred Richman, Is 0.999… = 1?, in Mathematics Magazine, vol. 72, n. 5, December 1999, pp. 396–400. Free HTML preprint: Fred Richman, Is 0.999… = 1?, su math.fau.edu, 8 giugno 1999. URL consultato il 23 agosto 2006. Note: the journal article contains material and wording not found in the preprint.
• Abraham Robinson, Non-standard analysis, Revised edition, Princeton University Press, 1996, ISBN 0-691-04490-2.
• Maxwell Rosenlicht, Introduction to Analysis, Dover, 1985, ISBN 0-486-65038-3.
• Walter Rudin, Principles of mathematical analysis, 3e, McGraw-Hill, 1976, ISBN 0-07-054235-X.

  A textbook for an advanced undergraduate course. "Experience has convinced me that it is pedagogically unsound (though logically correct) to start off with the construction of the real numbers from the rational ones. At the beginning, most students simply fail to appreciate the need for doing this. Accordingly, the real number system is introduced as an ordered field with the least-upper-bound property, and a few interesting applications of this property are quickly made. However, Dedekind's construction is not omitted. It is now in an Appendix to Chapter 1, where it may be studied and enjoyed whenever the time is ripe." (p.ix)

• Maurice Shrader-Frechette, Complementary Rational Numbers, in Mathematics Magazine, vol. 51, March 1978, pp. 90–98.
• Smith, Charles and Charles Harrington, Arithmetic for Schools, Macmillan, 1895.
• Houshang Sohrab, Basic Real Analysis, Birkhäuser, 2003, ISBN 0-8176-4211-0.
• Ian Stewart, The Foundations of Mathematics, Oxford UP, 1977, ISBN 0-19-853165-6.
• James Stewart, Calculus: Early transcendentals, 4e, Brooks/Cole, 1999, ISBN 0-534-36298-2.

  This book aims to "assist students in discovering calculus" and "to foster conceptual understanding". (p.v) It omits proofs of the foundations of calculus.

• D.O. Tall and R.L.E. Schwarzenberger, Conflicts in the Learning of Real Numbers and Limits (PDF), in Mathematics Teaching, vol. 82, 1978, pp. 44–49.
• David Tall, Conflicts and Catastrophes in the Learning of Mathematics (PDF), in Mathematical Education for Teaching, vol. 2, 1976/7, pp. 2–18.
• David Tall, Cognitive Development In Advanced Mathematics Using Technology (PDF), in Mathematics Education Research Journal, vol. 12, 2000, pp. 210–230.
• (German) Dr. Hans von Mangoldt, Reihenzahlen, in Einführung in die höhere Mathematik, 1st ed., Leipzig, Verlag von S. Hirzel, 1911.
• David Foster Wallace, Everything and more: a compact history of infinity, Norton, 2003, ISBN 0-393-00338-8.

Voci correlate

• Serie
• Infinito
• Numero decimale periodico
• Limite

Collegamenti esterni

• 0.999… = 1?
• Teorema di 0.999...
• Numeri periodici