Cubottaedro troncato
| Cubottaedro troncato | |||
|---|---|---|---|
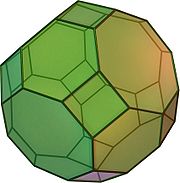 (Animazione) | |||
| Tipo | Solido archimedeo | ||
| Forma facce | Esagoni, ottagoni e quadrati | ||
| Nº facce | 26 | ||
| Nº spigoli | 72 | ||
| Nº vertici | 48 | ||
| Valenze vertici | 3 | ||
| Notazione di Wythoff | 2 3 4 | | ||
| Notazione di Schläfli | tr{4,3} o t0,1,2{4,3} | ||
| Diagramma di Coxeter-Dynkin |   
| ||
| Duale | Esacisottaedro | ||
| Proprietà | non chirale | ||
| Politopi correlati | |||
| |||
| Sviluppo piano | |||
 | |||
In geometria solida il cubottaedro troncato, detto pure grande rombicubottaedro, è uno dei tredici poliedri archimedei.
Occorre tenere presente che, nonostante il suo nome, il cubottaedro troncato (o tronco) non può essere ottenuto semplicemente troncando un cubottaedro con un rombododecaedro di opportune dimensioni. Infatti il rapporto tra le distanze dal baricentro delle facce di cubo e ottaedro è diverso per il cubottaedro (√3/2) e il cubottaedro tronco (3-√2)/√3 ; lo stesso accade per l'icosidodecaedro e l'icosidodecaedro tronco.
Area e volume[modifica | modifica wikitesto]
Indicando con a la lunghezza del lato, l'area A e il volume V sono:
Facce, spigoli, vertici[modifica | modifica wikitesto]
Il cubottaedro troncato ha 3 tipi differenti di facce: ci sono 12 quadrati, 8 esagoni regolari, 6 ottagoni regolari.
Come tutti i poliedri archimedei, il cubottaedro troncato è omogeneo nei vertici: per ogni coppia di vertici esiste una simmetria del solido che sposta il primo nel secondo. Come conseguenza, i 48 vertici hanno tutti la stessa valenza (3), e più generalmente la stessa cuspide.
Gli spigoli sono 72, tutti della stessa lunghezza.
Dualità[modifica | modifica wikitesto]
Il poliedro duale del cubottaedro troncato è l'esacisottaedro.
Altri solidi[modifica | modifica wikitesto]
Il cubottaedro troncato dà luogo ad altri solidi.
- I centri dei sei ottagoni sono vertici di un ottaedro regolare.
- I centri degli otto esagoni sono vertici di un cubo.
- I centri dei dodici quadrati sono vertici di un cubottaedro.
Bibliografia[modifica | modifica wikitesto]
- Henry Martin Cundy & A. P. Rollett, I modelli matematici, Milano, Feltrinelli, 1974.
- Maria Dedò, Forme, simmetria e topologia, Bologna, Decibel & Zanichelli, 1999, ISBN 88-08-09615-7.
- http://www.mi.sanu.ac.rs/vismath/zefirosept2011/_truncation_Archimedean_polyhedra.htm
Altri progetti[modifica | modifica wikitesto]
Wikimedia Commons contiene immagini o altri file sul cubottaedro troncato
Collegamenti esterni[modifica | modifica wikitesto]
- Cubottaedro troncato, in Enciclopedia della Matematica, Istituto dell'Enciclopedia Italiana, 2013.
- (EN) Eric W. Weisstein, Great Rhombicuboctahedron, su MathWorld, Wolfram Research.
