Utente:M&M987/Sandbox

Il titolo di questa pagina non è corretto per via delle caratteristiche del software MediaWiki. Il titolo corretto è Sistema di riferimento.

Si definisce in fisica sistema di riferimento l'insieme delle coordinate che individuano la posizione di un oggetto nello spazio. Spesso al concetto di sistema di riferimento è legato a quello di osservatore e si usa dire "sistema di riferimento dell'osservatore" oppure "del laboratorio" per definire un riferimento (di solito inerziale, ma non sempre) attraverso il quale studiare il sistema fisico. La trattazione matematica dei sistemi di riferimento ricade nel settore della geometria differenziale.

Excursus dei SDR in fisica

Un fondamentale postulato della meccanica classica, spesso reso più o meno implicito, afferma che lo spazio è tridimensionale, euclideo e isotropo. Osserviamo in dettaglio il postulato:

• Così come le dimensioni di un oggetto (es. un tavolo) sono identificate da tre numeri (tipicamente altezza, larghezza e profondità), in meccanica classica la posizione di un oggetto è tipicamente identificata da tre coordinate indipendenti, perciò l'oggetto vive in uno spazio tridimensionale;
• In spazio euclideo è definita una distanza euclidea: per esempio nel sistema di assi cartesiani (x,y,z) la distanza tra due punti è data dal teorema di Pitagora:

$d(P_{1},P_{2})={\sqrt {(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}+(z_{1}-z_{2})^{2}}}$

• L'isotropia dello spazio significa essenzialmente che le leggi fisiche sono le stesse in ogni punto dello spazio.

Per identificare le posizioni di n punti in uno spazio tridimensionale servono tre coordinate per punto, e quindi il totale è 3n. Come verrà spiegato meglio più avanti, in presenza di vincoli queste 3n coordinate non sono indipendenti e quindi è possibile adottare un sistema di riferimento che elimini le coordinate superflue.

In meccanica classica è spesso necessario introdurre sistemi di riferimento dipendenti dal tempo, per esempio per studiare un sistema fisico dal punto di vista di un osservatore in movimento. In quel caso le leggi di trasformazione da un sistema di riferimento all'altro dipenderanno dal parametro temporale e a seconda del tipo di trasformazione, potranno comparire forze fittizie dovute al fatto che la dinamica Newtoniana è invariante solo sotto cambi di coordinate che trasformino sistemi di riferimento inerziali in altri dello stesso tipo.

Il sistema di coordinate più naturali che descriva tutto lo spazio tridimensionale è quello cartesiano, ma sono possibili altri sistemi di riferimento quali quello cilindrico e quello sferico. A volte sistemi fisici semplici (per esempio il più semplice, un punto materiale) non si muovono in tutto lo spazio ma sono vincolati a muoversi su una curva o su una superificie. In quel caso è possibile introdurre un numero minore di coordinate indipendenti che descivano completamente la posizione del punto sul vincolo considerato.

In meccanica analitica per identificare completamente la posizione sistema si usano coordinate, dette coordinate generalizzate o lagrangiane, le cui caratteristiche fondamentali sono la reciproca indipendenza e l'eliminare i vincoli dalla trattazione del problema: si fa quindi un uso esteso di ascisse curvilinee così come di angoli nella identificazione delle posizioni di corpi rigidi in un sistema meccanico. Per esempio, dovendo studiare il moto di una sbarretta rigida nello spazio (la distanza, fissa, tra i due estremi della sbarretta costituisce infatti un vincolo) posso usare 6 coordinate cartesiane (3 per ogni estremo della sbarretta) oppure 5 coordinate generalizzate (3 per identificare il centro di massa della sbarretta e 2 angoli che indichino la sua orientazione nello spazio). Nello studio della dinamica del sistema alle coordinate generalizzate vengono affiancati i momenti canonici e l'insieme di coordinate lagrangiane e momenti canonici identifica pienamente l'evoluzione del sistema: in ogni istante il sistema verrà identificato da un punto nello spazio delle fasi che costituisce una varietà di dimensioni pari al doppio del numero di coordinate lagrangiane.

Sistema di riferimento in geometria differenziale

Dal punto di vista matematico adottare un sistema di riferimento significa identificare un punto appartenente ad una varietà differenziabile n-dimensionale tramite un diffeomorfismo, cioè una legge biunivoca differenziabile, su uno spazio euclideo di pari dimensioni: lo studio dei vari sistemi di riferimento appartinene quindi alla geometria differenziale. Una cosa da sottolineare è che cambiare il sistema di riferimento lascia invariata la struttura della varietà di partenza e quindi proprietà quali la distanza tra due punti, codificata nella metrica e la curvatura intrinseca della varietà, codificata dal tensore di Riemann, mentre cambia il modo con cui queste proprietà (per i tensori, le componenti dei tensori) si esprimono in un dato sistema di coordinate: questo fatto è molto importante ad esempio nella teoria della relatività generale, perché sono proprio gli invarianti che caratterizzano il campo gravitazionale prodotto dalla presenza o meno di masse nello spazio.

Meccanica classica

In meccanica classica gli eventi si svolgono in una varietà tridimensionale euclidea piatta, descritto nelle coordinate cartesiane dalla seguente metrica:

${\mbox{d}}s^{2}={\mbox{d}}x^{2}+{\mbox{d}}y^{2}+{\mbox{d}}z^{2}\,\!$

Cambiando sistema di riferimento, l'espressione della metrica cambierà (anche in modo molto complicato) ma non il suo valore numerico: essa è un invariante sotto cambi di coordinate.

Relatività ristretta

Nella teoria della relatività ristretta la varietà che si considera ingloba anche il tempo ed è perciò quadridimensionale: essa prende il nome di spazio-tempo. La curvatura della varietà è ovunque nulla, ma la metrica non è definita positiva, come si può vedere in un sistema di riferimento cartesiano:

${\mbox{d}}s^{2}=-{\mbox{d}}(ct)^{2}+{\mbox{d}}x^{2}+{\mbox{d}}y^{2}+{\mbox{d}}z^{2}=-{\mbox{d}}{x^{0}}^{2}+{\mbox{d}}{x^{1}}^{2}+{\mbox{d}}{x^{2}}^{2}+{\mbox{d}}{x^{3}}^{2}$

dove $\left\{x^{\mu }\right\}=(ct,x,y,z)=(x^{0},x^{1},x^{2},x^{3})$ sono le coordinate cartesiane. Uno spazio-tempo con questa metrica è chiamato spazio-tempo di Minkowski.

Relatività generale

Nella teoria della relatività generale la varietà che si considera (lo spazio-tempo di Minkowski) è quadridimensionale e curva: l'importanza della curvatura della varietà è data dal fatto che la forza gravitazionale è interpretata come una sua espressione, curvatura che viene modificata dalla presenza di masse. In assenza di masse, lo spaziotempo si riduce sempre (per il principio di equivalenza) allo spazio-tempo di Minkowski, che è l'ambiente proprio della relatività ristretta. Un esempio di metrica nello spazio tempo curvo è quella indotta da una massa puntiforme, non rotante, priva di carica elettrica, in coordinate sferiche:

$ds^{2}=-\left(1-{\frac {2M}{r}}\right)dt^{2}+\left(1-{\frac {2M}{r}}\right)^{-1}dr^{2}+r^{2}d\theta ^{2}+r^{2}\sin ^{2}\theta d\phi ^{2}$

Lo spazio-tempo dotato di questa metrica è detto spazio-tempo di Schwarzschild, dal nome del suo scopritore. È facile vedere che se la massa tende a zero, lo spazio-tempo ritorna ad essere quello piatto di Minkowski.

Sistemi di coordinate fissi

• 
  Coordinate polari.
• 
  Coordinate cartesiane (in 3D).
• 
  Coordinate cilindriche.
• 
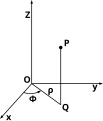
  Coordinate sferiche.

Coordinate cartesiane, coordinate polari, coordinate sferiche, coordinate cilindriche

Trasformazioni lineari e principio di relatività

Definendo un evento tramite la coordinata temporale e le tre coordinate spaziali (t, x, y, z), le trasformazioni lineari e affini si descrivono comodamente attraverso il formalismo matriciale, esprimendole tramite la matrice di trasformazione associata a quel cambio di coordinate. Una trasformazione è lineare quando le coordinate nel nuovo sistema di riferimento sono una combinazione lineare di quelle vecchie. Il ruolo del tempo in meccanica classica è del tutto particolare, in quanto la stragrande maggioranza delle volte è trattato nelle trasformazioni come un parametro. Si può pertanto scegliere di utilizzare matrici 4x4 che operino come l'identità sulla coordinata temporale oppure direttamente matrici 3x3, eventualmente dipendenti dal tempo, che operino sulle coordinate spaziali.

Trasformazioni indipendenti dal tempo

In fisica uno dei postulatiè il principio di relatività che afferma, in varie forme, l'invarianza delle leggi fisiche in diversi sistemi di coordinate. Spesso all'invarianza delle leggi segue una qualche grandezza conservata, come espresso dal teorema di Noether. La trasformazione identità è la trasformazione banale nella quale le nuove coordinate (indicate da un apice) sono uguali a quelle vecchie:

${\begin{matrix}{\text{Trasformazione identita}}'\\\left({\begin{matrix}t'\\x'\\y'\\z'\end{matrix}}\right)=\left({\begin{matrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{matrix}}\right)\left({\begin{matrix}t\\x\\y\\z\end{matrix}}\right)=\left({\begin{matrix}t\\x\\y\\z\end{matrix}}\right)\end{matrix}}$

Le trasformazioni di coordinate più semplici sono quelle indipendenti dal tempo come una traslazione o una rotazione. La traslazione si ottiene sommando un vettore (in questo caso costante) all'evento originario. Il significato fisico di una traslazione del sistema di riferimento è quello di cambiare il punto di osservazione, che è situato nell'origine del sistema di riferimento. Una traslazione si ottiene sommando un vettore alle vecchie coordinate: usualmente si considerano solo traslazioni spaziali (o semplicemente traslazioni), nelle quali si modificano solo le componenti spaziali dell'evento:

${\begin{matrix}{\text{Traslazione spaziale}}\\\left({\begin{matrix}t'\\x'\\y'\\z'\end{matrix}}\right)=\left({\begin{matrix}t\\x\\y\\z\end{matrix}}\right)+\left({\begin{matrix}0\\x_{0}\\y_{0}\\z_{0}\end{matrix}}\right)=\left({\begin{matrix}t\\x+x_{0}\\y+y_{0}\\z+z_{0}\end{matrix}}\right)\end{matrix}}$

La traslazione temporale è similmente definita dalla relazione $t'=t+t_{0}$. L'importanza della traslazione temporale è legata al conservazione dell'energia per i sistemi isolati: infatti se la lagrangiana di un sistema è invariante sotto traslazioni temporali, allora si conserva l'energia totale del sistema.

Una rotazione è invece una trasformazione che consiste nel definire un nuovo sistema di riferimento centrato nello stesso punto, ma con gli assi spaziali orientati diversamente; si può dimostrare che una trasformazione siffatta è data da una matrice ortogonale speciale. Come esempio, una rotazione lungo l'asse z di un angolo $\phi \,\!$ è data da:

${\begin{matrix}{\text{Rotazione (asse z)}}\\\left({\begin{matrix}t'\\x'\\y'\\z'\end{matrix}}\right)=\left({\begin{matrix}1&0&0&0\\0&\cos \phi &\sin \phi &0\\0&-\sin \phi &\cos \phi &0\\0&0&0&1\end{matrix}}\right)\left({\begin{matrix}t\\x\\y\\z\end{matrix}}\right)=\left({\begin{matrix}t\\\cos \phi x+\sin \phi y\\-\sin \phi x+\cos \phi y\\z\end{matrix}}\right)\end{matrix}}$

Trasformazioni galileiane

Le leggi meccanica classica sono invarianti sotto trasformazioni galileiane. Una generica trasformazione galileiana si ottiene combinando traslazioni e rotazioni indipendenti dal tempo con una o più traslazioni (spaziali) dipendenti linearmente dal tempo, chiamate boost di Galileo. Questo dipende dal fatto che nella legge di Newton compaiono solo le derivate seconde della posizione, e quindi eventuali termini lineari nel tempo non compaiono nell'accelerazione. Un boost di Galileo corrisponde a mettersi in un nuovo sistema di riferimento che si muove rispetto al primo di velocità ${\vec {v}}=(v_{x},v_{y},v_{z})$; la trasformazione prende la forma seguente:

${\begin{matrix}{\text{Boost di Galileo}}\\\left({\begin{matrix}t'\\x'\\y'\\z'\end{matrix}}\right)=\left({\begin{matrix}1&0&0&0\\-v_{x}&1&0&0\\-v_{y}&0&1&0\\-v_{z}&0&0&1\end{matrix}}\right)\left({\begin{matrix}t\\x\\y\\z\end{matrix}}\right)=\left({\begin{matrix}t\\x-v_{x}t\\y-v_{y}t\\z-v_{z}t\end{matrix}}\right)\end{matrix}}$

È da notare che per mezzo di queste trasformazioni la variabile temporale non viene in alcun modo modificata, ed è trattata alla stregua di un parametro: si possono considerare solo matrici 3x3 che operano sulle tre componenti spaziali, eliminando la prima riga e la prima colonna dalle matrici 4x4. Così facendo il boost di Galileo diventa semplicemente una somma tra vettori (di uno dipendente dal tempo):

$\left({\begin{matrix}x'\\y'\\z'\end{matrix}}\right)=\left({\begin{matrix}x\\y\\z\end{matrix}}\right)-\left({\begin{matrix}v_{x}t\\v_{y}t\\v_{z}t\end{matrix}}\right)=\left({\begin{matrix}x-v_{x}t\\y-v_{y}t\\z-v_{z}t\end{matrix}}\right)$

Forze apparenti

Qualunque trasformazione che non sia una combinazione di boosts di Galileo, traslazioni e/o rotazioni indipendenti dal tempo introduce dei termini aggiuntivi nell'equazione del moto, interpretabili come forze apparenti o, forse più appropriatamente, accelerazioni di trascinamento, come in questo esempio:

$\left({\begin{matrix}x'\\y'\\z'\end{matrix}}\right)=\left({\begin{matrix}\cos(\omega t)&\sin(\omega t)&0\\-\sin(\omega t)&\cos(\omega t)&0\\0&0&1\end{matrix}}\right)\left({\begin{matrix}x\\y\\z\end{matrix}}\right)=\mathbf {R} \left({\begin{matrix}x\\y\\z\end{matrix}}\right)$

La legge del moto nel sistema di riferimento vecchio (O) è ${\vec {F}}(t)=m{\vec {a}}=m{\vec {\ddot {x}}}(t)$

Nel nuovo sistema di riferimento la forza si trasforma semplicemente (${\vec {F}}'=\mathbf {R} {\vec {F}}$) ma l'accelerazione è invece pari a:

${\vec {a}}'={\frac {{\mbox{d}}^{2}(\mathbf {R} {\vec {x}})}{{\mbox{d}}t^{2}}}=\mathbf {R} {\vec {a}}+2{\dot {\mathbf {R} }}{\vec {v}}+{\ddot {\mathbf {R} }}{\vec {x}}={\vec {a}}'+2{\vec {\omega }}\wedge {\vec {v}}'-\omega ^{2}{\vec {x}}'\neq {\vec {a}}'$

Portando all'altro membro tutto ciò che non è l'accelerazione nel sistema di riferimento O' si ottiene infine:

${\vec {F}}'+m\omega ^{2}{\vec {x}}'-2m{\vec {\omega }}\wedge {\vec {v}}'={\vec {m}}a'$

${\vec {F}}'+{\vec {F}}_{app}=m{\vec {a}}'$

dove sono state evidenziate le forze apparenti.

Trasformazioni di Lorentz

Nella seconda metà del 1850 si è scoperto che le equazioni dell'elettromagnetismo cambiano forma sotto trasformazioni galileiane , il che rese incompatibili la meccanica classica e l'elettromagnetismo; Hendrik Antoon Lorentz calcolò che le trasformazioni che lasciavano invarianti le leggi dell'elettromagnetismo sono combinazioni di traslazioni, rotazioni e dei cosiddetti boosts di Lorentz. Un boost di Lorentz lungo una direzione data, per esempio lungo l'asse x, rappresenta come si trasformino le coordinate nel sistema di riferimento di un osservatore che si muove rispetto al primo di una velocità v rispetto l'asse x:

${\begin{matrix}{\text{Boost di Lorentz}}\\\left({\begin{matrix}ct'\\x'\\y'\\z'\end{matrix}}\right)=\left({\begin{matrix}\gamma &-\beta \gamma &0&0\\-\beta \gamma &\gamma &0&0\\0&0&1&0\\0&0&0&1\end{matrix}}\right)\left({\begin{matrix}ct\\x\\y\\z\end{matrix}}\right)=\left({\begin{matrix}\gamma (ct-\beta x)\\\gamma (x-\beta ct)\\y\\z\end{matrix}}\right)\end{matrix}}\quad {\text{con}}\quad \left\{{\begin{matrix}\beta ={\frac {v}{c}}\\\,\\\gamma ={\frac {1}{\sqrt {1-\beta ^{2}}}}\end{matrix}}\right.$

La cosa più importante da notare in questa trasformazione è il fatto che il tempo non è più considerato un parametro che non viene toccato dalle trasformazioni spaziali, ma diventa una coordinata di importanza pari alle altre: ciò significa che la visione classica di spazio e tempo distinti tra loro crolla e prende vita il concetto di spazio-tempo. La soluzione proposta da Albert Einstein nel 1905 al problema dell'incompatibilità tra meccanica ed elettromagnetismo fu modificare la meccanica classica proponendo nuove leggi del moto che risultassero invarianti rispetto alle trasformazioni di Lorentz, creando così una cinematica e una dinamica relativistiche.