Spaziotempo di Schwarzschild
Lo spaziotempo di Schwarzschild o metrica di Schwarzschild è una soluzione delle equazioni di campo di Einstein nel vuoto che descrive lo spaziotempo attorno a una massa a simmetria sferica, non rotante e priva di carica elettrica. È stata la prima soluzione esatta trovata per la relatività generale,[1] proposta da Karl Schwarzschild pochi mesi dopo la pubblicazione della teoria.[2]

Matematicamente, rappresenta la geometria di uno spazio-tempo statico e a simmetria sferica. Anzi, come dimostrato dal teorema di Birkhoff,[3] la staticità è una conseguenza della simmetria sferica e quella di Schwarzschild è la soluzione più generale che soddisfa queste due richieste.
Benché sia un'approssimazione (praticamente tutti i corpi celesti ruotano, Sole compreso), trova vaste applicazioni. I moti planetari attorno al Sole, ad esempio, che nella teoria della gravitazione newtoniana erano descritti[N 1] come moti in un campo di forze centrali, per cui erano valide le leggi di Keplero, sono descritti dalla relatività generale come moti di masse di prova (ossia moti geodetici) nello spazio-tempo di Schwarzschild. In particolare, se nella teoria kepleriana le orbite dei pianeti erano ellissi, in quella relativistica sono rosette (per approfondire si veda oltre) ed esibiscono una precessione dell'asse dell'orbita, che era stata osservata già tra il '700 e l '800 e non era spiegabile nel quadro newtoniano. In particolare i calcoli di Le Verrier, lo scopritore teorico, insieme con Adams, del pianeta Nettuno, sfruttando la teoria delle perturbazioni secolari, riuscivano a spiegare quasi tutta la precessione osservata, tranne un residuo di meno di 50 secondi d'arco per secolo per il pianeta Mercurio. Il calcolo esatto permesso dalla soluzione di Schwarzschild per l'angolo di precessione di Mercurio rafforzò la prima prima prova a sostegno della teoria della relatività costituita dal calcolo approssimato ad opera dello stesso Einstein.
La soluzione di Schwarzschild è anche all'origine di una delle idee della fisica che più fortemente hanno stimolato l'immaginario collettivo, prestandosi spesso a speculazioni fantascientifiche: il buco nero. Come sarà mostrato meglio in seguito, se il corpo sorgente del campo gravitazionale è abbastanza denso, la soluzione di Schwarzschild prevede che attorno alla sorgente, a una distanza nota come raggio di Schwarzschild, esista una superficie ideale, detta orizzonte degli eventi che divide lo spazio-tempo in due regioni non connesse causalmente,[N 2] e che funziona come una membrana unidirezionale: tutto può entrare ma niente può uscire.[N 3]
In particolare neppure la luce, una volta entrata nel volume racchiuso dall'orizzonte degli eventi, non potrà più allontanarsene, e continuerà inesorabilmente a orbitare, inanellando giri attorno alla massa centrale. Poiché la luce non riesce a sfuggire dall'oggetto, John Archibald Wheeler, in un'intervista del 1968, per farsi capire dal giornalista, si espresse con un paragone: se l'oggetto si trovasse a passare davanti allo sfondo pieno di stelle della nostra galassia, l'osservatore sulla Terra non potrebbe vedere l'astro, ma vedrebbe nella sua posizione un "buco nero" rispetto allo sfondo luminoso. Da allora venne adottato questo termine, mentre il termine preciso è singolarità gravitazionale.
Generalità[modifica | modifica wikitesto]
Se si introducono coordinate locali sferiche, e una coordinata temporale, la metrica si scrive[4] (si usa qui una metrica di segnatura (1,3), ossia (+---)):
ove con si indica la massa della sorgente, con la costante di gravitazione universale e con la velocità della luce. Si noti che per , si ritrova lo spaziotempo di Minkowski; per , invece, la metrica di Minkowski si ottiene asintoticamente per .
Si noti che per la sorgente si è unicamente imposto che sia una sfera simmetrica, ma non che sia statica: perciò, ci si può attendere una radiazione gravitazionale (piccola rispetto all'energia emessa in altre forme) anche dall'esplosione di una supernova, che (muovendosi ad alta velocità) è ancora assimilabile ad una sfera simmetrica. Il medesimo risultato si ottiene nell'elettromagnetismo, in cui il campo elettromagnetico intorno ad una distribuzione di cariche-sorgenti di forma sferica non dipende dalla distribuzione radiale delle cariche.[la soluzione di Schwarzschild è nel vuoto, quindi parlare in questo modo di "sorgenti" è scorretto]
La scelta delle coordinate sferiche appare la più naturale, viste le simmetrie del problema, ma le componenti della metrica risultano singolari per . Nel corso degli anni sono stati introdotti differenti sistemi di coordinate locali, per mettere in mostra determinate caratteristiche della geometria dello spazio-tempo.
La metrica espressa in coordinate sferiche è indipendente dalle coordinate e : questo comporta l'esistenza di due campi vettoriali, detti di Killing, che corrispondono ad altrettante simmetrie dello spazio-tempo e quantità conservate.
Per la precisione la -invarianza comporta un'invarianza per traslazioni temporali, garantendo la conservazione dell'energia; la -invarianza comporta invece l'invarianza per rotazioni rispetto all'asse , conservando il momento angolare rispetto a tale asse.
È possibile scrivere la metrica in forma matriciale:
Essa è singolare nei punti ove è singolare la matrice . Per la metrica di Schwarzschild ciò avviene quando
Nel primo caso la singolarità è eliminabile cambiando coordinate (passando ad esempio alle coordinate di Kruskal, si veda oltre). Il valore è noto come raggio di Schwarzschild (ovvero la distanza dal centro della stella a cui si forma l'orizzonte degli eventi). Il fatto che tale singolarità sia dovuta solo a una cattiva scelta delle coordinate è verificato facilmente sapendo ad esempio che gli invarianti di curvatura non sono ivi divergenti, notando che le geodetiche possono essere prolungate attraverso l'orizzonte degli eventi, oppure considerando che il determinante della matrice non è divergente nel punto specificato. Nel secondo caso, viceversa, si tratta di una singolarità non eliminabile e corrisponde a una curvatura infinita dello spazio-tempo (gli invarianti di curvatura sono ivi divergenti), spesso raffigurata come un imbuto nel tessuto spazio-temporale.
Soluzione[modifica | modifica wikitesto]
La soluzione dell'equazione di campo di Einstein nel vuoto per la metrica, nelle sue componenti , parte sfruttando le condizioni poste sul problema. Consideriamo di poter scegliere un sistema di coordinate in cui la coordinata corrisponda alla coordinata temporale , mentre le coordinate siano le coordinate spaziali cartesiane. A questo punto sfruttando la simmetria sferica del problema le coordinate spaziali soddisfano l'invarianza rotazionale:
Per mezzo della scelta di un sistema di coordinate sferico l'invarianza rotazionale permette di scrivere la metrica in linea generale come:
dove sono funzioni arbitrarie della sola coordinata radiale.
Il termine (equivalente a per la simmetria del tensore metrico) non è invariante sotto un'inversione temporale allora si può riscalare la coordinata temporale in modo da eliminare tale termine della metrica:
dove la funzione è arbitrariamente scelta per, come detto, eliminare il termine della metrica richiesto. Introducendo la funzione la metrica diventa:
Introduco anche per la coordinata radiale una riscalatura per mezzo del cambio di coordinate:
che permette di scrivere la metrica in forma diagonale:
Per semplicità di notazione chiamo le coordinate barrate senza la barra sopra e definisco una funzione incognita che racchiude il termine della metrica, allora:
La metrica trovata da considerazioni geometriche sul problema va risolta calcolando esplicitamente le funzioni incognite e ; ciò è fatto risolvendo l'equazione di campo di Einstein partendo dal calcolarsi i coefficienti della connessione di Levi-Civita (i simboli di Christoffel):
dove i termini riportati sono solo quelli non nulli.
Noti i coefficienti , calcolo i termini del tensore di Riemann per mezzo dei quali ottengo i termini del tensore di Ricci. Volendo risolvere l'equazione di campo nel vuoto allora i termini del tensore di Ricci vanno eguagliati a zero ottenendo così le quattro equazioni che ci permettono di poter determinare le funzioni incognite nella metrica:
Divido per l'equazione e analogamente per l'equazione e sommando le due equazioni ottenuto trovo la relazione:
A questo punto sfrutto l'ultima condizione sul problema, ossia che nel limite di distanze molto grandi dalla distribuzione delle sorgenti di massa la metrica tenda alla metrica di Minkowski. La condizione al bordo sulla metrica si esprime come che permette di trovare il valore della costante nella precedente relazione tra le funzioni:
Essendo, per quanto emerso, le due funzioni una l'inverso dell'altra è possibile esprimere i termini del tensore di Ricci nei soli contributi di una funzione (per esempio ), da cui allora sfruttando l'equazione ottengo:
Infine chiamo il valore della costante come che posso determinare nel limite di campo debole posto che il valore del termine della metrica sia:
quindi .
Lo spazio-tempo per sorgenti non troppo dense[modifica | modifica wikitesto]
Si è detto che la soluzione di Schwarzschild assume la sfericità e stazionarietà della massa sorgente. Tale situazione non è molto realistica, visto che praticamente tutti i corpi celesti ruotano, tuttavia lo spazio-tempo di Schwarzschild è un'ottima prima approssimazione (è possibile vedere[5] che il campo gravitazionale prodotto da qualunque sorgente si confonde con quello di Schwarzschild ponendosi abbastanza lontano dal corpo). Essa è adeguata per descrivere lo spazio-tempo attorno a corpi celesti non troppo densi, e permette di spiegare il comportamento di tutti i pianeti attorno al Sole, e dei satelliti attorno ai pianeti; ha consentito di stimare il corretto angolo di deflessione dei raggi luminosi attorno a un corpo celeste, e il ritardo temporale dei segnali che passano in prossimità del sole (effetto Shapiro[6][7][8]). La prima verifica sperimentale della bontà della teoria si ebbe con la corretta predizione dell'anomalia sull'angolo di precessione di Mercurio. A questo proposito è possibile con poca matematica derivare questo risultato fondamentale, come segue.
Come già detto, lo spazio-tempo di Schwarzschild possiede due campi vettoriali di Killing, a causa dell'indipendenza della metrica rispetto al tempo e all'angolo φ. Indichiamo tali vettori, in notazione di Cartan, come
È noto[9] che dato un campo di Killing , la quantità fisica conservata a esso associato è data da ove è la quadrivelocità lungo una geodetica, parametrizzata in modo affine da λ. Qui e nel seguito gli indici greci vanno da 0 a 3 e si usa la convenzione di Einstein sugli indici ripetuti;
Nel caso di Schwarzschild si hanno le due grandezze conservate:
e possono essere interpretate come l'energia e il momento angolare lungo la geodetica. Notiamo inoltre che, vista la simmetria dello spazio, una particella la cui orbita (cioè la proiezione spaziale della geodetica) si trovasse a un dato istante in un piano, continuera a muoversi nello stesso piano. Ciò equivale alla possibilità di considerare, per chiarezza e una volta per tutte, un moto sul piano equatoriale, fissando quindi
Possiamo dire qualcosa sull'evoluzione della coordinata radiale ricordando la relazione valida sempre per la quadrivelocità lungo una geodetica:
in cui la costante vale 1 per geodetiche di tipo tempo (particelle materiali), e zero per geodetiche di tipo luce (fotoni). Sviluppando questa equazione tenendo conto delle componenti della metrica di Schwarzschild, e delle quantità conservate, si ha:

che si può scrivere ordinando i termini:
Si noti che, seguendo l'approccio classico per cercare le traiettorie nello spazio-tempo, si sarebbe dovuto risolvere l'equazione della geodetica:
per arrivare alle stesso conclusioni, ma con un numero maggiore di calcoli.
Combinando le equazioni per e si ottiene l'equazione inversa per un'orbita chiusa
Sviluppando l'integrando in serie di supposto piccolo (il che è lecito per tutti i pianeti del sistema solare[N 4]), e con un po' di algebra è possibile calcolare la precessione su una rivoluzione come il doppio della precessione che si ha fra il perielio e l'afelio (vista la simmetria dell'orbita rispetto all'asse maggiore)[10]:
ove è il semilato retto dell'orbita (si veda ellisse). Inserendo i dati numerici si ottiene per il contributo alla precessione di Mercurio di origine puramente relativistica il valore:
L'ottimo accordo col valore sperimentale, misurato nuovamente negli anni quaranta, e pari a 43,11 secondi d'arco/secolo[11] contribuì a dare peso e credibilità alla teoria Einstaniana della gravitazione.
Lo spazio tempo per sorgenti estremamente dense - Buchi neri[modifica | modifica wikitesto]
La metrica di Schwarzschild presenta due singolarità, per e . La presenza della singolarità nell'origine delle coordinate non stupisce, in quanto la si ritrova anche nella teoria newtoniana della gravitazione. Più sorprendente è invece l'altra singolarità, visto che classicamente non se ne ha alcuna traccia; in particolare ci si può chiedere cosa avviene se la sorgente del campo è un corpo così denso, che la sua superficie è all'interno della sfera di raggio 2M, per cui tale distanza è accessibile a corpi esterni (massivi o meno).
Per dare un'idea, il raggio di Schwarzschild per il Sole è di poco meno di 3 km a fronte di un raggio "fisico" di quasi 700000 km, si intuisce dunque facilmente come siano richieste densità altissime perché il raggio fisico sia minore del raggio di Schwarzschild, e si abbia un buco nero.
È stato già anticipato che questa singolarità non è intrinseca dello spazio tempo, ma dovuta al particolare sistema di coordinate usato (singolarità coordinata).

Per capire meglio il comportamento dello spazio-tempo converrà quindi cambiare sistema di coordinate (operazione sempre consentita essendo le identità tensoriali soddisfatte in ogni sistema di riferimento)
Coordinate entranti di Eddington-Finkelstein[modifica | modifica wikitesto]
Si rivela pratico scegliere coordinate per cui le geodetiche radiali di tipo luce siano rappresentabili come rette inclinate di 45° in un diagramma spazio-tempo. Per il fotone si ha per cui l'equazione per le geodetiche radiali è:
ove abbiamo introdotto la coordinata radiale di Regge-Wheeler[12] :
usando questa coordinata radiale la metrica si scrive:
Introducendo infine la coordinata entrante nulla di Eddington-Finkelstein
Si noti che è inizialmente definita solo per ma può essere analiticamente estesa per tutti i valori di . Possiamo scrivere la metrica espressa nelle coordinate entranti di Eddington[13]-Finkelstein[14] :
A causa del termine misto, è immediato verificare come la metrica sia regolare per , per cui la singolarità di Schwarzschild è effettivamente di tipo coordinato.
Oltre a dimostrare la non singolarità fisica dell'orizzonte degli eventi, la metrica di Eddington-Finkelstein è molto adatta per capire come mai niente possa allontanarsi dal campo gravitazionale della sorgente una volta passato l'orizzonte degli eventi. Consideriamo per semplicità una geodetica radiale, per cui ; è possibile riarrangiare i termini della metrica in questo modo:
Trattiamo separatamente il caso di una particella massiva e di un fotone.
Per la particella massiva che si muove su una geodetica di tipo tempo, con la nostra convenzione sui segni, si ha ,inoltre per i punti all'interno dell'orizzonte degli eventi il coefficiente di è negativo. Riassumendo:
Il segno di non può essere arbitrario, poiché se consideriamo il moto "dal passato verso il futuro" si ha , in quanto v era stata definita come , per cui se il tempo aumenta anche il "tempo" deve aumentare. Per rendere negativo il prodotto si deve quindi avere
il che vuol dire che la distanza della particella dal centro dalla singolarità centrale può solo diminuire al trascorrere del tempo: la particella non può in nessun modo evitare la collisione con la massa centrale. Se si fosse considerato un fotone, al posto di una particella, l'unica differenza sostanziale sarebbe stato il porre , arrivando alle stesse conclusioni. Quindi neppure le onde elettromagnetiche possono allontanarsi dal campo gravitazionale della sorgente una volta che abbiano passato l'orizzonte degli eventi.
Questa caratteristica giustifica appieno il nome assegnato a questi corpi celesti: buchi neri, tale oggetto non permetterà infatti alla luce di lasciare il suo campo gravitazionale, e risulterà completamente invisibile a un osservatore esterno.
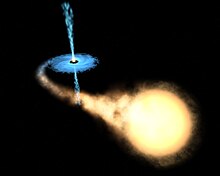
Per tale motivo un'osservazione diretta è impossibile, e le sole possibilità di rilevare la presenza di un buco nero, sono legate agli effetti che il suo campo gravitazionale intenso ha sui corpi celesti che eventualmente gli sono vicini. Si veda ad esempio l'immagine qui di lato che rappresenta il sistema stellare binario GRO J1655-40. Una delle componenti è supposta essere un buco nero: il suo campo gravitazionale è così intenso da sottrarre alla partner (in primo piano) la materia degli strati esterni, formando un caratteristico disco di accrescimento (disco blu in secondo piano).
Coordinate uscenti di Eddington-Finkelstein[modifica | modifica wikitesto]
Si noti come è possibile, partendo dalla metrica in coordinate sferiche, introdurre al posto della coordinata , vista prima, la coordinata uscente di Eddington-Finkelsteins , definita come:
anch'essa definita inizialmente all'esterno dell'orizzonte degli eventi, ma prolungabile in maniera analitica. Nelle coordinate la metrica si scrive:
Nella regione all'interno dell'orizzonte degli eventi, tale metrica descrive un comportamento esattamente opposto a quello visto prima. È facile infatti notare, seguendo lo stesso procedimento, che in questo caso la distanza di una particella (o fotone) dalla singolarità centrale, può solo aumentare col tempo.
A questa particolare soluzione viene dato il nome di soluzione di buco bianco. La presenza (a livello matematico) della soluzione di buco bianco era prevedile, essendo le equazioni di Einstein invarianti rispetto alla riflessione temporale; si deve tuttavia notare che a differenza della soluzione di buco nero, che vede la sua realizzazione fisica possibile a seguito del collasso stellare di una stella abbastanza massiva, senza particolari altre richieste, la formazione di un buco bianco prevede delle condizioni iniziali estremamente improbabili, ed è praticamente esclusa dalla congettura di Weyl, per cui essi non sono stati presi in considerazione seriamente dalla comunità scientifica, se non per un breve periodo,[N 5] rimanendo oggetto solo di speculazione fantascientifica.
Coordinate di Kruskal[modifica | modifica wikitesto]
È stato detto che le coordinate uscenti ed entranti di Eddington-Finkelstein descrivono comportamenti diversi all'interno dell'orizzonte degli eventi. È possibile introdurre un altro sistema di coordinate, quelle di Kruskal[15]-Szekeres[16], per avere una visione unitaria delle differenti possibili configurazioni per uno spazio-tempo di Schwarzschild. In queste coordinate la metrica si scrive (con segnatura +2 per ragioni di comodità):
ove le coordinate e sono definite al di fuori dell'orizzonte degli eventi, e sono legate alle coordinate entranti e uscenti dalle seguenti relazioni:
La vecchia coordinata radiale va intesa adesso come funzione di e , e definita implicitamente dalla relazione

La metrica di Kruskal è inizialmente definita per e , ma può essere estesa analiticamente per ogni valore delle due variabili; essa non presenta alcun comportamento particolare per .
In queste coordinate la singolarità centrale si ha per
per cui essa non sarà un punto, ma due archi di iperbole. L'orizzonte degli eventi è invece dato da:
cioè lungo gli assi .
Si noti che e sono coordinate radiali nulle, per cui i coni di luce avranno i lati lungo queste direzioni. Nell'immagine a lato è disegnato un tipico diagramma di Kruskal, gli assi e sono inclinati, in modo che nel grafico i coni di luce appaiano coi lati inclinati a 45°, e si considerano fissati i valori di e . Lo spazio tempo risulta in tal modo diviso in quattro regioni, corrispondenti ai quattro quadranti, e indicate nel disegno con numeri romani.
Le regioni corrispondenti alla soluzione di buco nero sono I (spazio-tempo fuori dall'orizzonte degli eventi) e II (interno dell'orizzonte), mentre le regioni III e IV corrispondono alla soluzione di buco bianco. È possibile vedere[N 6] come i moti a distanza costante dalla singolarità siano archi di iperbole nella regione I (rappresentati da punti dorati). La linea di punti blu rappresenta il moto di una particella materiale che oltrepassa l'orizzonte degli eventi e va a collidere con la singolarità centrale.
Con l'aiuto del grafico a lato, si vede facilmente del perché qualunque segnale fisico non possa, una volta superato l'orizzonte degli eventi, tornare nella regione I, o comunicare con essa. Considerando ad esempio il moto della massa (punti blu) ci si concentri nel punto P all'interno dell'orizzonte degli eventi, indicato in figura. Dal punto P essa potrà proseguire il suo moto solo in direzioni che sono all'interno del suo cono di luce futuro, andando quindi prima o poi a collidere contro l'arco di iperbole corrispondente a nella regione II. Se la massa fosse luminosa, essa potrebbe dal punto P, inviare segnali luminosi lungo i lati del suo cono: anch'essi finirebbero contro la singolarità centrale, e all'esterno dell'orizzonte degli eventi non si vedrebbe niente. Per quanto detto la regione I non può seguire causalmente la regione II.
Massima estensione analitica[modifica | modifica wikitesto]
Ricapitolando un po', si è visto come nella metrica di Schwarzschild, in coordinate sferiche, si incontrino "problemi" per . Le geodetiche (ad esempio radiali entranti) incontreranno l'orizzonte degli eventi per un valore finito del parametro affine (tempo proprio per particelle materiali). Tali geodetiche potranno essere prolungate, all'interno dell'orizzonte degli eventi, eventualmente con un opportuno cambio di coordinate (passando alle coordinate di Eddington-Finkelstein entranti, ad esempio), e andranno a interrompersi nella singolarità centrale (). È possibile definire come singolare uno spazio-tempo per cui esistono geodetiche che non possono essere prolungate per valori arbitrari del parametro affine, o, detto altrimenti, che si interrompono da qualche parte.
Procedendo in tal modo per tutte le geodetiche dello spazio, cambiando coordinate se necessario, è possibile dimostrare[5] che la metrica di Kruskal realizza la massima estensione analitica dello spazio-tempo di Schwarzschild, intendendo con ciò che tutte le geodetiche possono essere prolungate per valori arbitrari del parametro affine o terminano nella (provengono dalla, nel caso di buco bianco) singolarità centrale.
Soluzione interna[modifica | modifica wikitesto]

La soluzione di Schwarzschild si estende anche all'interno del corpo massiccio, che per ipotesi è sferico e di raggio dove vale l'equazione di Einstein "completa":
dove è il tensore di Einstein, e sono rispettivamente il tensore di Ricci e lo scalare di curvatura ottenuti a partire dal tensore di Riemann e è il tensore energia-impulso.
La metrica, date le ipotesi iniziali di stazionarietà e simmetria sferica è del tipo[N 7].:
dove e sono due funzioni della sola variabile .
È possibile riscrivere l'equazione di Einstein per ottenere la seguente equazione equivalente:
dove è la traccia di che si ottiene calcolando[N 8]:
Supponendo che l'interno della stella sia un fluido perfetto (che soddisfa l'equazione di Eulero), con densità e pressione si ha che il tensore energia-impulso è dato da:
dove sono vettori tali che .[N 9]
Si ricava che e quindi si ottengono le seguenti equazioni in componenti :
si può calcolare la somma , in modo da eliminare la pressione al secondo membro, ottenendo:
da cui si ricava:
si può riscrivere il primo membro come:
Quindi integrando entrambi i membri rispetto a tra e si ha:
Il termine a secondo membro può essere chiamato:
da cui si ricava infine:
La funzione si deve raccordare con la soluzione di Schwarzschild nel vuoto (ovvero per ) quando , quindi:
dove è la massa della stella (che compare anche nella metrica di Schawrzschild nel vuoto).
Se integrata in un intervallo con non rappresenta la massa della porzione di stella considerata infatti la massa dovrebbe essere data dall'integrale:
dove indica l'elemento di volume 3-dimensionale, la restrizione a tre dimensioni del determinante della metrica, per cui vale la relazione . Nell'ultimo passaggio il fattore deriva dall'integrale sulla parte angolare.
Dato che il fattore nell'ultimo integrale vale si ricava che , inoltre dato che abbiamo che . Infine chiamiamo:
dove è la massa propria e, per la diseguaglianza mostrata prima vale .
Per ottenere la funzione possiamo sfruttare la legge di conservazione su espressa come e ricordando la forma di si ha:
Si arriva infine a ottenere l'equazione
che per le componenti diventa , indicando che la pressione non dipende da e per la componente diventa
Note[modifica | modifica wikitesto]
- Annotazioni
- ^ In prima approssimazione, trascurando l'attrazione fra pianeti.[senza fonte]
- ^ In breve ciò vuol dire che gli osservatori di una regione non possono in alcun modo vedere quello avviene nell'altra. Si veda la bibliografia, con particolare riferimento a S.W. Hawking.[senza fonte]
- ^ Se si tiene conto di effetti quantistici, questa affermazione non è del tutto vera, si veda radiazione di Hawking.[senza fonte]
- ^ Per Mercurio tale numero vale circa 3 × 10−8, per gli altri pianeti è ancora più piccolo. Si veda ad es. H.C. Ohanian, in bibliografia
- ^ È possibile vedere sui siti delle più prestigiose riviste di fisica, come il Physical Review, che gli articoli sui buchi bianchi sono molto pochi, e si concentrano negli anni novanta.
- ^ Per approfondire si vedano ad es. S. Bergia e F. Alessandro, o R. D'Inverno, in bibliografia.
- ^ In questa sezione si usa la segnatura (-, +, +, +) per la metrica.
- ^ Nel seguito si farà uso della convenzione di Einstein nella particolare versione della notazione astratta degli indici, quindi indici ripetuti in posizione covariante e controvariante si intendono sommati.
- ^ Data la segnatura utilizzata i vettori di tipo tempo (o time-like) hanno norma negativa.
- Fonti
- ^ Karl Schwarzschild, On the gravitational field of a sphere of incompressible fluid according to Einstein's theory, Sitzungsber. Preuss. Akad. Wiss. Berlin (Math. Phys.) 1916 (1916), pagg. 424-434.
- ^ Albert Einstein, Zur allgemeinen Relativitatstheorie, Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften (1915) 778, Addendum-ibid. (1915) 799.
- ^ George David Birkhoff, Relativity and Modern Physics, Cambrigdge 1923, MA: Harvard University Press. LCCN 23008297
- ^ A. Urso, Considerazioni sul campo gravitazionale statico a simmetria centrale. (PDF) [collegamento interrotto], su sites.google.com.
- ^ a b si veda C.W. Mistern, K.S. Torn, J.A. Wheeler, in bibliografia
- ^ I.I. Shapiro, Phys.Rev.Let. 13 789 (1964)
- ^ I.I. Shapiro, G.H. Pettengill, M.E. Ash, M.L. Stone, W.B. Smith, R.P. Ingalls e R.A. Brockelman, Phys.Rev.Let. 20 1265 (1968)
- ^ I.I. Shapiro, G.H. Pettengill, M.E. Ash,D.B Campbell, R.B. Dyce, W.B. Smith, R.P. Ingalls e R.F. Jurgens, Phys.Rev.Let. 26 1132 (1971)
- ^ Si veda ad es. https://arxiv.org/PS_cache/gr-qc/pdf/9707/9707012v1.pdf
- ^ Per questo calcolo si veda ad es. S. Weinberg, in bibliografia
- ^ G.M. Clemence, Astron. Papers Am. Ephemeris, 11, part 1 (1943); Rev. Mod. Phys., 19, 361 (1947)
- ^ T.Regge, J.A. Wheeler, "Stability of a Schwarzschild singularity", Phys. Rev. 108, 1063 (1957)
- ^ A.S.Eddington, The mathematical theory of relativity,Cambridge University Press (1922)
- ^ D. Finkelstein, "Past-future asymmetry of the gravitational field of a point particle", Phys. Rev 110, 965 (1958)
- ^ M.D. Kruskal, Phys. Rev. 119, 1743 - 1745 (1960)
- ^ G. Szekeres, Publ. Math. Debrecen 7, 285, 1960
Bibliografia[modifica | modifica wikitesto]
- Silvio Bergia e Alessandro P. Franco, Le strutture dello spazio-tempo, Clueb, 2001.
- Subrahmanyan Chandrasekhar, Mathematical Theory of Black Holes, Oxford University Press, 1983.
- Ray d'Inverno, Introducing Einstein's relativity, Oxford University Press, 2006.
- Stephen Hawking e George Ellis, The large scale structure of the space-time, Cambridge Monographs on Mathematical Physics, 1973.
- Charles Misner, Kip Thorne e John Archibald Wheeler, Gravitation, W.H. Freeman and Company, 1972.
- Hans C. Ohanian, Gravitation and space time, W.W. Norton and Company, 1976.
- Hans Stephani, Dietrich Kramer, Malcolm MacCallum, Cornelius Hoenselaers e Eduard Herlt, Exact solutions of Einstein's field equations, Cambridge University Press, 2002.
- (EN) Paul K. Townsend, Black Holes (PDF), su arxiv.org, Cambridge, University of Cambridge, 4 luglio 1997.
- Robert M. Wald, General Relativity, University of Chicago Press, 1984.
- Steven Weinberg, Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity, John Wiley and Sons, 1972.

































![{\displaystyle {\begin{aligned}{\bar {r}}^{2}&=r^{2}C(r)\\d{\bar {r}}^{2}&=C(r)[1+{\frac {rC'(r)}{2C(r)}}]dr^{2}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8bdbbf7cecda1ade505a3b8c4c53482d89155c4f)









































































































![{\displaystyle {\dfrac {d}{dr}}\left[r\left(1-{\dfrac {1}{A}}\right)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b3daaad61aa99a642b4e291729e31d06bd3196a)



![{\displaystyle 2\cdot \left[4\pi \int _{0}^{r}\rho ({\tilde {r}}){\tilde {r}}^{2}d{\tilde {r}}\right]=2m(r),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8523dd6ee28dfc349cd06c71e5117f068cf43d36)








![{\displaystyle =4\pi \int _{0}^{r}{\tilde {r}}^{2}\left[1-{\dfrac {2m({\tilde {r}})}{\tilde {r}}}\right]^{-{\frac {1}{2}}}\rho ({\tilde {r}})d{\tilde {r}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a25da7cb0b621a0976b039436b3cb06f9d6dc6b)




![{\displaystyle \left[1-{\dfrac {2m({\tilde {r}})}{\tilde {r}}}\right]^{-{\frac {1}{2}}}>1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d5f3afa80541e415ff31e686ba34a828e41b2db)



![{\displaystyle {\tilde {m}}(R_{stella})=4\pi \int _{0}^{R_{stella}}{\tilde {r}}^{2}\left[1-{\dfrac {2m({\tilde {r}})}{\tilde {r}}}\right]^{-{\frac {1}{2}}}d{\tilde {r}}=M_{p},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6e4caedfdee84ba3582fbbe92fc0a0adc621e5c)



![{\displaystyle \nabla _{\mu }T^{\mu \nu }=\nabla _{\mu }[(\rho +P)u^{\mu }u^{\nu }-\nabla _{\mu }(Pg^{\mu \nu })={\dfrac {1}{\sqrt {-g}}}\partial _{\mu }[(\rho +P)u^{\mu }u^{\nu }]+(\rho +P)\Gamma _{\sigma \mu }^{\nu }u^{\mu }u^{\sigma }-g^{\mu \nu }\partial _{\mu }P=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2278c54ecbcf5b76746db3d26c3f06eb62171378)





