Strato limite di quantità di moto
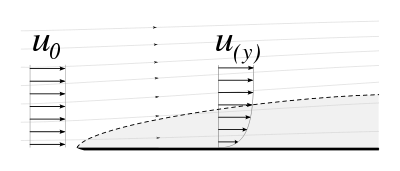
In fluidodinamica, lo strato limite, più precisamente detto strato limite di quantità di moto,[1] è una zona ideale di un flusso dove gli effetti causati dalla prossimità di una parete sono molto più marcati rispetto ad una zona esterna. Solitamente tale zona è individuata in uno strato di fluido nelle immediate vicinanze di una superficie solida.
Teoria dello strato limite[modifica | modifica wikitesto]
La teoria dello strato limite si basa sull'intuizione dell'aerodinamico tedesco Ludwig Prandtl, che dimostrò poi con evidenze sperimentali agli inizi del '900, la validità delle ipotesi fatte. Prandtl indicò come strato limite la zona al cui interno la velocità differisce per più dell'1% dalla velocità della porzione esterna di fluido, assumendo per l'esterno il modello di moto a potenziale. Prandtl ipotizzò inoltre che le dimensioni dello strato limite fossero piccole rispetto alle dimensioni del campo di moto esterno, assumendo che lo strato inizi in corrispondenza del bordo di ingresso della lastra. Di conseguenza, per le ipotesi fatte, le linee di corrente rimangono indisturbate fin tanto che non intersecano il bordo dello strato limite, iniziando da questo punto in poi a deflettere leggermente a causa del rallentamento della corrente.
Per correnti ad alti numeri di Reynolds è possibile confinare gli effetti della viscosità all'interno di una zona limitata adiacente alla parete; il flusso nella zona esterna si può considerare potenziale. Questo tipo di approssimazione semplifica notevolmente le equazioni di Navier-Stokes, permettendo di ottenere soluzioni approssimate. Si ricorda che le equazioni di Navier-Stokes sono equazioni alle derivate parziali che, allo stato attuale degli studi matematici, non sono risolubili per via analitica (se non in casi molto semplificati), ma in generale solo per via numerica.
Lo strato limite può essere di tipo laminare, dove i filetti fluidi sono appunto lamine che seguono il contorno del corpo, oppure turbolento, dove i filetti di fluido seguono linee intricate e non stazionarie. Lo strato limite può transitare da laminare a turbolento attraverso una zona detta regione di transizione, ma non potrà mai tornare spontaneamente laminare. La transizione dallo strato laminare a quello turbolento avviene in una zona di transizione che presenta caratteristiche di non stazionarietà. La transizione viene infine favorita dall'aumentare della velocità (o più correttamente dal numero di Reynolds) e dalla rugosità superficiale del corpo e dalla forma meno affusolata del corpo.
Trattazione dello strato limite[modifica | modifica wikitesto]
Come già accennato precedentemente la trattazione dello strato limite dipende in buona parte dalle condizioni iniziali a seconda della velocità della corrente che lambisce la parete interessata e di conseguenza dal rispettivo numero di Reynolds della corrente. Ciò nonostante si può pervenire ad una trattazione generale dello strato limite a prescindere dalla sua natura laminare o turbolenta applicando in entrambi casi le ipotesi che il moto sia di tipo:
- permanente;
- bidimensionale;
- trascurabile l'effetto della forza peso;
- unidirezionale.
Strato limite laminare[modifica | modifica wikitesto]
Nel caso dello strato limite laminare il problema può essere analizzato ricorrendo all'utilizzo delle equazioni di bilancio di massa per un volume di controllo e utilizzando successivamente il bilancio di quantità di moto. Applicando quindi il bilancio di massa,
dove con viene indicata la velocità del fluido che lambisce la parete, con una superficie orientata[2] e con δ lo spessore dello strato limite laminare. Esplicitando i singoli termini, indicando con y la direzione perpendicolare alla parete e con x la direzione parallela sia alla parete che alla corrente:
dove ql rappresenta il flusso di massa entrante dal bordo superiore. Dopo aver semplificato si ricava la seguente espressione:
A questo punto, si passa ad applicare il bilancio di quantità di moto:
per il termine a sinistra dell'equazione del bilancio di quantità di moto, che rappresenta la somma delle forze esterne agenti sul volume di controllo (volume di profondità unitaria), si ottiene
dove con τ si è indicato lo sforzo tangenziale sulla parete. Si noti inoltre che le pressioni agenti sulle facce si suppongano essere costanti, nonostante, in condizioni di corrente laminare, l'andamento delle pressioni ortogonalmente alle linee di corrente, per un fluido incomprimibile, sia di tipo idrostatico. Questa semplificazione nel caso di fluidi incomprimibili risulta comunque accettabile in virtù del fatto che lo strato limite si suppone essere di dimensioni molto ridotte. A questo punto semplificando e trascurando tutti gli infinitesimi di ordine superiore si ottiene infine
Per quanto riguarda invece il termine a destra nell'equazione del bilancio di quantità di moto si ottiene
Ricordando quindi l'espressione ricavata in precedenza per il termine ed inserendolo nell'equazione si ricava
Uguagliando i due termini ricavati si ottiene la seguente equazione
anche nota come equazione di von Kármán[3] che, nel caso di moto a potenziale nello strato esterno allo strato limite laminare, supponendo che
e
si semplifica nella seguente espressione
L'equazione può inoltre scriversi anche in forma adimensionale, raccogliendo alcuni termini nel seguente modo
ottenendo quindi l'equazione di von Kármán in forma adimensionale
A questo punto l'equazione può essere integrata facilmente non appena sia nota la distribuzione delle velocità. Per fare ciò è quindi necessario conoscere la distribuzione delle velocità. Nel caso di strato limite laminare il problema è stato risolto da Blasius nel 1908 secondo cui la soluzione è espandibile in serie di potenze. Tuttavia la soluzione di Blasius risulta laboriosa per cui sono state proposte diverse altre soluzioni. Tra quelle che approssimano meglio la distribuzione delle velocità va citata sicuramente la distribuzione di Pohlhausen[4] proposta nel 1921 che approssima la funzione con un polinomio di 4 grado del tipo
Teoria di Blasius[modifica | modifica wikitesto]
Per ricavare la distribuzione delle velocità secondo il modello di Blasius è necessario un approccio diverso da quello precedente. In un problema fluidodinamico la velocità del fluido immediatamente adiacente ad una superficie solida è considerata uguale alla velocità della parete stessa. A causa del fatto che la velocità varia con continuità dalla parete verso l'esterno e che il suo valore tende asintoticamente al valore esterno, lo spessore dello strato limite deve essere arbitrariamente definito, per convenzione, come lo strato di fluido all'interno del quale la velocità varia da zero fino al 99% (o 90%, o 95% a seconda della particolare convenzione che si preferisce adottare) della velocità della corrente fluida indisturbata (detta appunto velocità asintotica).
Infatti gli sforzi tangenziali diminuiscono con continuità allontanandosi dalla parete. Un osservatore invece percepisce una variazione marcata degli sforzi a causa del fatto che lo spessore dello strato limite è molto piccolo rispetto alle dimensioni del corpo.
Il modello base di questa teoria prende in considerazione l'equazione di stato dei gas perfetti:
dove p è la pressione, ρ la densità, R la costante specifica dei gas perfetti ed infine T la temperatura in kelvin.
E l'equazione di continuità della massa:
dove con il vettore V si è indicato il vettore velocità fluidodinamica, della quantità di moto:
e dell'energia:
Il sistema delle sei equazioni (tre scalari ed una vettoriale) viene semplificato con le seguenti ipotesi:
- il fluido è continuo (numero di Knudsen molto minore di 1), altrimenti non sono valide le equazioni precedenti;
- all'interno dello strato limite le variazioni lungo la coordinata parallela al flusso sono molto minori delle variazioni lungo la coordinata normale al flusso;
- flusso stazionario;
- flusso incomprimibile;
- flusso viscoso.
Infatti, indicando con δ lo spessore dello strato limite (funzione in generale di x, coordinata parallela alla parete ed al flusso) e con L una dimensione caratteristica del flusso (la lunghezza della parete o il diametro di un condotto, per esempio), si avrà certamente:
e perciò si può ipotizzare che le derivate rispetto ad x siano trascurabili rispetto a quelle rispetto ad y. Considerando fluidi incomprimibili (cioè a densità costante) e solo le direzioni x ed y (quindi un flusso bidimensionale) si semplifica dapprima l'equazione di continuità della massa, che per comodità scriviamo in forma vettoriale:[5]
ovvero, indicando con i pedici le derivate parziali:
Analogamente viene semplificata anche l'equazione di conservazione della quantità di moto, in forma vettoriale:
che diventa:
ed in forma estesa:
dove Dp rappresenta la diffusività cinematica.
Da queste equazioni si trascurano le derivate della componente verticale della velocità e la derivata seconda rispetto ad x della componente parallela al flusso della velocità. Ciò a causa del fatto che la velocità v è molto piccola rispetto ad u e le sue variazioni quindi sono minime. La mancanza del termine è dovuta al fatto che le variazioni lungo l'asse x siano notevolmente più piccole rispetto a quelle lungo l'asse y. Quest'ultima approssimazione fa in modo che la soluzione non risenta di tutto il dominio di integrazione, ovverosia ciò che succede a valle non perturba la soluzione a monte, semplificando notevolmente il calcolo. Il sistema delle equazioni di conservazione della massa e della quantità di moto diviene perciò:
Dette equazioni di Prandtl, anche se più propriamente solo la seconda equazione del sistema è l'equazione di Prandtl.
Accanto allo strato limite fluidodinamico, nel caso siano presenti fenomeni di trasmissione del calore nel fluido per via convettiva, può anche essere definito uno strato limite termico, come lo strato di fluido all'interno del quale la temperatura varia dal valore di parete fino al 99% (o altre percentuali a seconda della convenzione, valgono infatti le stesse considerazioni presentate per lo strato limite meccanico) del valore di temperatura esterno. L'ordine di grandezza del rapporto fra lo spessore dello strato limite fluidodinamico e quello dello strato limite termico è fornito dal numero di Prandtl.
Lo strato limite, di rilevante importanza nei problemi di aerodinamica ed in particolare nello studio delle superfici alari, è estendibile anche alla meteorologia ad allo studio delle correnti atmosferiche. È dovuto all'effetto della viscosità del fluido ed è collegato all'effetto Leidenfrost e, in particolare, al valore del numero di Reynolds (Re).
All'esterno dello strato limite il valore del numero di Reynolds è sufficientemente alto; in queste condizioni la regione esterna del flusso può essere considerata come ideale (viscosità trascurabile), che soddisfa cioè le equazioni di Eulero.
Nella regione vicino ai contorni solidi, invece questa approssimazione non può essere fatta perché bisogna rispettare le condizioni al contorno, che sono la condizione di aderenza (la velocità delle particelle di fluido a contatto con la parete deve essere nulla, in inglese è indicata come no slip condition) per lo strato limite della velocità, e la continuità del campo di temperatura sulla parete per lo strato limite termico.
Si considera quindi una lastra piana di apertura b e lunghezza . Partendo dalle equazioni di conservazione della massa e della quantità di moto, e considerando che nello strato limite , si ha
si introduce la variabile e la funzione di corrente , in modo che la soluzione trovata sarà simile per ogni x.
Si avrà
Derivando e sostituendo nelle equazioni di conservazione si ottiene
Le condizioni al contorno sono
Per un fluido newtoniano gli sforzi viscosi di taglio in prossimità della parete risultano uguali a
Si ha che
quindi
Integrando lungo la lastra (e considerando le due facce della lastra bagnata dal fluido) è possibile trovare il valore della resistenza d'attrito
o in termini adimensionali
Dove si è introdotto il numero di Reynolds locale:
inoltre il valore di è noto e pari a
Il coefficiente di forza medio sulla superficie della lastra risulta uguale a
Distribuzione delle velocità secondo Pohlhausen[modifica | modifica wikitesto]
Come accennato in precedenza l'approssimazione di Pohlhausen è data da un polinomio di quarto grado del tipo
Per potere quindi ricavare la distribuzione delle velocità all'interno dello strato limite sarà necessario disporre di cinque condizioni al contorno. Per lo strato adiacente alla parete, per le condizioni sono date da
mentre le condizioni al bordo esterno per η = 1 sono
La distribuzione di velocità che si ottiene nella seguente maniera è infine
Inserendo a questo punto la seguente espressione nell'equazione di von Karman è quindi possibile svolgere l'integrale dal quale si ottiene
Tuttavia l'espressione precedente contiene ancora due incognite e e necessita pertanto ancora di una seconda equazione per essere risolta. Questa è appunto fornita dal fatto che il fluido sia newtoniano. Si applica quindi l'equazione di Newton
Inserendo quindi il risultato così ottenuto nella relazione
ed integrando si ricava
dove la costante di integrazione può essere posta 0 in virtù del fatto che la velocità sul bordo inferiore adiacente alla parete è nullo. Rimanipolando l'espressione appena ricavata dividendo per x e facendo la radice quadra
si può quindi riscrivere l'espressione per lo sforzo tangenziale come
ossia
dove il termine
è anche noto come coefficiente di resistenza locale. Si noti che nel caso si fosse applicata la trattazione di Blasius il valore ricavato per il coefficiente di resistenza locale espresso come nel caso precedente sarebbe stato
A questo punto noto il coefficiente di resistenza locale e nota la geometria della parete è possibile calcolare la resistenza di una piastra immersa in un fluido.
Strato limite turbolento[modifica | modifica wikitesto]
Per valori del numero di Reynolds superiori a 3 · 105 lo strato limite inizia a divenire turbolento e la trattazione vista in precedenza non è più approssimata. Nel caso in cui il numero di Reynolds sia costante, il problema può comunque essere studiato nell'ipotesi di moto statisticamente stazionario, applicando la seguente scomposizione della velocità
ovvero scomponendo la velocità in un termine velocità media che si identifica con l'espressione e con un secondo termine che invece rappresenta la variazione media che si esprime come , nelle equazioni di Navier-Stokes, si ottengono le equazioni di Navier-Stokes mediate. Omettendo la sovralineatura sui termini velocità media e supponendo sempre che il moto sia di tipo bidimensionale, la prima equazione si scriverà dunque
Si possono adesso fare le seguenti ipotesi
e semplificare l'equazione, dove resta solo il seguente termine
Nel primo termine all'interno della parentesi tonda è immediato riconoscere lo sforzo viscoso mentre il secondo termine può essere interpretato come lo sforzo turbolento. Sempre dalla stessa equazione si evince che lo sforzo totale è la somma dei due sforzi e che questo si mantiene costante lungo l'asse verticale y. Mentre questa approssimazione si verifica sperimantalmente in prossimità della parete essa appare inaccettabile in prossimità del limite esterno dello strato limite, dove gli sforzi tendono asintoticamente a 0.
Lo strato limite viene quindi suddiviso in tre regioni che vengono studiate separatamente:
- regione interna
- buffer
- regione esterna.
Regione interna[modifica | modifica wikitesto]
La regione interna risulta essere la più importante sia per i bilanci delle forze che per i bilanci energetici. Inoltre in questa regione prevalgono gli sforzi viscosi, mentre quelli turbolenti possono essere trascurati. Lo sforzo agente risulta quindi essere
Dividendo entrambi i membri per ρ e ricordando che τ diviso ρ ha le dimensioni di una velocità al quadrato è possibile porre
dove u0 è una velocità fittizia. La relazione precedente si riscriverà quindi come
che si può esprimere come
dove è la viscosità cinematica. Infine, rendendo adimensionale la precedente equazione
ed esprimendo nelle nuove variabili adimensionali anche dette variabili interne,
la legge per lo strato interno si riassume come
Da osservazioni sperimentali si è osservato che tale legge è approssimata per valori di y+ < 5.
Buffer[modifica | modifica wikitesto]
Per valori di y+ compresi tra 5 e 30 l'effetto degli sforzi turbolenti non è più trascurabile e gli sforzi viscosi sono ugualmente importanti. Questa regione è chiamata buffer o semplicemente cuscinetto. Come nel caso della regione interna anche in questa regione ci sono teorie matematiche che permettono di ricavare la distribuzione delle velocità, tuttavia questa regione è caratterizzata da vortici intermittenti e da moti non stazionari, fatto che rende la trattazione relativamente complessa.
Pertanto nel corso degli anni sono state proposte diverse distribuzioni di velocità, molte delle quali dedotte sperimentalmente. Una delle distribuzioni utilizzate più di frequente è quella proposta da Spalding nel 1961 che normalmente viene scritta in forma implicita
dove il valore della costante B è fissato con 5,5, mentre per la costante di von Karman si utilizza il valore 0,4.
Regione esterna[modifica | modifica wikitesto]
Al contrario di quanto visto per la regione interna, nella regione esterna prevalgono gli sforzi di tipo turbolento. Essa si estende per valori della y+ compresi tra 35 e 50 ed è pertanto la regione più grande dello strato limite. Gli sforzi in questa regione possono essere indicati tramite la seguente espressione
Osservato quindi che in virtù del fatto che il moto è unidirezionale si osserva che il tensore degli sforzi è composto da un singolo termine. Pertanto appare lecito applicare all'equazione il modello diffusivo di Boussinesq riscrivendo il termine a destra dell'equazione precedente come segue
che sempre in virtù del fatto che il moto sia unidemensionale si riscrive semplicemente come
Inserendo quindi l'espressione ricavata nella prima equazione di partenza nella quale si erano trascurati il termine dello sforzo viscoso si ottiene
Si osservi inoltre che in assenza di componenti della velocità in direzione y si è trascurato il pedice della velocità x. A questo punto per integrare l'equazione è necessario introdurre un opportuno modello di chiusura. Si può quindi ad esempio utilizzare il modello di Prandtl secondo il quale si ha
con
l'equazione di partenza diviene
dove k indica la costante di von Karman il cui valore è compreso tra 0,4 e 0,41. Appurato che tutte le grandezze prese in esame sono positive e dopo aver estratto la radice quadrata positiva si ottiene
Rimanipolando l'equazione
e ricordando la definizione data in precedenza per y^+ e u^+ si ottiene
Integrando infine l'espressione precedente si giunge all'equazione che descrive l'andamento delle velocità nello strato esterno
Per calcolare la costante di integrazione B si dovrebbe conoscere il valore della velocità in una delle due estremità della regione esterna. Tuttavia nella maggior parte delle applicazioni non si conosce né la velocità del Buffer né quella del moto all'esterno dello strato limite e non è quindi possibile calcolare il valore della costante. Dal punto di vista applicativo però si potrebbe immaginare di trascurare il buffer ed immaginare di collegare la regione interna con quella esterna, supponendo che esista una transizione diretta dal sottostrato di turbolenza di parete al sottostrato viscoso. Le risultanze sperimentali di Nikuradse indicano che questo passaggio avviene per valori di y+ = 11,6, per cui questo valore è stato fissato con 5,5. Studi più recenti condotti nel 1986 effettuati da Coles e Hirst hanno invece corretto il valore calcolato da Nikuradse fissandolo a 5.
Approssimazione dello strato limite turbolento con un'unica legge di potenza[modifica | modifica wikitesto]
Per molte applicazioni, come il calcolo della resistenza, l'utilizzo delle tre distribuzioni di velocità può risultare poco agevole. In passato sono quindi state proposte diverse leggi, come approssimare con un'unica legge la distribuzione di velocità. Una tra le più note è la legge proposta da Schlichting nel 1968, che propone la seguente espressione
Si noti che anche questa legge è scritta in variabili interne. Inoltre la costante dell'esponente dovrebbe dipendere dal numero di Reynolds. Pertanto per la formula proposta da Schlichting sono stati consigliati dei correttivi. Hinze ad esempio propose per il valore dell'esponente di utilizzare il valore 8,3, mentre Clausre propose un valore compreso tra 0,3 e 0,1. Va inoltre precisato che la legge può essere anche estesa alla regione esterna.
Note[modifica | modifica wikitesto]
- ^ In quanto con l'accezione strato limite, nell'ambito dei fenomeni di trasporto, presenta un significato molto più ampio di quello sopra descritto.
- ^ Ovverosia un vettore avente modulo A, direzione normale (perpendicolare) ad A e verso uscente da A.
- ^ Dal nome del suo teorizzatore, l'ingegnere ungherese Theodore von Kármán.
- ^ Ernst Pohlhausen fu uno dei ricercatori che lavorarono con Prandtl.
- ^ Si ricorda che la derivata materiale temporale di una grandezza f è:
Voci correlate[modifica | modifica wikitesto]
Altri progetti[modifica | modifica wikitesto]
 Wikimedia Commons contiene immagini o altri file su strato limite di quantità di moto
Wikimedia Commons contiene immagini o altri file su strato limite di quantità di moto
Collegamenti esterni[modifica | modifica wikitesto]
- Strato limite: principali caratteristiche ed effetti (PDF), su diiar.polimi.it. URL consultato il 22 giugno 2009 (archiviato dall'url originale il 29 dicembre 2009).
| Controllo di autorità | J9U (EN, HE) 987007283990105171 · NDL (EN, JA) 00567209 |
|---|





















![{\displaystyle {\frac {\partial }{\partial t}}\left[\rho \left(e+{\frac {1}{2}}V^{2}\right)\right]+{\frac {\partial }{\partial x_{i}}}\left[\rho \left(e+{\frac {1}{2}}V^{2}\right)u_{i}\right]=\rho f_{i}u_{i}+{\frac {\partial \left(t_{ij}u_{i}\right)}{\partial x_{j}}}+{\frac {\partial }{\partial x_{i}}}\left(k{\frac {\partial T}{\partial x_{i}}}\right){.}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/11cbe3641b504347604c84903cdf91fda5984abc)













![{\displaystyle {\begin{array}{l}{\displaystyle u={\frac {\partial \Psi }{\partial y}}={\frac {\partial \Psi }{\partial \eta }}{\frac {\partial \eta }{\partial y}}={\sqrt {V_{\infty }x{\mathcal {D}}_{p}}}f'{\sqrt {\frac {V_{\infty }}{{\mathcal {D}}_{p}x}}}=V_{\infty }f'}\\{\displaystyle v=-{\frac {\partial \Psi }{\partial x}}=-\left[{\frac {1}{2}}{\sqrt {\frac {V_{\infty }{\mathcal {D}}_{p}}{x}}}f(\eta )-{\frac {1}{2}}{\sqrt {\frac {V_{\infty }{\mathcal {D}}_{p}}{x}}}f'\left(y{\sqrt {\frac {V_{\infty }}{{\mathcal {D}}_{p}x}}}\right)\right]={\frac {1}{2}}{\sqrt {\frac {V_{\infty }{\mathcal {D}}_{p}}{x}}}\left[\eta f'-f\right]}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85d00d198d0c9b588e2d76b7d85a6f1188d9d892)













































![{\displaystyle y^{+}=u^{+}+e^{-kB}\left[e^{(ku^{+})}-1-ku^{+}-{\frac {(ku^{+})^{2}}{2}}-{\frac {(ku^{+})^{3}}{6}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01de866bb7a7b6cbdfd52a17582188b9f0c8c67b)












