Scarto quadratico medio
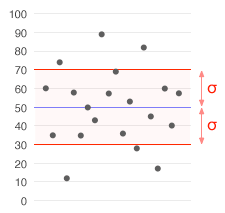
Lo scarto quadratico medio (o deviazione standard, o scarto tipo, o scostamento quadratico medio) è un indice di dispersione statistica, vale a dire un indicatore usato per fornire una stima sintetica della variabilità di una popolazione di dati o di una variabile casuale.
È uno dei modi per esprimere la dispersione dei dati intorno a un indice di posizione, quale può essere, ad esempio, la media aritmetica o una sua stima. Ha pertanto la stessa unità di misura dei valori osservati (al contrario della varianza che ha come unità di misura il quadrato dell'unità di misura dei valori di riferimento). In statistica, la precisione si può esprimere come lo scarto quadratico medio.
Il termine "standard deviation" è stato introdotto in statistica nel 1894 da Karl Pearson[1], assieme alla lettera greca (sigma) che lo rappresenta. Il termine italiano "deviazione standard" ne è la traduzione più usata nel linguaggio comune; il termine dell'Ente italiano di normazione è tuttavia "scarto tipo".[2]
Lo scarto quadratico medio è la radice quadrata della varianza[3], la quale viene coerentemente rappresentata con il quadrato di sigma, .
Statistica descrittiva
[modifica | modifica wikitesto]In statistica descrittiva lo scarto quadratico medio di un carattere rilevato su una popolazione di unità statistiche si definisce nel seguente modo:[4]
dove è la media aritmetica di . Ossia lo scarto quadratico medio è la radice quadrata della varianza.
A partire dallo scarto quadratico medio si definisce anche il coefficiente di variazione[5] o la deviazione standard relativa come il rapporto tra lo scarto tipo e il valore assoluto della media aritmetica della variabile in esame sempreché quella media sia non nulla:
Questo indice relativo (che viene spesso espresso in termini percentuali[6]) consente di effettuare confronti tra dispersioni di dati di tipo diverso, indipendentemente dalle loro quantità assolute.
Formulazioni equivalenti
[modifica | modifica wikitesto]Lo scarto quadratico medio può essere espresso in una forma equivalente, ricalcolando come segue la sommatoria dei quadrati degli scarti:
Applicando questo risultato alla formula originale per lo scarto quadratico medio, si ottiene:
Nelle applicazioni informatiche, è a volte conveniente modificare la formula precedente:
che consente, con sole tre variabili , di calcolare lo scarto quadratico medio, oltre che la media, di una successione di numeri di lunghezza senza dover ricorrere ad una memorizzazione degli stessi.
Statistica inferenziale
[modifica | modifica wikitesto]Nell'ambito della statistica inferenziale (dove è noto solo un campione, di numerosità , dell'intera popolazione), soprattutto nel contesto della teoria della stima, uno stimatore per lo scarto quadratico medio di un carattere è dato dallo scarto quadratico medio campionario:
dove è la media campionaria di (ossia la media aritmetica del carattere calcolata sul campione considerato).
Valgono i limiti e , dove indica la numerosità della popolazione di riferimento, quindi è un intero positivo oppure a seconda dei casi.
Poiché il precedente stimatore è distorto, per ottenerne uno non distorto si rimpiazza il denominatore con ottenendo:
Sostanzialmente, poiché non è nota la media dell'intera popolazione , ma solo una sua stima (la media del campione ), bisogna utilizzare per ottenere uno stimatore corretto della varianza incognita di sull'intera popolazione a partire dai dati del campione. La sua radice quadrata diviene lo scarto quadratico medio campionario "corretto".
Questa correzione al denominatore fa sì che sia maggiore rispetto a , correggendo così la tendenza di a sottostimare le incertezze, soprattutto nel caso in cui si lavori con pochi dati ( "piccolo"; nelle applicazioni pratiche, si considera "piccolo" un campione formato da meno di 30 elementi).
Osserviamo il caso limite di , cioè quando si ha un campione di un solo elemento. Si ha , che ovviamente non è molto ragionevole nell'ambito della statistica inferenziale. Invece non è definito, rispecchiando così la totale ignoranza inerente all'incertezza su una singola misura. In questo senso, si afferma che non dice nulla sul singolo caso.
La differenza tra e per campioni molto estesi diventa numericamente insignificante.
Probabilità
[modifica | modifica wikitesto]Sia una variabile aleatoria, lo scarto quadratico medio è definito come la radice quadrata della varianza di
Formalmente lo scarto quadratico medio di una variabile aleatoria può essere calcolato a partire dalla funzione generatrice dei momenti, in particolare è la radice quadrata della differenza tra il momento secondo ed il momento primo elevato al quadrato, cioè
dove è il valore atteso di .
Applicazioni
[modifica | modifica wikitesto]In fisica, lo scarto quadratico medio è un ottimo indice dell'errore casuale della misurazione di una grandezza fisica.
In ingegneria, è uno dei parametri da considerare per valutare la capacità di un processo produttivo, o più in generale, l'affidabilità di una campagna di test per determinare il tasso di guasto di un dato componente.
In ambito finanziario, viene usato per indicare la variabilità di un'attività finanziaria e dei suoi payoff (rendimenti). Esso fornisce quindi, implicitamente, una misura della volatilità dell'attività, quindi del suo rischio.
In ambito sportivo è utilizzato per valutare la prestazione di un giocatore di bowling in riferimento ad un certo numero di partite. Il valore trovato non incide sul punteggio ma sintetizza le capacità e i miglioramenti del giocatore.[7]
Note
[modifica | modifica wikitesto]- ^ Karl Pearson, On the dissection of asymmetrical frequency curves, 1894
- ^ UNI, Norma italiana UNI ISO 3534-1:2000, Statistica - Vocabolario e simboli, Probabilità e termini statistici generali, Milano: UNI, 2000, definizione 1.23.
- ^ Glossario Istat, su www3.istat.it (archiviato dall'url originale il 31 dicembre 2011).
- ^ Sheldon, p. 96.
- ^ UNI, Norma italiana UNI ISO 3534-1:2000, Statistica - Vocabolario e simboli, Probabilità e termini statistici generali, Milano: UNI, 2000, definizione 1.24 e 2.35.
- ^ Domenico Piccolo, Statistica, Il Mulino, Bologna, 1998, p. 123.
- ^ (EN) Joan L. Martin, Notes : Bowling Norms for College Men and Women, in Research Quarterly. American Association for Health, Physical Education and Recreation, vol. 31, n. 1, 1960-03, pp. 113–116, DOI:10.1080/10671188.1960.10613082. URL consultato il 12 giugno 2024.
Bibliografia
[modifica | modifica wikitesto]- M. Ross Sheldon, Introduzione alla statistica, 2ª ed., Maggioli Editore, 2014, ISBN 88-916-0267-1.
- Thomas H. Wannacott, Introduzione alla statistica, 19ª ed., Franco Angeli, 2009, ISBN 978-88-568-1260-2.
Voci correlate
[modifica | modifica wikitesto]- Root sum squared
- Coefficiente di variazione
- Scarto interquartile
- Varianza
- Stimatore corretto#Esempio: stimatore della varianza
- Precisione
- Median absolute deviation
- Regola 68-95-99,7
Altri progetti
[modifica | modifica wikitesto] Wikizionario contiene il lemma di dizionario «deviazione standard»
Wikizionario contiene il lemma di dizionario «deviazione standard» Wikimedia Commons contiene immagini o altri file sulla deviazione standard
Wikimedia Commons contiene immagini o altri file sulla deviazione standard
Collegamenti esterni
[modifica | modifica wikitesto]- scarto², su sapere.it, De Agostini.
- Scarto quadratico medio, in Enciclopedia della Matematica, Istituto dell'Enciclopedia Italiana, 2013.
- Deviazione standard, in Enciclopedia della Matematica, Istituto dell'Enciclopedia Italiana, 2013.
- Deviazione standard, in Dizionario di Economia e Finanza, Istituto dell'Enciclopedia Italiana, 2012.
- (EN) Opere riguardanti Standard deviations, su Open Library, Internet Archive.
- (EN) Eric W. Weisstein, Standard Deviation, su MathWorld, Wolfram Research.
- (EN) Quadratic deviation, su Encyclopaedia of Mathematics, Springer e European Mathematical Society.
- (EN) standard deviation, in Free On-line Dictionary of Computing, Denis Howe. Disponibile con licenza GFDL
- (EN) Scarto quadratico medio, su goldbook.iupac.org.
| Controllo di autorità | LCCN (EN) sh85127303 · GND (DE) 4767332-1 · J9U (EN, HE) 987007531597405171 |
|---|






























![{\displaystyle \sigma _{X}={\sqrt {\mathbb {E} [x^{2}]-(\mathbb {E} [x])^{2}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b53cf762daea0c3a0b690b854f54f517349c68d7)
![{\displaystyle \mathbb {E} [X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09de7acbba84104ff260708b6e9b8bae32c3fafa)
