Modulo proiettivo
In matematica, un modulo proiettivo è un modulo con la proprietà di essere addendo diretto di un modulo libero: ovvero P è proiettivo se esiste un modulo libero F e un suo sottomodulo N tale che F è la somma diretta di P ed N.
Questo concetto è il duale di quello di modulo iniettivo; è stato introdotto da Henri Cartan e Samuel Eilenberg nel 1956.
Definizioni equivalenti[modifica | modifica wikitesto]
Sia A un anello e P un A-modulo sinistro (definizioni totalmente analoghe possono essere date per moduli destri). La definizione precedente (P è proiettivo se è addendo di un modulo libero) può essere generalizzata: P è proiettivo se è un addendo di ogni modulo che si proietta su di esso; in termini di successioni esatte: P è proiettivo se e solo se ogni successione esatta corta
si spezza, ovvero se .
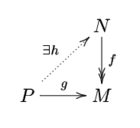
È possibile caratterizzare i moduli proiettivi anche attraverso una proprietà di sollevamento: P è un modulo proiettivo se e solo se per ogni omomorfismo suriettivo di A-moduli sinistri f : N → M e per ogni omomorfismo g : P → M esiste un omomorfismo di moduli h : P → N tale che hf = g, cioè tale da far commutare il seguente diagramma:
Altre definizioni equivalenti sfruttano maggiormente la teoria delle categorie: P è proiettivo se e solo se il funtore è esatto; usando il funtore Ext, P è proiettivo se per ogni A-modulo M.
Esempi e proprietà[modifica | modifica wikitesto]
Tutti i moduli liberi sono proiettivi; il viceversa non è in generale vero, sebbene valga per i domini ad ideali principali, per gli anelli locali e per gli anelli di polinomi in un numero finito di variabili su un dominio a ideali principali; nel caso in cui l'anello sia noetheriano e il suo spettro sia connesso, tutti i moduli proiettivi che non sono finitamente generati sono liberi.[1] Esempi di moduli proiettivi ma non liberi sono gli ideali non principali di un dominio di Dedekind, o gli ideali nella forma eA, dove e è un idempotente di A: ad esempio, se , allora e sono A-moduli proiettivi (in quanto ) ma non liberi.
Su un campo o su un corpo, tutti i moduli sono proiettivi; in generale, se tutti gli A-moduli sono proiettivi, l'anello è detto semisemplice. Questo avviene, inoltre, se e solo se tutti gli A-moduli sono iniettivi, e se e solo se la sua dimensione globale è 0.
Una somma diretta di moduli è proiettiva se e solo se lo è ogni addendo; il prodotto tensoriale di due moduli proiettivi è ancora proiettivo.
Un ideale di A è un A-modulo proiettivo se e solo se è invertibile.
Tutti i moduli proiettivi sono piatti; anche in questo caso, il viceversa non è vero. Tuttavia, tutti i moduli piatti finitamente presentati sono proiettivi.[2]
Risoluzioni proiettive[modifica | modifica wikitesto]
Una risoluzione proiettiva di un modulo M è una successione esatta
in cui ogni Pi è proiettivo; poiché ogni modulo è il quoziente di un modulo libero, ogni modulo ha una risoluzione proiettiva. Se Pk è il modulo nullo per ogni k > n, la risoluzione è detta finita; il minimo n per cui esiste una risoluzione finita
è detto dimensione proiettiva di M; se M non ha alcuna risoluzione finita, la sua dimensione proiettiva è infinita. La dimensione proiettiva misura in un certo senso quanto un modulo "è lontano dall'essere proiettivo": infatti, la dimensione proiettiva di un modulo è 0 se e solo se è proiettivo (corrispondente alla risoluzione finita ).
L'estremo superiore della dimensioni proiettive degli A-moduli è detta dimensione globale (o omologica) di A.
Note[modifica | modifica wikitesto]
- ^ Hyman Bass, Big projective modules are free, in Illinois Journal of Mathematics, 7 numero=1, 1963, pp. 24-31. URL consultato il 27 agosto 2014.
- ^ Weibel, p.71.
Bibliografia[modifica | modifica wikitesto]
- (EN) Charles A. Weibel, An introduction to homological algebra, Cambridge University Press, ISBN 0-521-43500-5.
- (EN) Pete L. Clark, Commutative Algebra (PDF). URL consultato il 5 novembre 2011 (archiviato dall'url originale il 14 dicembre 2010).
Collegamenti esterni[modifica | modifica wikitesto]
- (EN) V.E. Govorov, Projective module, in Encyclopaedia of Mathematics, Springer e European Mathematical Society, 2002.
| Controllo di autorità | LCCN (EN) sh85107381 · GND (DE) 4175892-4 · J9U (EN, HE) 987007538596705171 |
|---|