Teoria dello stato di transizione
La teoria dello stato di transizione (TST), o teoria del complesso attivato, è la teoria che tratta le velocità delle reazioni elementari assumendo un particolare tipo di equilibrio (quasi-equilibrio) tra reagenti e complessi attivati.[1]
La teoria è utilizzata soprattutto come base qualitativa per comprendere come avvengono le reazioni chimiche. La teoria dello stato di transizione ha avuto meno successo nel suo scopo originale di calcolare le costanti di velocità assoluta di reazione, in dipendenza dal fatto che il calcolo delle velocità assolute di reazione richiede una conoscenza molto accurata delle superfici di energia potenziale,[2] ma è adatta per il calcolo dell'entalpia di attivazione (ΔH‡), dell'entropia di attivazione (ΔS‡), e dell'energia libera di Gibbs di attivazione (ΔG‡) per una particolare reazione la cui costante di velocità sia stata determinata sperimentalmente.
Questa teoria fu sviluppata simultaneamente nel 1935 da Henry Eyring, allora all'Università di Princeton, e da Meredith Gwynne Evans e Michael Polanyi dell'Università di Manchester.[3][4] Prima del suo sviluppo, per determinare le energie per la barriera di reazione veniva ampiamente utilizzata la legge di Arrhenius della velocità. L'equazione di Arrhenius deriva dall'osservazione empirica e ignora ogni considerazione meccanicistica, come nel caso se uno o più intermedi di reazione siano implicati o meno nella conversione totale di un reagente in un prodotto.[5] Di conseguenza furono necessari ulteriori sviluppi per comprendere i due parametri associati a questa legge, il fattore pre-esponenziale (A) e l'energia di attivazione (ΔE‡). La teoria dello stato di transizione, che condusse all'equazione di Eyring, affrontò con successo questi due temi; tuttavia, passarono 46 anni tra la pubblicazione della legge di Arrhenius della velocità nel 1889 e l'equazione di Eyring nel 1935. Durante questo periodo di tempo il lavoro di molti scienziati e ricercatori contribuì significativamente allo sviluppo di questa teoria.
Teoria[modifica | modifica wikitesto]
I concetti fondamentali su cui si basa la teoria dello stato di transizione sono i seguenti:
- Le velocità delle reazioni sono studiate studiando i complessi attivati che si collocano al punto di sella di una superficie di energia potenziale. I dettagli di come questi complessi si siano formati non sono importanti.
- I complessi attivati sono in uno speciale equilibrio (quasi-equilibrio) con le molecole dei reagenti.
- I complessi attivati possono convertirsi nei prodotti, il che consente alla teoria cinetica di calcolare la velocità di questa trasformazione.

Sviluppo[modifica | modifica wikitesto]
Nello sviluppo della teoria dello stato di transizione furono considerati i tre approcci di seguito sintetizzati.
Trattazione termodinamica
Nel 1884, Jacobus van 't Hoff propose l'equazione di van 't Hoff per descrivere la dipendenza della costante di equilibrio dalla temperatura per una reazione reversibile:
dove ΔU è il cambiamento di energia interna, K è la costante di equilibrio della reazione, R è la costante universale dei gas, e T è la temperatura espressa in kelvin. Basandosi su un lavoro sperimentale, nel 1889, Svante Arrhenius propose un'espressione simile per la costante di velocità di una reazione:
che integrata conduce alla equazione di Arrhenius
- .
"A" venne definito fattore di frequenza (adesso chiamato coefficiente pre-esponenziale), e ΔE‡ rappresenta l'energia di attivazione. Nei primi anni del XX secolo molti accettarono l'equazione di Arrhenius, ma l'interpretazione fisica di "A" ed "E" restò vaga. Ciò condusse molti ricercatori in cinetica chimica a elaborare differenti teorie su come avvengano le reazioni chimiche, nel tentativo di correlare "A" e ΔE‡ alla dinamica molecolare direttamente responsabile delle reazioni chimiche. Nel 1910, Marcelin introdusse il concetto di energia libera di Gibbs di attivazione. La sua equazione può essere scritta come
- .
All'incirca nello stesso periodo in cui Marcelin stava lavorando sulla sua formulazione, i chimici olandesi Kohnstamm, Scheffer, e Brandsma introdussero per la prima volta l'entropia standard di attivazione e l'entalpia standard di attivazione. Essi proposero la seguente equazione per la costante di velocità:
- .
Tuttavia, la natura della costante non era stata ancora chiarita.
Trattazione teorico-cinetica
Nei primi anni 1900, Trautz e Lewis studiarono la velocità di reazione utilizzando la teoria delle collisioni, basata sulla teoria cinetica dei gas. La teoria delle collisioni tratta le molecole dei reagenti come sfere rigide che collidono l'una con l'altra; questa teoria trascura i cambiamenti di entropia.
Lewis applicò la sua trattazione alla seguente reazione e ottenne un buon accordo coi risultati sperimentali:
Tuttavia, quando successivamente la stessa trattazione venne applicata ad altre reazioni, ci furono grandi discrepanze tra i risultati teorici e quelli sperimentali.
Trattazione meccanico-statistica
La meccanica statistica ebbe un ruolo molto significativo nello sviluppo della teoria dello stato di transizione. Comunque, l'applicazione della meccanica statistica alla teoria dello stato di transizione fu sviluppata molto lentamente tenuto conto del fatto che nella metà degli anni 1800, Maxwell, Boltzmann, e Pfaundler pubblicarono diversi scritti in cui discutevano dell'equilibrio e delle velocità di reazione in termini di moti molecolari e di distribuzione statistica delle velocità molecolari.
Fu solo nel 1912 che il chimico francese A. Berthoud utilizzò la legge di distribuzione di Maxwell-Boltzmann per ottenere l'espressione per la costante di velocità
dove a e b sono costanti correlate ai termini energetici.
Due anni dopo, Marcelin diede un contributo essenziale trattando il procedere di una reazione chimica come il moto di un punto nello spazio delle fasi. Egli applicò i procedimenti meccanico-statistici di Gibbs e ottenne un'espressione simile a quella che egli stesso ottenne in precedenza da considerazioni termodinamiche.
Nel 1915, un altro importante contributo venne dal fisico britannico Rice. Basandosi sulla sua analisi statistica, concluse che la costante di velocità è proporzionale all'"incremento critico". Le sue idee furono ulteriormente sviluppate da Tolman. Nel 1919, il fisico austriaco Herzfeld applicò la meccanica statistica alla costante di equilibrio, K, e la teoria cinetica alla costante di velocità della reazione inversa, k-1, per la reazione reversibile di una molecola biatomica
- .
Ottenne la seguente equazione per la costante di velocità della reazione diretta
dove E è l'energia di dissociazione allo zero assoluto, kB è la costante di Boltzmann, h è la costante di Planck, T la temperatura assoluta, e ν è la frequenza vibrazionale del legame. Questa espressione è molto importante dato che rappresenta la prima volta in cui sia comparso il fattore kBT/h, il quale è un componente critico della teoria dello stato di transizione, in una equazione cinetica.
Nel 1920 Tolman sviluppò ulteriormente l'idea di Rice dell'incremento critico. Egli concluse che l'incremento critico (adesso definito energia di attivazione) è eguale all'energia media di tutte le molecole che partecipano alla reazione meno l'energia media di tutte le molecole di reagente.
Superfici di energia potenziale
Il concetto di superficie di energia potenziale fu molto importante nello sviluppo della teoria dello stato di transizione. Le fondamenta di questo concetto furono poste da Marcelin. Egli teorizzò che l'avanzamento di una reazione chimica potesse essere descritto come un punto in una superficie di energia potenziale con coordinate in momenti atomici e distanze.
Nel 1931, Eyring e Polanyi costruirono una superficie di energia potenziale per la reazione
- H + H2 → H2 + H.
Questa superficie è un diagramma tridimensionale basato sui principi della meccanica quantistica così come su dati sperimentali riguardanti le frequenze vibrazionali e le energie di dissociazione.
Un anno dopo il lavoro di Eyring e Polanyi, H. Pelzer e Eugene Wigner diedero un importante contributo seguendo il procedere di una reazione su una superficie di energia potenziale. L'importanza di questo contributo consistette nel fatto che fu la prima volta in cui si dibatté sul concetto di punto di sella in una superficie di energia potenziale. Arrivarono alla conclusione che la velocità di una reazione è determinata dal passaggio del sistema attraverso quella sella.
Derivazione dell'equazione di Eyring[modifica | modifica wikitesto]
L'unica importante caratteristica introdotta da Eyring, Polanyi ed Evans fu il concetto di quasi-equilibrio tra il complesso attivato e i reagenti. La velocità è quindi direttamente proporzionale alla concentrazione di questi complessi moltiplicata per la frequenza (kBT/h) con la quale essi sono convertiti nei prodotti.
Supposizione del quasi-equilibrio[6]
Si deve notare che il quasi-equilibrio è differente dal classico equilibrio chimico, ma può essere descritto utilizzando la stessa trattazione termodinamica. Si consideri la reazione
- A + B ⇄ [AB]‡ → P
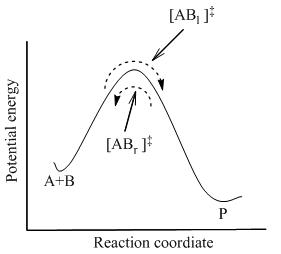
dove l'equilibrio completo viene raggiunto tra tutte le specie nel sistema inclusi i complessi attivati, [AB]‡. Tramite la meccanica statistica, è possibile calcolare la concentrazione di [AB]‡ in termini di concentrazione di A e di B.
La teoria dello stato di transizione assume che anche quando i reagenti e i prodotti non sono in equilibrio tra loro, i complessi attivati sono in quasi-equilibrio con i reagenti. Come mostrato nella figura accanto, a ogni istante di tempo, esisteranno dei complessi attivati, alcuni dei quali erano molecole dei reagenti poco prima, che sono indicate [AB→]‡ (dato che evolvono verso destra). Le restanti di loro erano molecole dei prodotti poco prima, [AB←]‡. Dato che il sistema è in completo equilibrio, le concentrazioni di [AB→]‡ e [AB←]‡ sono uguali, pertanto ogni concentrazione equivale alla metà della concentrazione totale dei complessi attivati:
- e .
Se le molecole dei prodotti vengono improvvisamente rimosse dal sistema, il "flusso" di complessi attivati che derivava dai prodotti ([AB←]‡) si fermerà; tuttavia, ci sarà ancora un flusso da sinistra verso destra. Perciò, la supposizione è che la velocità di flusso da sinistra verso destra resti inalterata dopo la rimozione dei prodotti; in altre parole, i flussi nelle due direzioni sono assunti essere indipendenti l'uno dall'altro.
Nella teoria dello stato di transizione, è importante comprendere che quando viene detto che i complessi attivati sono in equilibrio con i reagenti, ci si riferisce solamente a quei complessi attivati ([AB→]‡) che erano molecole di reagenti un istante prima.
La costante di equilibrio K‡ per il quasi-equilibrio può essere scritta come
- .
Quindi, la concentrazione dello stato di transizione AB‡ è
- .
Perciò l'equazione cinetica per la sintesi dei prodotti è
dove la costante di velocità k è data
- .
k‡ è direttamente proporzionale alla frequenza del modo vibrazionale responsabile della conversione del complesso attivato nel prodotto; la frequenza di questo modo vibrazionale è ν. Ogni vibrazione non necessariamente conduce alla formazione del prodotto, così viene introdotta una costante di proporzionalità κ, definita coefficiente di trasmissione, per tenere conto di questo effetto. In questo modo k‡ può essere riscritta come
- .
Per la costante di equilibrio K‡, la meccanica statistica conduce a un'espressione dipendente dalla temperatura che assume la forma
dove
- .
Combinando le nuove espressioni per k‡ e K‡, si può scrivere una nuova equazione per la costante di velocità:
- .
Dato che in una trasformazione isotermobarica ΔG = ΔH – TΔS, l'espressione della costante di velocità può essere espansa dando l'equazione di Eyring
- .
Le equazioni per la costante di velocità ricavate dalla teoria dello stato di transizione possono essere utilizzate per ricavare ΔG‡, ΔH‡, ΔS‡, e perfino ΔV‡ (il volume di attivazione) utilizzando dati sperimentali della velocità.
Limitazioni[modifica | modifica wikitesto]
In generale, la teoria dello stato di transizione ha fornito ai ricercatori i fondamenti concettuali per capire come avvengono le reazioni chimiche. Sebbene la teoria sia ampiamente accettata, ha delle limitazioni. Per esempio, la teoria assume che una volta che la struttura di transizione procede verso il basso lungo la superficie di energia potenziale, essa conduce a un prodotto (o a un insieme di prodotti). Tuttavia, in alcune reazioni, lo stato di transizione può attraversare la superficie di energia potenziale in un modo tale per cui esso conduce a un'inaspettata selettività di prodotto, non predetta dalla teoria dello stato di transizione (un esempio di tale reazione è la decomposizione termica dei diazobiciclopentani, esposta da Anslyn e Doughtery).
La teoria dello stato di transizione è basata anche sul presupposto che i nuclei atomici si comportino in accordo con la meccanica classica.[7] Si assume che tranne che gli atomi o le molecole non collidano con sufficiente energia per formare la struttura di transizione, la reazione non avvenga. Tuttavia, secondo la meccanica quantistica, per qualsiasi barriera con una finita quantità di energia, esiste una possibilità che le particelle possano oltrepassare tale barriera (effetto tunnel). Riguardo alle reazioni chimiche questo significa che c'è una possibilità che le molecole reagiscano persino se esse non collidono con sufficiente energia per attraversare la barriera energetica.[8] Mentre questo effetto si suppone essere trascurabile per reazioni con grandi energie di attivazione, diviene un fenomeno più importante per reazioni con barriere energetiche relativamente basse, dato che la probabilità dell'effetto tunnel aumenta al decrescere dell'altezza della barriera.
La teoria dello stato di transizione fallisce per alcune reazioni a elevata temperatura. La teoria assume che il sistema di reazione passi sopra il punto di sella a più bassa energia sulla superficie di energia potenziale. Si ricordi che il punto più elevato rappresenta lo stato di transizione. Mentre questa descrizione è coerente per reazioni che avvengono a temperature relativamente basse, a temperature elevate le molecole popolano livelli energetici vibrazionali superiori; il loro moto diventa più complesso e le collisioni possono condurre a stati di transizione lontani da quelli previsti tramite l'energia dello stato di transizione. Questa deviazione dalla teoria dello stato di transizione è osservata persino nella reazione di scambio semplice tra idrogeno biatomico e un radicale di idrogeno.[9]
Date queste limitazioni, sono state proposte diverse alternative alla teoria dello stato di transizione. Di seguito verrà data una breve descrizione di queste teorie.
Teoria dello stato di transizione generalizzata[modifica | modifica wikitesto]
Qualsiasi forma di teoria dello stato di transizione, come quella variazionale microcanonica, variazionale canonica, e quella variazionale canonica migliorata, in cui lo stato di transizione non è necessariamente localizzato sul punto di sella, viene definita "teoria dello stato di transizione generalizzata".
Teoria dello stato di transizione variazionale microcanonica
È uno sviluppo della teoria dello stato di transizione nella quale la superficie di separazione viene variata in modo che sia minimizzata la velocità calcolata per un'energia fissata. Le espressioni della velocità ottenute in una trattazione microcanonica possono essere integrate rispetto all'energia, prendendo in considerazione la distribuzione statistica sugli stati energetici, in modo da dare le velocità canoniche, o termiche.
Teoria dello stato di transizione variazionale canonica
È uno sviluppo della teoria dello stato di transizione nella quale la superficie di separazione viene variata in modo che sia minimizzata la costante di velocità a una data temperatura.
Teoria dello stato di transizione variazionale canonica migliorata
È una modificazione della teoria dello stato di transizione variazionale canonica nella quale, per energie inferiori all'energia di soglia, la posizione della superficie di separazione è considerata essere quella dell'energia di soglia microcanonica. Ciò forza i contributi alle costanti di velocità a essere uguali a zero se questi sono inferiori all'energia di soglia. Viene quindi scelta una superficie di separazione di compromesso in modo che si abbia la minimizzazione dei contributi alla costante di velocità da parte dei reagenti che possiedono energie superiori.
Note[modifica | modifica wikitesto]
- ^ (EN) IUPAC Gold Book
- ^ Truhlar, D. G.; Garrett, B. C.; Klippenstein, S. J., Current Status of Transition-State Theory, The Journal of physical chemistry, 1996, 100, (31), 12771-12800
- ^ Laidler, K.; King, C, Development of transition-state theory. The Journal of physical chemistry 1983, 87, (15), 2657
- ^ Laidler, K.; King, C, A lifetime of transition-state theory. The chemical intelligencer 1998, 4, (3), 39
- ^ Eric V. Anslyn and Dennis A. Dougherty, Transition State Theory and Related Topics in Modern Physical Organic Chemistry, University Science Books, 2006; pp 365-373
- ^ Laidler, K. J., Theories of Chemical Reaction Rates (McGraw-Hill Series in Advanced Chemistry). 1969; p 234 pp
- ^ Eyring, H.; Journal of Chemical Physics, 1935, 3, 107-115
- ^ R. Masel, Principles of Adsorption and Reactions on Solid Surfaces, New York, Wiley, 1996
- ^ Pineda, J. R., Schwartz, S. D., Philosophical Transactions of the Royal Society, B 2006, 361, pp. 1433-1438
Bibliografia[modifica | modifica wikitesto]
- Laidler, K., King, C., Development of transition-state theory, The Journal of physical chemistry, 1983, 87, (15), 2657
- Laidler, K., A lifetime of transition-state theory. The chemical intelligencer, 1998, 4, (3), 39
- Eric V. Anslyn, Dennis A. Doughtery, Transition State Theory and Related Topics in Modern Physical Organic Chemistry University Science Books, 2006; pp 365–373
- Schramm, VL., Enzymatic Transition States and Transition State Analog Design, Annual Review of Biochemistry, 1998, 67, 693-720
- Schramm, V.L., Enzymatic Transition State Theory and Transition State Analogue Design, Journal of Biological Chemistry, 2007, 282, (39), 28297-28300
- Radzicka, A., Woldenden, R., Transition State and Multisubstrate Analog Inhibitors, Methods in Enzymology, 1995, 249, 284-312
- Cleland, W.W., Isotope Effects: Determination of Enzyme Transition State Structure, Methods in Enzymology, 1995, 249, 341-373
Voci correlate[modifica | modifica wikitesto]
Collegamenti esterni[modifica | modifica wikitesto]
- (EN) Lezione sulla Teoria dello stato di transizione, su engin.umich.edu. URL consultato l'8 marzo 2009 (archiviato dall'url originale il 22 aprile 2009).








![{\displaystyle [AB_{\leftarrow }\;]^{\ddagger }={\frac {1}{2}}[AB]^{\ddagger }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9b265b12a35a355110d5754be08c2a125aba709)
![{\displaystyle [AB_{\rightarrow }\;]^{\ddagger }={\frac {1}{2}}[AB]^{\ddagger }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4601da6964dfca25301c9e8cb4041f3cbc951a90)
![{\displaystyle K^{\ddagger }={\frac {[AB]^{\ddagger }}{[A][B]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c18736a4fe5025a8d02193f02843ae0286aa5a5)
![{\displaystyle [AB]^{\ddagger }=K^{\ddagger }[A][B]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48628d3cad73d59e206efca8587dc1fcb6cd8415)
![{\displaystyle {\frac {d[P]}{dt}}=k^{\ddagger }[AB]^{\ddagger }=k^{\ddagger }K^{\ddagger }[A][B]=k[A][B]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a7b522fa1757dc08c00320e90341774c45552e4)





