Geometria descrittiva

La geometria descrittiva è la scienza che permette, attraverso determinate costruzioni geometriche, di rappresentare in modo inequivocabile su uno o più piani, oggetti bidimensionali e tridimensionali. La rappresentazione può essere finalizzata a visualizzare oggetti già esistenti, come nel rilievo (per lo più architettonico), e/o di oggetti mentalmente concepiti, come nella progettazione di manufatti tridimensionali.

I metodi di rappresentazione (di prospettiva, di assonometria e di Monge) della geometria descrittiva si basano principalmente su due operazioni fondamentali, dette operazioni di proiezione e sezione.

Gli assiomi della geometria descrittiva elementare sono sostanzialmente i postulati di Euclide, ma modificati dall'aggiunta della nozione di ente improprio (direzione, giacitura), secondo una costruzione analoga a quella della geometria proiettiva (si veda anche la voce V postulato di Euclide).

Storia

Gaspard Monge

Fin dall'antica civiltà egiziana, è stato dimostrato, attraverso il ritrovamento di disegni che illustravano copertura ellittica di tombe, un corretto utilizzo delle doppie proiezioni ortogonali. Tra il I secolo a.C. e il I secolo d.p. Vitruvio, nei suoi trattati intitolati "De architectura" usava come elementi di rappresentazione di edifici le piante ed i prospetti da lui denominati icnografie e ortografie. In epoca successiva, nell'opera di Jacopo Barozzi da Vignola "i cinque ordini di architettura", viene adoperato quello che diverrà noto come metodo di Monge. Nello stesso periodo, Alberto Dürer (1471-1528) definì alcuni procedimenti grafici riguardanti le coniche, come sezioni piane di un cono quadrico e, anche, lo studio della prospettiva. Nel 1600 gli studiosi Girard Desargues e Guarino Guarini hanno posto i fondamenti per la nascita della disciplina "geometria descrittiva", con questo nome è stata battezzata dallo scienziato francese Gaspard Monge (1746-1818). Nel 1700 fu pubblicato il libro "Geometrie descriptive" in cui vengono poste le regole fondamentali della geometria descrittiva. Regole che sono finalizzate, soprattutto, a rappresentare, su uno stesso piano (detto piano di proiezione), gli oggetti in 3D. Attualmente la geometria descrittiva comprende come parte integrante la geometria proiettiva in cui studi più significativi e conclusivi si devono a Jean Victor Poncelet (1788-1867) discepolo di Monge. Con la geometria proiettiva viene introdotto il concetto di Ente geometrico improprio (punto, retta e piano), che determina una sostanziale differenza con la geometria euclidea, pur considerando validi i rimanenti postulati di Euclide. Nel 1995 è stata codificata la Prospettiva Parallela dalla Prof.ssa Architetto Barbara Aterini, insegnante di Geometria Descrittiva alla Facoltà di Architettura dell'Università di Firenze.

Concetti

Alcuni concetti fondamentali della geometria descrittiva sono:

• definizione degli enti geometrici fondamentali (punto, retta, piano, direzione e giacitura).
• postulati d'appartenenza: di un punto ad una linea; di una linea ad una superficie; di un punto ad una superficie.
• L'incidenza: tra due rette, tra una retta ed un piano, e tra due piani; o più in generale tra linea e superfici.
  • Condizioni di parallelismo e di perpendicolarità come casi limiti di Incidenza
• Le condizioni di tangenza (in particolare la tangenza tra coniche e la tangenza tra quadriche).
• la Corrispondenza biunivoca, quali prospettività, omologia, omologia inversa, Affinità prospettiva, affinità, omotetia, Omotetia inversa ed Involuzione.

I Metodi di rappresentazione

Essi si classificano, in generale, secondo l'entità dello stabilito centro di proiezione. Quando esso è un punto proprio si parla di proiezioni centrali, altrimenti di proiezioni parallele, cioè quando tale centro di proiezione è punto improprio.

• proiezioni centrali
  • il metodo della prospettiva.
    • La restituzione prospettica (o fotorestituzione).
  • teoria delle ombre con sorgente propria (da molti non viene considerata una "teoria" in quanto si tratta sempre di una proiezione).

• proiezioni parallele.

• • proiezioni ortogonali
    • il metodo dell'assonometria
    • il Metodo di Monge
    • il metodo delle proiezioni quotate.

• • proiezioni oblique
    • il metodo dell'assonometria
  • teoria delle ombre con sorgente impropria

Problemi e costruzioni

Alcuni problemi di cui si occupa la geometria descrittiva sono:

• I problemi d'incidenza, come tra linee e superfici e come tra superfici.
• I problemi di misura delle distanze lineari (come ad esempio la costruzione geometrica che permette di determinare la distanza minima di un punto da un piano eventualmente degenere) e di quelli angolari (come ad esempio l'angolo tra retta e piano).
• costruzioni geometriche e modellazione 3D
  • delle volte
  • delle elicoidi
  • delle superfici rigate
  • delle superfici toriche
  • elicoidi
  • conoide

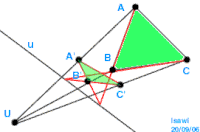
• • Raccordo tangenziale tra coniche, tra quadriche e tra toriche (vedi figura a lato)
  • Sviluppo di solidi
  • Approssimazione poliedrica di una superficie curva

Curve geometriche

• Le coniche: ottenute come sezioni piane di un cono quadrico (punto, retta, ellisse, parabola ed iperbole)
• Le quartiche: ottenute, in generale, come in intersezione di due superficie quadriche che non hanno nessuna sezione piana in comune.
• Le curve cicloidiche: curve ottenute come conseguenza del movimento planare e rigido di una conica rispetto ad un'altra conica ad essa complanare.
• Le eliche: ottenute dal movimento trasrotazionale, tridimensionale e rigido di una conica rispetto ad un'altra conica ad essa complanare.

Superfici geometriche

Le principali categorie di superfici trattate dalla geometria descrittiva sono così classificate:

• Le superfici rigate: in questa categoria vengono trattate le superfici generate dal movimento rigido di una retta lungo una o più direttrici, come gli elicoidi rigati, i conoidi rigati e le superfici coniche ed i piani (come casi particolari di rigate).

• Le superfici toriche: questa categoria include tutti i tipi di tori che sono generatI dal movimento rotatorio affine o omotetico di una conica non degenere lungo una direttrice conica, anch'essa non degenere. La condizione è che tali coniche, direttrice e generatrice, siano ortogonali tra loro.

• I paraboloidi.

Applicazioni

la geometria descrittiva viene applicata principalmente nei campi che riguardano la costruzione di manufatti architettonici. In particolare viene usata per avere proporzioni dimensionali e percettive di una data e possibile idea progettuale. L'applicazione informatica dei concetti della geometria descrittiva, permettono oggigiorno di poter creare un'architettura ad alta complessità tridimensionale, ma soprattutto di poter controllare in modo inequivocabile ogni sua forma e dimensione.

Campi d'applicazione

• Progettazione architettonica
  • Modellazione geometrica
  • Disegno tecnico
• Rilievo dell'architettura
  • Fotorestituzione 3D

Bibliografia

• Antonella Gesuele, Alessandra Pagliano, Valentina Verza. La geometria animata. Lezioni multimediali di Geometria Descrittiva. Venezia, Editrice Cafoscarina, 2007. ISBN 978-88-7543-170-9
• Lamberto Nasini. Lezioni ed esercizi di fondamenti e applicazioni di geometria descrittiva. Roma, Editrice Kappa, 1996.
• Hasan Isawi e Lamberto Nasini. Vedere con la mente. Una geometria per comprendere lo spazio senza percepirlo visivamente. Editrice Officina, 2006.
• Barbara Aterini. Introduzione ai metodi di rappresentazione della geometria descrittiva. Firenze, Alinea, 1997.

Glossario

In questa sottocategoria, della geometria descrittiva, vi sono termini e simbologie, utili a chi lavora nei vari campi di grafica, sia per facilitare il compito di individuare degli elementi notevoli di un dato oggetto geometrico, sia per acquisire un linguaggio tecnico in grado di facilitare il compito di descrivere, in modo chiaro, le situazione spaziali di tali elementi.

Voci correlate

• Geometria proiettiva
• Elemento architettonico

Altri progetti

• Commons

• Commons contiene immagini o altri file su Geometria descrittiva

Collegamenti esterni

• Trazoide. Disegno tecnico (in spagnolo) con esercizi e teoria pratica per Antonio Castilla. Dibujo técnico con ejercicios y teoría practica
• Applicazioni informatizzate della Geometria descrittiva
• geometria descrittiva, trigonometria sferica, solidi geometrici e cristallografia
• Geometria descrittiva nel Tesauro della BNCF

Portale Architettura

Portale Fotografia