Advanced Encryption Standard
| AES | |
|---|---|
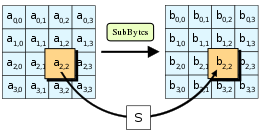 SubBytes, il primo dei quattro dell'AES. | |
| Generale | |
| Progettisti | Vincent Rijmen e Joan Daemen |
| Prima pubblicazione | 1998 |
| Derivato da | Square |
| Successori | Crypton, Anubis, GRAND CRU |
| Dettagli | |
| Dimensione chiave | 128, 192 o 256 bit |
| Dimensione blocco | 128 bit |
| Struttura | Rete a sostituzione e permutazione |
| Numero di passaggi | 10, 12 o 14 (a seconda della dimensione della chiave) |
| Migliore crittanalisi | |
| Un attacco basato sulla chiave ha forzato l'AES con una chiave a 256 bit e 9 round. Un attacco conoscendo il testo ha forzato una chiave a 192 e 256 bit con 8 round e una chiave a 128 bit con sette round. (Ferguson e altri, 2000). L'attacco XSL sembra in grado di semplificare la ricerca esaustiva. | |
In crittografia, l'Advanced Encryption Standard (AES), conosciuto anche come Rijndael ([ˈrɛindaːl]),[1][2] di cui più propriamente è una specifica implementazione,[2] è un algoritmo di cifratura a blocchi a chiave simmetrica, utilizzato come standard dal governo degli Stati Uniti d'America.
Data la sua sicurezza e le sue specifiche pubbliche si presume che in un prossimo futuro venga utilizzato in tutto il mondo come è successo al suo predecessore, il Data Encryption Standard (DES) che ha perso poi efficacia per vulnerabilità intrinseche. AES è stato adottato dalla National Institute of Standards and Technology (NIST) e dalla US FIPS PUB nel novembre del 2001[3] dopo 5 anni di studi, standardizzazioni e selezione finale tra i vari algoritmi proposti.
L'algoritmo scelto è stato sviluppato da due crittografi belgi, Joan Daemen e Vincent Rijmen, che lo hanno presentato al processo di selezione per l'AES con il nome di "Rijndael", derivato dai nomi degli inventori. Rijndael, in fiammingo, si pronuncia approssimativamente "rèin-daal".
Descrizione[modifica | modifica wikitesto]
Rijndael è un'evoluzione del primo algoritmo sviluppato da Daemen e Rijmen, Square. Square era stato sviluppato per SHARK.
A differenza del DES, Rijndael è una rete a sostituzione e permutazione, non una rete di Feistel, che implementa comunque il principio crittografico di Shannon di "confusione e diffusione". AES è veloce sia se sviluppato in software sia se sviluppato in hardware,[4] è relativamente semplice da implementare, richiede poca memoria ed offre un buon livello di protezione/sicurezza, motivi che complessivamente l'hanno preferito agli altri algoritmi proposti.
Il nuovo standard di cifratura sta sostituendo i precedenti standard e la sua diffusione continua ad aumentare. Formalmente, AES non è equivalente al Rijndael (sebbene nella pratica siano intercambiabili) dato che il Rijndael gestisce differenti dimensioni di blocchi e di chiavi. Nell'AES il blocco è invece di dimensione fissa (128 bit) e la chiave può essere di 128, 192 o 256 bit mentre il Rijndael specifica solo che il blocco e la chiave devono essere un multiplo di 32 bit con 128 bit come minimo e 256 bit come massimo.
AES opera utilizzando matrici di 4×4 byte chiamate stati (states). Quando l'algoritmo ha blocchi di 128 bit in input, la matrice State ha 4 righe e 4 colonne; se il numero di blocchi in input diventa di 32 bit più lungo, viene aggiunta una colonna allo State, e così via fino a 256 bit. In pratica, si divide il numero di bit del blocco in input per 32 e il quoziente specifica il numero di colonne.
C'è un passaggio iniziale:
AddRoundKey– Ogni byte della tabella viene combinato con la chiave di sessione, la chiave di sessione viene calcolata dal gestore delle chiavi.
Successivamente per cifrare sono previsti diversi round o cicli di processamento: ogni round (fase) dell'AES (eccetto l'ultimo) consiste dei seguenti quattro passaggi:
SubBytes– Sostituzione non lineare di tutti i byte che vengono rimpiazzati secondo una specifica tabella.ShiftRows– Spostamento dei byte di un certo numero di posizioni dipendente dalla riga di appartenenza.MixColumns– Combinazione dei byte con un'operazione lineare, i byte vengono trattati una colonna per volta.AddRoundKey– Ogni byte della tabella viene combinato con la chiave di sessione, la chiave di sessione viene calcolata dal gestore delle chiavi.
Il numero di round o cicli di processamento/elaborazione crittografica dei quattro passaggi precedenti è 10 con l'ultimo round che salta il passaggio MixColumns. A seguito la descrizione di ogni singolo passaggio.
La fase di decifratura non è identica a quella di cifratura dal momento che gli step sono eseguiti in ordine inverso. Tuttavia, si può definire un cifrario inverso equivalente ai passi dell'algoritmo usato per la cifratura, usando la funzione inversa a ogni step e un differente key schedule. Funziona siccome il risultato non cambia quando si scambiano la fase di SubBytes con quella di ShiftRows, e quella di MixColumns con una fase aggiuntiva di AddRoundKey.
SubBytes[modifica | modifica wikitesto]
Nel passaggio SubBytes ogni byte della matrice viene modificato tramite la S-box a 8 bit. Questa operazione provvede a fornire la non linearità all'algoritmo.
La S-box utilizzata è derivata da una funzione inversa nel campo finito GF(28), conosciuta per avere delle ottime proprietà di non linearità.
Per evitare un potenziale attacco basato sulle proprietà algebriche la S-box è costruita combinando la funzione inversa con una trasformazione affine invertibile.
La S-box è stata scelta con cura per non possedere né punti fissi né punti fissi opposti.

SubBytes, ogni byte della matrice è sostituito con i dati contenuti nella trasformazione S; bij = S(aij).ShiftRows[modifica | modifica wikitesto]
Il passaggio ShiftRows provvede a spostare le righe della matrice di un parametro, e dipende dal numero di riga.
Nell'AES la prima riga resta invariata, la seconda viene spostata di un posto verso sinistra, la terza di due posti e la quarta di tre.
In questo modo l'ultima colonna dei dati in ingresso andrà a formare la diagonale della matrice in uscita.
(Rijndael utilizza un disegno leggermente diverso per via delle matrici di lunghezza non fissa.)
Tutte le operazioni sono effettuate utilizzando l'indice della colonna “modulo” il numero di colonne.

ShiftRows, i byte di ogni riga vengono spostati verso sinistra dell'ordine della riga. Vedi figura per i singoli spostamenti.MixColumns[modifica | modifica wikitesto]
Il passaggio MixColumns prende i quattro byte di ogni colonna e li combina utilizzando una trasformazione lineare invertibile.
Utilizzati in congiunzione, ShiftRows e MixColumns provvedono a far rispettare il criterio di confusione e diffusione nell'algoritmo (teoria di Shannon).
Ogni colonna è trattata come un polinomio in GF(28) e viene moltiplicata modulo per un polinomio fisso .

MixColumns ogni colonna di byte viene moltiplicata per un polinomio fisso c(x).AddRoundKey[modifica | modifica wikitesto]
Il passaggio AddRoundKey combina con uno XOR la chiave di sessione con la matrice ottenuta dai passaggi precedenti (State). Una chiave di sessione viene ricavata dalla chiave primaria ad ogni round (con dei passaggi più o meno semplici, ad esempio uno shift di posizione dei bit) grazie al Key Scheduler.
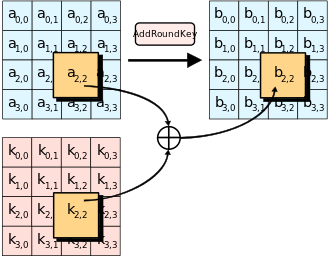
AddRoundKeys ogni byte della matrice viene combinato con la sua sottochiave tramite un'operazione di XOR.Sicurezza[modifica | modifica wikitesto]
La National Security Agency (NSA) segnalava che tutti i finalisti del processo di standardizzazione erano dotati di una sicurezza sufficiente per diventare l'AES, ma che fu scelto il Rijndael per via della sua flessibilità nel trattare chiavi di lunghezza diversa, per la sua semplice implementazione in hardware e in software e per le sue basse richieste di memoria che ne consentono un'implementazione anche in dispositivi con scarse risorse come le smart card.
L'AES può essere utilizzato per proteggere le informazioni secretate. Per il livello SECRET è sufficiente una chiave a 128 bit mentre per il livello Top secret si consigliano chiavi a 192 o 256 bit. Questo significa che per la prima volta il pubblico ha accesso ad una tecnologia crittografica che NSA ritiene adeguata per proteggere i documenti TOP SECRET. Si è discusso sulla necessità di utilizzare chiavi lunghe (192 o 256 bit) per i documenti TOP SECRET. Alcuni ritengono che questo indichi che l'NSA ha individuato un potenziale attacco che potrebbe forzare una chiave relativamente corta (128 bit), mentre la maggior parte degli esperti ritiene che le raccomandazioni della NSA siano basate principalmente sul volersi garantire un elevato margine di sicurezza per i prossimi decenni contro un potenziale attacco esaustivo.
La maggior parte degli algoritmi crittografici viene forzata riducendo il numero di round. L'AES effettua 10 round per la chiave a 128 bit, 12 round per la chiave a 192 bit e 14 round per la chiave a 256 bit. Al 2006, i migliori attacchi sono riusciti a forzare l'AES con 7 round e chiave di 128 bit, 8 round e chiave di 192 bit e 9 round e chiave di 256 bit.[5]
Alcuni crittografi hanno fatto notare che la differenza tra i round effettuati dall'AES e quelli massimi prima che l'algoritmo non sia più forzabile è ridotta (specialmente con chiavi corte). Questi temono che miglioramenti nelle tecniche di analisi possano permettere di forzare l'algoritmo senza verificare tutte le chiavi. Attualmente una ricerca esaustiva è impraticabile: la chiave a 128 bit produce 3,4×1038 combinazioni diverse. Uno dei migliori attacchi a forza bruta è stato svolto dal progetto distributed.net su una chiave a 64 bit per l'algoritmo RC5; l'attacco ha impiegato quasi 5 anni, utilizzando il tempo libero di migliaia di CPU di volontari. Anche considerando che la potenza dei computer aumenta nel tempo, servirà ancora molto tempo prima che una chiave da 128 bit sia attaccabile con il metodo forza bruta. Molte banche mettono a disposizione per l'home banking dei propri clienti chiavi a 256 bit con il risultato che si ottiene una cifratura ben 2^128 volte più sicura di quella a 128 bit sebbene quest'ultima possa considerarsi altamente sicura ed invalicabile dai moderni PC.
Un altro dubbio riguardante l'AES deriva dalla sua struttura matematica. A differenza della maggior parte degli algoritmi a blocchi, per l'AES esiste un'approfondita descrizione matematica [6]. Sebbene non sia mai stata utilizzata per condurre un attacco su misura, questo non esclude che in futuro questa descrizione non venga utilizzata per condurre un attacco basato sulle sue proprietà matematiche.
Nel 2002 l'attacco teorico chiamato attacco XSL annunciato da Nicolas Courtois e Josef Pieprzyk ha mostrato un potenziale punto debole dell'AES (e di altri cifrari). Sebbene l'attacco sia matematicamente corretto, è impraticabile nella realtà per via dell'enorme tempo macchina richiesto per metterlo in pratica. Miglioramenti nell'attacco hanno ridotto il tempo macchina richiesto e quindi, in un futuro, questo attacco potrebbe diventare attuabile. Ultimamente, alcuni esperti hanno fatto delle osservazioni agli autori dell'attacco. Sembra che abbiano commesso degli errori teorici e che, in realtà, le loro stime siano ottimistiche. Allo stato attuale, la reale pericolosità dell'attacco XSL è un punto interrogativo. Comunque, attualmente, l'AES è considerato un algoritmo veloce, sicuro e gli attacchi, fino ad ora presentati, si sono rivelati degli interessanti studi teorici ma di scarsa utilità nella pratica.
In data 1º luglio 2009 è stato pubblicato [7] un attacco correlato alla chiave migliore del metodo forza bruta su tutti i round di AES-256 e AES-192. L'attacco in questione risulta comunque, per stessa ammissione degli autori (come chiarito nelle conclusioni dello studio), essere ancora solo teoricamente realizzabile e non dovrebbe influire in alcun modo sulla sicurezza delle odierne applicazioni che fanno uso di questo cifrario. Secondo Bruce Schneier[8] comunque questa scoperta potrebbe influire negativamente sulla scelta di AES come blocco costitutivo del nuovo algoritmo di hash in fase di definizione SHA-3.
Note[modifica | modifica wikitesto]
- ^ (EN) Rijndael, su searchsecurity.techtarget.com. URL consultato il 9 marzo 2015 (archiviato dall'url originale il 12 marzo 2015).
- ^ a b (EN) Joan Daemen e Vincent Rijmen, AES Proposal: Rijndael (PDF), su csrc.nist.gov, National Institute of Standards and Technology, 9 marzo 2003, p. 1. URL consultato il 21 febbraio 2013 (archiviato dall'url originale il 5 marzo 2013).
- ^ (EN) Announcing the ADVANCED ENCRYPTION STANDARD (AES) (PDF), in Federal Information Processing Standards Publication 197, United States National Institute of Standards and Technology (NIST), 26 novembre 2001. URL consultato il 2 ottobre 2012 (archiviato dall'url originale il 12 marzo 2017).
- ^ (EN) Bruce Schneier, John Kelsey, Doug Whiting, David Wagner, Chris Hall, Niels Ferguson, Tadayoshi Kohno e Mike Stay, The Twofish Team's Final Comments on AES Selection (PDF), su schneier.com, maggio 2000 (archiviato il 2 gennaio 2010).
- ^ John Kelsey, Stefan Lucks, Bruce Schneier, Mike Stay, David Wagner, e Doug Whiting, Improved Cryptanalysis of Rijndael, Fast Software Encryption, 2000 pp. 213–230 Archived copy, su schneier.com. URL consultato il 6 marzo 2007 (archiviato il 23 febbraio 2007).
- ^ Sean Murphy
- ^ https://www.cryptolux.org/images/1/1a/Aes-192-256.pdf
- ^ Schneier on Security: New Attack on AES
Bibliografia[modifica | modifica wikitesto]
- Nicolas T. Courtois e Josef Pieprzyk, Cryptanalysis of Block Ciphers with Overdefined Systems of Equations, Springer Berlin Heidelberg, 2002, pp. 267–287, ISBN 978-3-540-00171-3.
- Joan Daemen e Vincent Rijmen, The design of Rijndael: AES - the advanced encryption standard ; with 17 tables, collana Information security and cryptography, Springer, 2002, ISBN 978-3-540-42580-9.
- Niels Ferguson, John Kelsey e Stefan Lucks, Improved Cryptanalysis of Rijndael, Springer Berlin Heidelberg, pp. 213–230, ISBN 978-3-540-41728-6.
Voci correlate[modifica | modifica wikitesto]
Altri progetti[modifica | modifica wikitesto]
 Wikibooks contiene testi o manuali sull'Advanced Encryption Standard
Wikibooks contiene testi o manuali sull'Advanced Encryption Standard Wikimedia Commons contiene immagini o altri file sull'Advanced Encryption Standard
Wikimedia Commons contiene immagini o altri file sull'Advanced Encryption Standard
Collegamenti esterni[modifica | modifica wikitesto]
- AES, in Enciclopedia della Matematica, Istituto dell'Enciclopedia Italiana, 2013.
- (EN) Gustavus J. Simmons, AES, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
- (EN) Advanced Encryption Standard, in Free On-line Dictionary of Computing, Denis Howe. Disponibile con licenza GFDL
- Criptare file e cartelle con AES (Windows), su tributemercury.com. URL consultato il 2 aprile 2012 (archiviato dall'url originale il 19 aprile 2012).
- (EN) RFC 3394 - Algoritmo AES KeyWrap
- (EN) Pronuncia di "Rijndael" (85 KB WAV file)
- (EN) Archivio del vecchio sito AES, su csrc.nist.gov. URL consultato il 5 gennaio 2005 (archiviato dall'url originale il 4 dicembre 2002).
- (EN) FIPS PUB 197: Documento con le specifiche ufficiali dell'AES (PDF file)
- (EN) Lynn Hathaway, National Policy on the Use of the Advanced Encryption Standard (AES) to Protect National Security Systems and National Security Information (PDF), su csrc.nist.gov, giugno 2003. Il C.N.S.S. annuncia l'utilizzo dell'AES per i dati classificati
- (EN) Animazione di Rijndael (SWF file)
Implementazioni[modifica | modifica wikitesto]
- Implementazione di riferimento e derivata, su embeddedsw.net.
- Un JavaScript che calcola l'AES mostrando i valori intermedi, su people.eku.edu.
- Implementazione per Python, su jclement.ca. URL consultato il 16 dicembre 2008 (archiviato dall'url originale il 21 marzo 2009).
- Implementazione per JavaScript, su cryptojs.altervista.org.

