Triangolo equilatero

Triangolo equilatero

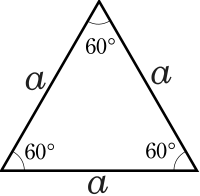
Nella geometria euclidea, un triangolo equilatero è un triangolo avente i suoi tre lati congruenti tra loro. Si dimostra che i suoi angoli sono tutti congruenti e pari a 60° = ${\frac {\pi }{3}}$rad. Poiché è sia equilatero sia equiangolo è il poligono regolare con tre lati.

I triangoli equilateri sono particolari triangoli isosceli. Tutti i triangoli equilateri sono simili tra di loro: per caratterizzare metricamente un triangolo equilatero, ovvero per caratterizzare la classe dei triangoli equilateri nel piano ottenibili gli uni dagli altri mediante traslazioni e rotazioni, serve e basta un parametro estensivo; tipicamente si usa la lunghezza dei suoi lati.

Nei triangoli equilateri, le bisettrici, le mediane, le altezze e gli assi si sovrappongono cosicché lo stesso punto rappresenta l'ortocentro, il baricentro, l'incentro e il circocentro.

Il gruppo delle simmetrie del triangolo equilatero è costituito dall'identità, dalle rotazioni intorno al suo centro di 120° e di 240° e dalle riflessioni rispetto alle bisettrici degli angoli. Tale gruppo è isomorfo al gruppo simmetrico di 3 oggetti S₃.

Costruzione

Costruzione del triangolo equilatero con riga e compasso

Come mostra Euclide in Elementi I, 1 (è la prima proposizione di tutta l'opera), il triangolo equilatero dato il lato AB si può costruire con riga e compasso in questo modo:

• Si punta il compasso in A con apertura AB e si traccia una circonferenza;
• Si punta il compasso in B con apertura BA e si traccia una circonferenza;
• Il punto d'incontro delle circonferenze C è il terzo punto cercato;
• Unendo A, B e C si ottiene un triangolo equilatero.

La dimostrazione è semplice: essendo, per definizione, tutti i punti della circonferenza equidistanti dal centro, il segmento AB è congruente ad AC, e AB è congruente a BC. Ma allora per la proprietà transitiva della congruenza, AB = AC = BC e il triangolo è equilatero.

Formule

Indicando con $l$ il lato del triangolo, con $P$ il perimetro, con $A$ l'area, con $b$ la base e con $h$ l'altezza si ha:

Perimetro

$P=l\cdot 3$

$l={\frac {P}{3}}$

Area

Errore del parser (errore di sintassi): {\displaystyle A=\frac{b \cdot ===Applicazioni del Teorema di Pitagora=== :<math> h=\sqrt{l^2-\left(\frac{l}{2}\right)^2}=\sqrt{l^2-{\frac{l^2}{4}}}=\sqrt{\frac{4l^2-l^2}{4}}=\sqrt{\frac{3l^2}{4}}=\frac{\sqrt{l^2}\cdot{\sqrt{3}}}{\sqrt{4}}=\frac{{l}\cdot{\sqrt{3}}}{2} = \frac{l}{2}\sqrt{3} }

$l={\frac {2h}{\sqrt {3}}}$

Circonferenza inscritta e circoscritta

Il centro geometrico del triangolo è il centro delle circonferenze inscritta e circoscritta al triangolo equilatero

Il raggio della circonferenza circoscritta è $R={\frac {\sqrt {3}}{3}}l$ da cui $l=R{\sqrt {3}}$

Il raggio della circonferenza inscritta è $r={\frac {\sqrt {3}}{6}}l$ da cui $R=2\cdot r$

L'area, noto R, è $A={\frac {3\cdot R^{2}}{4}}\cdot {\sqrt {3}}$

Voci correlate

• Criteri di congruenza dei triangoli
• Triangolo
• Triangolo isoscele
• Triangolo scaleno

Altri progetti

Altri progetti

• Wikimedia Commons

• Wikimedia Commons contiene immagini o altri file su triangolo equilatero