Baricentro (geometria)
| Baricentro | |
|---|---|
 | |
| Codice ETC | 2 |
| Coniugato isogonale | punto di Lemoine |
| Coniugato isotomico | se stesso |
| Coniugato cicloceviano | ortocentro |
| Complementare | se stesso |
| Anticomplementare | se stesso |
| Coordinate baricentriche | |
| λ1 | 1/3 |
| λ2 | 1/3 |
| λ3 | 1/3 |
| Coordinate trilineari | |
| x | 1/a = bc |
| y | 1/b = ac |
| z | 1/c = ab |
In geometria, il baricentro o centroide o centro geometrico di una figura bidimensionale è la "posizione media" di tutti i suoi punti, ovvero la media aritmetica delle posizioni di ciascuno di essi. La definizione si estende a qualunque figura -dimensionale in uno spazio euclideo n-dimensionale: il suo centroide è la posizione media di tutti i punti in tutte le direzioni coordinate. Se la figura presenta un iperpiano di simmetria, il centroide giace su di esso; se sono presenti più iperpiani di simmetria, il centroide giace sulla loro intersezione.
In fisica il baricentro è il punto al quale è applicata la forza risultante di tutte le forze peso parallele, può coincidere con il centro di massa di un corpo, e anche con il suo centro di gravità, ma questi tre termini non sono sempre intercambiabili. Perché il baricentro coincida con il centro di massa di un corpo, questo deve avere densità uniforme, oppure la distribuzione della materia del corpo deve avere alcune proprietà di simmetria; perché coincida con il centro di gravità, il baricentro deve coincidere con il centro di massa del corpo, che deve inoltre essere in un campo gravitazionale uniforme.
Una figura concava può avere come baricentro un punto che non appartiene alla figura stessa; ad esempio il baricentro di una falce di luna si trova in un punto del suo asse di simmetria, ma fuori dalla falce stessa.
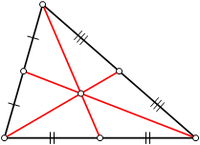
Il baricentro di un triangolo è il punto di intersezione delle sue mediane, cioè dei segmenti che uniscono ciascun vertice con il punto medio del lato opposto. Per ogni triangolo il baricentro è suo punto interno e si può dimostrare che ciascuna delle tre mediane viene divisa dal baricentro in due parti in rapporto 2:1 infatti la parte contenente il vertice è doppia rispetto all'altra.
Una situazione analoga si verifica in tre dimensioni per il baricentro di un tetraedro. Ogni segmento che unisce un vertice al baricentro della faccia triangolare opposta passa per il baricentro del tetraedro e ne viene diviso in due parti, a 3/4 della propria lunghezza a partire dal vertice.
Si può determinare sperimentalmente il baricentro di un qualsiasi oggetto solo appendendolo, dopo averlo appeso tracciamo una retta verticale passando per il centro, poi riappendiamo la stessa figura attaccandola ad un punto diverso da quello precedente (in un altro punto della figura, se prima era un lato ora prendi un angolo) e tracciamo un'altra retta verticale, il baricentro si trova nel punto di intersezione tra la prima retta e la seconda.
Coordinate cartesiane[modifica | modifica wikitesto]
Per un triangolo di vertici A(xA;yA), B(xB;yB), C(xC;yC) abbiamo:
Per un insieme finito di punti in è
Altri progetti[modifica | modifica wikitesto]
 Wikizionario contiene il lemma di dizionario «baricentro»
Wikizionario contiene il lemma di dizionario «baricentro» Wikimedia Commons contiene immagini o altri file su baricentro
Wikimedia Commons contiene immagini o altri file su baricentro
Collegamenti esterni[modifica | modifica wikitesto]
- (EN) centroid, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
- (EN) Eric W. Weisstein, Baricentro, su MathWorld, Wolfram Research.
- (EN) Proprietà caratteristiche del baricentro, su cut-the-knot.org.
- (EN) Coordinate baricentriche, su cut-the-knot.org.
- (EN) Clark Kimberling, X2, in Encyclopedia of Triangle Centers, University of Evansville, 22 ottobre 2013.





