Distribuzione di Bernoulli
| Distribuzione di Bernoulli | |
|---|---|
Funzione di distribuzione discreta 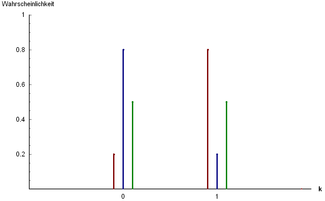 Tre esempi di distribuzioni di Bernoulli:
| |
| Funzione di ripartizione | |
| Parametri | |
| Supporto | |
| Funzione di densità | |
| Funzione di ripartizione | |
| Valore atteso | |
| Varianza | |
| Indice di asimmetria | |
| Curtosi | |
| Entropia | |
| Funzione generatrice dei momenti | |
| Funzione caratteristica | |
In teoria delle probabilità la distribuzione di Bernoulli (o bernoulliana) è una distribuzione di probabilità su due soli valori: e ,[1] detti anche fallimento e successo. Prende il nome dallo scienziato svizzero Jakob Bernoulli (1654-1705).
Definizione[modifica | modifica wikitesto]
Una variabile aleatoria discreta ha distribuzione di Bernoulli di parametro se e solo se
ossia
- per
Il valore atteso è
e la varianza è
Altre leggi[modifica | modifica wikitesto]
Un processo di Bernoulli è una successione di variabili aleatorie indipendenti di uguale distribuzione di Bernoulli , dette prove di Bernoulli. Da tale processo si possono definire le seguenti ulteriori leggi. La distribuzione binomiale descrive la probabilità del numero di successi in prove di Bernoulli, ovvero della variabile aleatoria
La distribuzione geometrica e più in generale la distribuzione di Pascal descrivono il tempo del primo e del -esimo successo rispettivamente, ovvero le variabili aleatorie e definite come
Note[modifica | modifica wikitesto]
Bibliografia[modifica | modifica wikitesto]
- Alexander M. Mood, Franklin A. Graybill, Duane C. Boes, Introduzione alla statistica, McGraw-Hill, 1991.
- Paolo Baldi, Calcolo delle probabilità e statistica, 2ª ed., McGraw-Hill, 1998, ISBN 9788838607370.
- Sheldon M. Ross, Probabilità e statistica per l'ingegneria e le scienze, Trento, Apogeo, 2003, ISBN 88-7303-897-2.
Voci correlate[modifica | modifica wikitesto]
- Distribuzione binomiale
- Distribuzione geometrica
- Distribuzione di Pascal
- Variabile casuale
- Processo di Bernoulli
Altri progetti[modifica | modifica wikitesto]
 Wikimedia Commons contiene immagini o altri file su distribuzione di Bernoulli
Wikimedia Commons contiene immagini o altri file su distribuzione di Bernoulli
Collegamenti esterni[modifica | modifica wikitesto]
- Bernoulli, distribuzione di, in Enciclopedia della Matematica, Istituto dell'Enciclopedia Italiana, 2013.
- (EN) standardized random variable, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
- (EN) Eric W. Weisstein, Distribuzione di Bernoulli, su MathWorld, Wolfram Research.







![{\displaystyle p\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33c3a52aa7b2d00227e85c641cca67e85583c43c)



























