Rapporto tra musica e matematica

Il rapporto tra musica e matematica è stato scoperto in tempi molto antichi, che risalgono al genio di Pitagora. Egli fu il primo a intuire l’esistenza di rapporti numerici tra le frequenze, e tramite questi costruì la prima scala musicale. Questo rapporto venne poi studiato da moltissimi scienziati, filosofi, musicisti quali Tolomeo, Zarlino, Galileo Galilei, Jean-Philippe Rameau, Leibniz, e altri.
Musica e matematica legate sin dall'antichità[modifica | modifica wikitesto]
L’aneddoto che racconta di come Pitagora scoprì il ponte tra musica e matematica, è tramandato da Giamblico di Calcide. Pitagora udì un giorno un fabbro che batteva martelli di pesi diversi sull’incudine. Notò che a seconda del peso variava la frequenza del suono, producendo tintinnii più o meno piacevoli. Indagando sul perché, Pitagora si rese conto che martelli i cui pesi stavano in precisi rapporti producevano suoni consonanti (piacevoli).
In laboratorio Pitagora tese delle corde elastiche (nervi di bue) tramite pesi differenti. Qui scoprì che vi era una consonanza tra coppie di suoni, quando le tensioni stavano fra loro in un rapporto di 4:1 o di 9:4. Una corda tesa da un peso quadruplo emette quindi una nota di frequenza doppia. Possiamo dire che dista un intervallo di ottava dalla precedente. Il nostro cervello percepisce le due frequenze “uguali”, ma una più acuta rispetto all’altra.
Oggi sappiamo che la frequenza fondamentale f0 del suono emesso da una corda tesa, posta in vibrazione, è direttamente proporzionale alla radice quadrata della tensione T cui la corda è sottoposta e inversamente proporzionale alla sua lunghezza L e, sotto radice, alla sua densità ρ e alla sua sezione S:
Intervalli[modifica | modifica wikitesto]
| Rapporto Lunghezze | Rapporto Pesi | Rapporto Frequenze | Intervallo (Consonante) |
| 1:2 | 4:1 | 2:1 | Ottava |
| 2:3 | 9:4 | 3:2 | Quinta |
| 3:4 | 16:9 | 4:3 | Quarta |
Un intervallo è dunque un rapporto tra le frequenze delle note considerate.
Questa proprietà vale sia “allungando” la nostra corda, sia “accorciandola”, ovvero premendo un punto della corda, posto ad un preciso rapporto di distanza. Se premiamo la corda esattamente a metà e ne pizzichiamo una delle due metà, otteniamo una nota all’ottava superiore. Nella pratica:
Se la corda libera emette la nota di riferimento “Do”, la stessa corda
- dimezzata, suona il “Do” all’ottava superiore (più acuto);
- ridotta ai suoi 3/4, suona un “Fa” (Quarta)
- ridotta ai suoi 2/3, suona un “Sol” (Quinta)
Questo procedimento è spiegato molto bene nel cortometraggio Walt Disney “Paperino nel mondo della Matemagica” (1959)
I progressi dei pitagorici arrivarono alla costruzione di una scala diatonica pitagorica. Essa era composta da sette note, prima di arrivare all’ottava nota, “uguale” alla prima ma più acuta. Il “numero” (Ottava, quinta, terza, quarta, …) assegnato all’intervallo dipende dalle note che vi si contano all’interno, facendo riferimento alla scala: DO – SOL, intervallo di Quinta, poiché da DO a SOL vi sono 5 note: DO, RE, MI, FA, SOL.
Oltre Pitagora[modifica | modifica wikitesto]
Il secondo principio per dividere l’ottava in un dato numero di parti fu ideato da Archita, tarantino di scuola greca (430-348 a.C.). Fu ripreso dai greco-latini Didimo (I sec. a.C.), e Tolomeo (83-161 d.C.), ma trovò applicazione pratica solo con l’avvento della musica tonale e con la successiva teorizzazione formulata da Gioseffo Zarlino (1517-1590) nel 1558.
Mentre il sistema pitagorico prevedeva la divisione della corda in 2, 3 o 4 parti, la novità del sistema tolemaico consisteva nella possibilità di dividere la corda in 5 e 6 parti. Si aggiunsero tra gli intervalli fondamentali anche la terza maggiore (5/4) e la terza minore (6/5). Inizialmente non fu tramandata questa scala poiché gli intervalli di terza non erano ritenuti abbastanza consonanti dai Greci.
Gli altri intervalli[modifica | modifica wikitesto]
- la seconda maggiore come differenza fra una quinta e una quarta giusta: 3/2 : 4/3 = 9/8
- la sesta maggiore come somma fra una quarta giusta e una terza maggiore: 4/3 * 5/4 = 5/3
- la settima maggiore come somma di una quinta giusta e di una terza maggiore: 3/2 * 5/4 = 15/8
I suoni che costituiscono la scala zarliniana attingono dalla serie degli armonici naturali di una nota di riferimento. Per questo motivo viene detta anche scala naturale. Tale serie può essere generata scegliendo una nota di riferimento e moltiplicandone la frequenza per 2, 3, 4 eccetera. Per riportare le note così generate nell’ambito dell’ottava di partenza si divide la loro frequenza per 2n dove n indica il numero di ottave percorse dalla nota di partenza. Infine si eliminano gli eventuali doppioni ottenuti.
La tradizione impone che le note componenti la scala diatonica siano 7:
mentre quelle che compongono la scala cromatica siano 12. Si aggiungono alle 7 note della scala diatonica naturale 5 note alterate, toccando così tutte le note possibili.
Battimenti[modifica | modifica wikitesto]

Il fenomeno dei battimenti si ha quando vengono suonate due note di frequenza simile (ma non identica). Si ha allora l'impressione di sentire un suono di frequenza vicina a quelle dei primi due, la cui intensità oscilla però nel tempo tanto più lentamente quanto più le frequenze dei primi due suoni erano ravvicinate. Per questo motivo, i battimenti sono utilizzati per determinare la presenza di note calanti o crescenti quando si intona uno strumento.
La spiegazione di questo fenomeno risiede in parte nella natura fisica delle onde sonore, e in parte nel modo in cui il nostro orecchio percepisce i suoni. Se fissiamo la nostra attenzione sulla sovrapposizione di due toni puri (tali cioè da poter essere rappresentati da onde sinusoidali) e supponendoli, per semplicità, di ampiezza uguale, possiamo applicare le formule di prostaferesi al suono risultante:
Ove si è posto
Se , (cioè se e sono vicine), si può esprimere la somma dei due suoni come un suono di frequenza intermedia, pari a , la cui ampiezza sia modulata alla frequenza molto più bassa .
Metodi di intonazione[modifica | modifica wikitesto]
Le scoperte di Pitagora mettevano in diretta relazione la nostra percezione dei suoni con grandezze misurabili (in questo caso la lunghezza della corda messa in vibrazione). In altre parole, se consideriamo i modi di vibrare (armonici) di una corda tesa fissata agli estremi e detta n la frequenza fondamentale si hanno le seguenti corrispondenze (dove f(x) indica la frequenza della nota x):
| Nota (x): | Do1 | Do2 | Sol2 | Do3 | Mi3 | Sol3 | Sib3 | Do4 |
| f(x): | n | 2n | 3n | 4n | 5n | 6n | 7n | 8n |
L'intervallo ad esempio tra Do1 e Do2 (raddoppio della frequenza), viene detto intervallo di ottava. Si noti che la parola intervallo riferito alle altezze dei suoni, si riferisce al rapporto tra le frequenze, non alla loro differenza.
Da queste si possono dedurre le frequenze da assegnare a tutte le note della scala di Do: il metodo adottato (che viene detto comunemente temperamento, anche se questo termine si riferirebbe solo ai metodi di intonazione che si discostano da quelli "naturali") ha importanti conseguenze per la costruzione degli strumenti musicali a intonazione fissa (come il pianoforte) e anche per i metodi di composizioni musicale stessi (ad esempio la dodecafonia ideata da Arnold Schönberg è una conseguenza, portata all'estremo, dell'utilizzo del temperamento equabile). Nella storia il problema del temperamento musicale è stato risolto con coerenza (almeno nella musica occidentale) solo nel XVII secolo da Andreas Werckmeister.
Intonazione pitagorica[modifica | modifica wikitesto]
Il metodo pitagorico consiste nel calcolare inizialmente il rapporto di quinta, cioè la frequenza ad esempio della nota Sol1 rispetto alla nota Do1, come segue:
Sol1: si riduce alla prima ottava Sol2 dividendone la frequenza per due, ottenendo: :
Analogamente Re1 è la quinta di Sol1 (Re2) abbassata di un'ottava: f(Re1) = f(Re2):2 =(3:2 f(Sol1)):2 = 9:8 n
Diviene ora possibile utilizzare i rapporti di quinta e ottava per ricavare le altre note della scala.
Proseguendo con questo metodo, in definitiva, la successione delle note nella scala pitagorica è definita dalla successione delle frequenze che segue (indicate in rapporto alla fondamentale):
| Nota: | Do1 | Re1 | Mi1 | Fa1 | Sol1 | La1 | Si1 | Do2 |
| Frequenza: | 1 | 9:8 | 81:64 | 4:3 | 3:2 | 27:16 | 243:128 | 2 |
Si noti che in questo modo esistono due soli intervalli (rapporti di frequenza) tra suoni consecutivi: il tono, corrispondente a 9:8, e il semitono o limma pari a 256:243.
La scala pitagorica presenta però l'inconveniente che gli intervalli adottati non si conciliano con l'esigenza di dividere l'ottava in parti proporzionali (per evitare di dover modificare l'intonazione delle singole note al cambiare della tonalità).
Intonazione naturale[modifica | modifica wikitesto]
Uno degli inconvenienti della scala pitagorica è che i rapporti di terza e sesta, utilizzando numeratori e denominatori elevati, danno luogo ad accordi poco consonanti quando sono utilizzati assieme ad altre note della scala.
Utilizzando anche gli armonici superiori, e in particolare il quinto armonico - Mi3 - della fondamentale, è possibile ottenere rapporti più consonanti, come segue:
- Mi1
- Viene ottenuto abbassando di due ottave il quinto armonico della fondamentale:
- f(Mi1) = 1/2 (1/2 (5 n)) = 5/4 n
- La1
- Si ottiene come quinta discendente di Mi2 (quinto armonico abbassato di un'ottava):
- f(La1) = 2/3 (1/2 (5 n)) = 5/3 n
- Si1
- È la quinta di Mi1:
- f(Si1) = 3/2 (5/4 n) = 15/8 n
In definitiva:
| Nota | Do1 | Re1 | Mi1 | Fa1 | Sol1 | La1 | Si1 | Do2 |
|---|---|---|---|---|---|---|---|---|
| Frequenza (scala naturale) | 1 | 9/8 | 5/4 | 4/3 | 3/2 | 5/3 | 15/8 | 2 |
| Frequenza (scala pitagorica) | 1 | 9/8 | 81/64 | 4/3 | 3/2 | 27/16 | 243/128 | 2 |
Riconducendo le note a frazioni più semplici, si ottiene anche un'ottima consonanza della sesta (La1) e migliora il rapporto con la settima maggiore (Si1). Si perde però omogeneità negli intervalli: abbiamo ora rapporti di 9/8 (tono maggiore)), 10/9 (tono minore) e 16/15 (semitono diatonico). I rapporti (intervalli) tra tono maggiore e tono minore, pari a 81/80 viene detto comma di Didimo; il rapporto tra tono minore e semitono diatonico, pari a 25/24, viene detto semitono cromatico. Si noti che in questo sistema, l'intervallo Re1-La1 (una quinta) non vale più 3/2, ma 40/27 (detto intervallo di quinta stretta). Il rapporto tra i due intervalli di quinta, che vale 80/81, è l'inverso del comma di Didimo ed è anche detto comma sintonico.
A fronte di una maggior consonanza tra le note la scala naturale introduce, quindi, un certo numero di irregolarità nella successione degli intervalli, che la rende ancora più inadatta di quella pitagorica per l'accordatura degli strumenti ad intonazione fissa (mentre è quella più vicina alle esigenze degli strumenti ad intonazione variabile).
Ciclo delle quinte[modifica | modifica wikitesto]
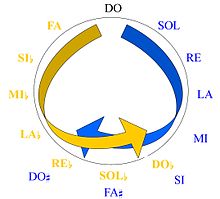
Il problema dell'intonazione, come accennato più sopra, deriva dalla necessità di poter accordare strumenti a corda come il pianoforte o gli archi in modo da poter suonare in diverse tonalità. Nessuno dei due metodi visti finora permette di risolvere con esattezza questo problema, come si può vedere dal seguente procedimento.
Un modo per accordare uno strumento ad accordatura fissa consiste nel preservare gli intervalli di quinta a partire da una corda base. In questo modo si accorda percorrendo il cosiddetto ciclo delle quinte: Do, Sol, Re, La, Mi, Si, Fa♯, Do♯, Sol♯, Re♯, La♯, Fa (o Mi♯), Do, che dopo sette ottave ritorna alla nota fondamentale. È facile vedere che nessuno dei metodi fin qui esaminati può fare sì che il Do8 coincida con quello ottenuto dal ciclo delle quinte: infatti, sia per il temperamento naturale, sia per quello pitagorico, le frequenze delle ottave sono multiple di potenze di due, mentre nel ciclo delle quinte le frequenze sono multiple di potenze di 3/2: nessuna potenza di due è anche una potenza di 3/2. Questo ragionamento vale anche per gli altri rapporti considerati.
Si vede quindi che un accordatore che volesse accordare uno strumento cercando di preservare tutti gli intervalli giusti (terze, quarte, quinte) si troverebbe di fronte ad un problema insolubile e dovrebbe comunque cercare un compromesso: è questo quanto offre il temperamento equabile.
Temperamento equabile[modifica | modifica wikitesto]


Trovare una soluzione stabile al problema del temperamento richiese diversi secoli. Oltre ai due temperamenti illustrati, ne vennero suggeriti diversi altri: ad esempio il temperamento mesotonico (detto temperamento del tono medio), che conserva gli intervalli di terza (e fu usato attorno al Rinascimento).
Un metodo alternativo a quelli finora considerati (che cercano di preservare esattamente un certo numero di intervalli razionali, oltre a quello d'ottava) è quello di imporre la divisione dell'ottava in un certo numero d'intervalli costanti. (Abbiamo visto che i temperamenti esaminati richiedono almeno due intervalli per la composizione di un'ottava). La soluzione adottata modernamente, detta sistema temperato equabile stabilisce che ogni ottava sia divisa in 12 intervalli, detti semitoni, e distribuisce le note (gradi della scala diatonica) lungo una curva logaritmica: il rapporto di ottava è fissato pari a due come di consueto. L'uso di una scala logaritmica deriva dal fatto fisiologico che il nostro orecchio percepisce come uguali intervalli tra suoni in cui è costante il rapporto tra le frequenze. Questo fatto individua una distribuzione logaritmica dei gradi rispetto alle frequenze per tutti i temperamenti fin qui esaminati: ma mentre il temperamento equabile adotta la stessa distribuzione omogenea su un intervallo di ottava, gli altri cercano di combinare sequenze di intervalli o di mantenere lo stesso intervallo senza rispettare l'intervallo di ottava.
Da quanto si è detto, è facile vedere che un intervallo di un semitono (ottenuto inserendo 12 medi geometrici tra 1 e 2) è pari a .
In questo modo, la frequenza di ogni nota corrispondente al tasto di un pianoforte è uguale alla frequenza della nota corrispondente al tasto immediatamente precedente, moltiplicata per . Dodici tasti più a destra, si giunge a una nota che ha frequenza , cioè esattamente doppia rispetto alla nota di partenza.
Questo sistema equabile stabilisce rapporti di frequenza identici a partire da qualsiasi nota individuata dalla tastiera del pianoforte (o del clavicembalo). In questo modo, si può passare da una tonalità all'altra (cioè effettuare modulazioni) senza problemi di accordatura. Le modulazioni sono appunto una caratteristica tipica della musica di Johann Sebastian Bach, che supportò l'introduzione del temperamento equabile con la raccolta "Il clavicembalo ben temperato": quarantotto preludi e fughe (due per ogni tonalità maggiore e minore) da suonarsi, appunto, su un clavicembalo accordato secondo un "buon" temperamento. In realtà il termine "temperato", all'epoca di J. S. Bach, non significava necessariamente "equabilmente temperato", ma semplicemente "con alcuni intervalli di quinta modificati (temperati)". Tra i vari temperamenti in uso a quel tempo, quello equabile era ancora lontano dall'affermarsi, anche per la difficoltà intrinseca di rendere identici tutti e dodici gli intervalli di quinta; con buona probabilità Bach usò il temperamento Werckmeister III[1].
Il metodo di costruzione del temperamento equabile fa sì che le frequenze di tutte le note possano essere espresse come:
dove è la frequenza fondamentale (tipicamente, La4 = 440 Hz) e c esprime lo scostamento da essa, espresso in cent (un'ottava contiene 1200 cent).
Il temperamento equabile, dunque, consente di avere le ottave intonate e composte tramite la ripetizione di un unico intervallo, ma ha l'inconveniente di non utilizzare nessun altro intervallo giusto. D'altra parte si può vedere come, considerando tutte le possibili divisioni dell'ottava fino a 24, si può vedere che esistono solo tre possibili suddivisioni che permettono di comporre la triade maggiore (Do, Sol, Mi) mantenendo un errore complessivo inferiore all'1%: queste sono quella in 12 (corrispondente al temperamento equabile) quella in 24 (corrispondente a una suddivisione in quarti di tono ancora nel temperamento equabile) e quella in 19, che corrisponde ad una suddivisione in terzi di tono che ha suscitato qualche interesse in passato.
A questo proposito, tramite lo sviluppo in frazione continua (i cui convergenti forniscono la successione delle migliori approssimazioni tramite rapporti di numeri interi il più piccoli possibile) del numero log23 (che è la "soluzione" del problema di ottenere un numero intero di ottave tramite successioni di quinte), si vede che il numero di suddivisioni dell'ottava che permette di avvicinarsi di più all'ideale del temperamento (cioè l'equidistanza tra i gradi), senza scostarsi troppo dalla consonanza (cioè usando valori che siano quanto più vicini possibili a rapporti di numeri piccoli) è la suddivisione in 5 gradi, oppure in 12 o in 41 o in 53, suddivisione teorizzata anche in Cina oltre che nei primi del Novecento in Europa. Un ragionamento analogo su può fare sviluppando il numero log25, che appare quando si usino le terze invece delle quinte per l'intonazione[2].
Confronto tra i metodi di intonazione[modifica | modifica wikitesto]
La tabella illustra le altezze (espresse in cent) dei gradi della scala maggiore secondo i vari metodi di intonazione.
| Grado della scala |
Temperamento equabile |
Interv. | Intonazione naturale |
Interv. | Intonazione pitagorica |
Interv. |
|---|---|---|---|---|---|---|
| I | 0 | - | 0 | - | 0 | - |
| II | 200 | 200 | 204 | 204 | 204 | 204 |
| III | 400 | 200 | 386 | 182 | 408 | 204 |
| IV | 500 | 100 | 498 | 112 | 498 | 90 |
| V | 700 | 200 | 702 | 204 | 702 | 204 |
| VI | 900 | 200 | 884 | 182 | 906 | 204 |
| VII | 1100 | 200 | 1088 | 204 | 1110 | 204 |
| VIII | 1200 | 100 | 1200 | 112 | 1200 | 90 |
Come si vede, in tutti e tre i metodi l'intervallo di ottava è identico (1200 cents) e sono praticamente uguali anche gli intervalli di quarta (498-500 cents) e di quinta (700-702 cents). Il discorso è ben diverso per gli intervalli di terza maggiore e di sesta maggiore. L'intervallo di terza maggiore naturale vale 386 cents, mentre quello pitagorico è assai crescente: 408 cents; un discorso analogo vale per la sesta. Si può dunque ben capire come mai un intervallo perfettamente consonante secondo la nostra sensibilità come quello di terza maggiore venisse considerato intollerabilmente dissonante agli inizi della polifonia, quando si usava il temperamento pitagorico: la "colpa" era insita nella costruzione pitagorica della scala.
La tabella mostra anche che le approssimazioni introdotte con il temperamento equabile sono più modeste di quelle pitagoriche (l'intervallo di terza maggiore vale 400 cents invece dei 386 cents naturali) e tali da essere ormai ampiamente tollerate. Ciò spiega come mai al nostro orecchio intervalli di terza suonino consonanti anche quando suonati al pianoforte (che è intonato secondo il temperamento equabile).
Nella seguente tabella viene riportato anche il temperamento mesotonico (o medio o del tono di mezzo), raffrontato con gli altri e le relative proporzioni pitagoriche:
| Nº semitoni | Nome intervallo | Intervallo naturale | Intervalli in cent | |||
| Temperamento equabile | Intonazione naturale | Intonazione pitagorica | Temperamento mesotonico | |||
| 0 | Unisono | 1:1 | 0 | 0 | 0 | 0 |
| 1 | Seconda minore | 16:15 | 100 | 112 | 90 | 117 |
| 2 | Seconda maggiore | 9:8 | 200 | 204 | 204 | 193 |
| 3 | Terza minore | 6:5 | 300 | 316 | 294 | 310 |
| 4 | Terza maggiore | 5:4 | 400 | 386 | 408 | 386 |
| 5 | Quarta giusta | 4:3 | 500 | 498 | 498 | 503 |
| 6 | Quarta aumentata Quinta diminuita |
45:32 64:45 |
Tritono 600 | 590 610 |
612 | 579 621 |
| 7 | Quinta giusta | 3:2 | 700 | 702 | 702 | 697 Quinta del lupo: 737 |
| 8 | Sesta minore | 8:5 | 800 | 814 | 792 | 814 |
| 9 | Sesta maggiore | 5:3 | 900 | 884 | 906 | 889 |
| 10 | Settima minore | 9:5 | 1000 | 1018 | 996 | 1007 |
| 11 | Settima maggiore | 15:8 | 1100 | 1088 | 1110 | 1083 |
| 12 | Ottava | 2:1 | 1200 | 1200 | 1200 | 1200 |
Note[modifica | modifica wikitesto]
- ^ (EN) Kyle Gann, An Introduction to Historical Tunings
- ^ (EN) Edward G. Dunne, Pianos and Continued Fractions
Bibliografia[modifica | modifica wikitesto]
- Dave Benson, Mathematics and music, Cambridge University Press (2006)
- Piergiorgio Odifreddi, Penna, pennello, bacchetta: le tre invidie del matematico, Laterza (2005), ISBN 88-420-7969-3
- G. Assayag, H.G. Feichtinger, Mathematics and music. A Diderot mathematical forum, Springer (2002)
- Andrea Frova, Fisica nella musica, Zanichelli (1999)
- Giuseppe Gerbino, Canoni ed enigmi, Torre d'Orfeo (1995)
- James Jeans, Science and music, Cambridge University Press (1937)
- Guerino Mazzola, The Topos of Music, 2nd edition (4 voll), Springer 2017
- John Pierce, La scienza del suono, Zanichelli (1987)
Voci correlate[modifica | modifica wikitesto]
- Terzo suono di Tartini
- Rapporto tra musica e informatica
- Risonanza acustica
- Scala diatonica
- Sezione aurea nella musica
- Temperamento (musica)
- Proporzione armonica
- Principio di indeterminazione tonale
- Ritmo di Euclide
Altri progetti[modifica | modifica wikitesto]
 Wikimedia Commons contiene immagini o altri file su Rapporto tra musica e matematica
Wikimedia Commons contiene immagini o altri file su Rapporto tra musica e matematica
Collegamenti esterni[modifica | modifica wikitesto]
- Nuova musica antica - Appunti di temperamento di Nicola Ferroni.
- Calcolo delle frequenze delle note, su dmr.ath.cx. URL consultato il 30 ottobre 2006 (archiviato dall'url originale il 5 ottobre 2006).
- Appunti di acustica di Marco Motta
- Math Music di Daniele Trucco









![{\displaystyle {\sqrt[{12}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc835f27425fb3140e1f75a5faa35b1e8b9efc35)
![{\displaystyle {\sqrt[{12}]{2}}^{12}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6fe6d690dfd6df140405ecb352b1b6b031210538)

