Battimenti (musica)

La curva inviluppo del battimento

Battimento

Nella teoria musicale, in fisica e particolarmente in acustica, il battimento è la frequenza risultante dalla sovrapposizione di grandezze periodiche, in genere oscillazioni sinusoidali di diversa e vicina frequenza. Si basa sulle proprietà del principio di sovrapposizione. Oltre ai campi citati, tutti i fenomeni fisici che prevedono onde risentono del fenomeno del battimento, onde meccaniche ed onde elettromagnetiche comprese; battimenti si verificano, tra l'altro, in materia di elaborazione dei segnali, quando due frequenze di segnale si trovano vicine le une alle altre.

Descrizione

Entrando più nel dettaglio del fenomeno acustico, al battimento risulta un effetto vibratorio particolare, caratterizzato da rapide ondulazioni acustiche. L'effetto è un rafforzamento seguito da un indebolimento del suono a seconda che le frequenze siano in concordanza o in discordanza di fase. I battimenti si distinguono con difficoltà negli strumenti a corde percosse come il pianoforte, a causa della breve durata dei suoni. Si rileva con minore difficoltà negli strumenti a vento ed a serbatoio d'aria, come ad esempio l'organo, in quanto hanno una sonorità più ampia. Questo effetto è anche facilmente riscontrabile nel cosiddetto vibrato degli archi. Infatti, siccome il vibrato si ottiene spostando leggermente il dito sulla corda del violino, esso causa dei suoni leggermente diversi l'uno dall'altro determinando, con la sovrapposizione delle vibrazioni, i battimenti.

Approccio fisico

Battimenti tra due suoni con una differenza in frequenza pari all'1%

Supponiamo di avere due corpi che vibrano simultaneamente, i cui suoni si possano rappresentare con onde sinusoidali con la stessa frequenza e la stessa ampiezza. Queste due onde possono sovrapporsi in diverse maniere: in fase (interferenza costruttiva), in opposizione di fase (interferenza distruttiva), o in una via di mezzo. Essendo il suono risultante la somma dei due suoni, nel primo caso questo sarà identico ai primi due, ma di ampiezza doppia (le creste si sommano e le valli si sommano); nel secondo caso non si avrà alcun suono risultante (le creste e le valli si compensano in ogni punto annullandosi tra di loro); nel terzo si avrà un suono di intensità intermedia, a seconda di quanto è lo sfasamento tra i due suoni iniziali. Naturalmente, avendo i due suoni la stessa frequenza, lo sfasamento sarà costante nel tempo: se ad esempio la prima cresta del primo suono è perfettamente sovrapposta alla prima cresta del secondo, lo stesso avverrà per le seconde creste, per le terze e così via (analogamente nel caso di sfasamento arbitrario).

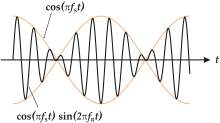
Supponendo ora che le due frequenze non siano proprio identiche, ma che ci sia una piccola differenza tra di esse, lo sfasamento questa volta non sarà più costante, ma varierà nel tempo: se ad esempio le prime creste dei due suoni coincidevano perfettamente (l'intensità totale quindi era il doppio), le seconde non saranno perfettamente sovrapposte, perché una arriverà un po' prima dell'altra; per le terze creste questa differenza di fase sarà ancora più marcata e così via, fino a quando la cresta del primo suono non sarà sovrapposta a una valle del secondo: i due suoni sono passati in opposizione di fase e l'intensità totale è zero. Procedendo ancora in maniera analoga, dopo un certo numero di periodi (dipendente dalla differenza relativa tra le due frequenze iniziali) i due suoni ritorneranno in fase. In altri termini si hanno battimenti quando lo sfasamento (e quindi il tipo di interferenza) tra due suoni di frequenze simili varia nel tempo. Questo meccanismo si vede chiaramente nell'immagine.

Un'elegante spiegazione matematica del fenomeno si dà tramite le formule di prostaferesi: se rappresentiamo i due suoni con due onde sinusoidali di ampiezza unitaria (per semplicità), possiamo applicare le formule al suono risultante:

$\sin(\omega _{1}t)+\sin(\omega _{2}t)=2\cos \left({\frac {\omega _{1}-\omega _{2}}{2}}t\right)\sin \left({\frac {\omega _{1}+\omega _{2}}{2}}t\right)=2\cos \left(\Omega t\right)\cdot \sin \left(\omega t\right)$

Ove si è posto $\omega ={\frac {\omega _{1}+\omega _{2}}{2}}$, $\Omega ={\frac {\omega _{1}-\omega _{2}}{2}}$.

Se $\Omega \ll \omega$, (cioè se $\omega _{1}$ e $\omega _{2}$ sono vicine), si può esprimere la somma dei due suoni come un suono di frequenza intermedia, pari a $\omega$, la cui ampiezza sia modulata alla frequenza molto più bassa $\Omega$.

Esempi pratici di battimenti

Il fenomeno dei battimenti è facilmente riscontrabile se facciamo vibrare contemporaneamente due corpi che hanno fra loro una leggera differenza di frequenza (per esempio di una sola vibrazione al secondo), nel primo istante i due moti arriveranno all'orecchio nella stessa fase di vibrazione; ma dopo mezzo secondo la prima origine sonora avrà compiuto mezza vibrazione in più della seconda e i due moti saranno in fase opposta. Nel successivo mezzo secondo le vibrazioni si rimetteranno gradatamente in fase e l'orecchio riceverà nuovamente due moti concordi.

Canale sinistro: La3 220 Hz Canale destro: Sol#3 207.65 Hz Frequenza di battimenti: 12.35 Hz (Alta frequenza)

Frequenza a 2Hz che emerge dai toni a 220 e 222 Hz (Bassa Frequenza)

L'intensità del suono quindi, nell'alternarsi delle diverse fasi oscillerà continuamente, sì che nel miscuglio dei due suoni, leggermente disuguali d'altezza, si avrà, ad intervalli uguali, un susseguirsi di periodici rinforzamenti e di periodici indebolimenti che sono chiamati battimenti. Vi sono degli strumenti che producono quasi sempre dei battimenti: così sono le campane che, presentando diversità di spessore in diversi punti, producono battimenti assai intensi che conferiscono loro la caratteristica sonorità ondulante. Spesso i battimenti sono appositamente impiegati per conseguire effetti speciali; nell'esempio dell'organo, il registro della voce umana è formato da due canne non perfettamente intonate, allo scopo di ottenere una specie di tremolio che imita la voce dei cantanti. Anche la voce celeste è ottenuta da due canne intonate in modo da ottenere questo effetto.

Suoni di differenza, addizione

Suonando due note contemporaneamente, l'orecchio percepisce note aggiuntive di varie frequenze pari ad opportune somme e differenze delle due note emesse: si parla in questi casi di suoni di combinazione. Fra questi il più importante da un punto di vista pratico è il cosiddetto terzo suono di Tartini, scoperto appunto dal Tartini nel ‘700. Il celebre violinista constatò infatti che suonando un bicordo ad un intervallo di 5ª (ovvero con rapporto di frequenze 3:2) si sentiva al basso un'altra nota la cui frequenza corrispondeva a un numero di vibrazioni pari alla differenza fra quelle dei due suoni originari. Così, ad esempio, se un suono aveva 900 vibrazioni e l'altro 600, il suono ulteriore che si sentiva aveva 300 vibrazioni al secondo ed era, quindi, di un'ottava più grave di quest'ultimo.

Da un punto di vista fisico il fenomeno risulta particolarmente evidente suonando due note ad un intervallo di 5ª poiché i prodotti di intermodulazione (vedi nel seguito) del second'ordine f₂−f₁ e del terz'ordine 2f₁−f₂, che sono normalmente disgiunti, in questo caso coincidono esattamente sommandosi.

Il fenomeno dei suoni di combinazione è ormai noto da oltre mezzo secolo nell'elettronica applicata alle telecomunicazioni dove questi vengono denominati "prodotti di intermodulazione": si generano in ogni amplificatore non lineare, ovvero che produce una distorsione sui segnali in ingresso, in particolare quindi anche all'interno del nostro orecchio quando questo percepisce due suoni da sorgenti distinte.

Due suoni di frequenza $f_{1}$ ed $f_{2}$ sommati in un amplificatore non lineare come il nostro orecchio, producono infatti i prodotti di intermodulazione del second'ordine: $f_{1}+f_{2},\,f_{2}-f_{1}$; del terz'ordine: $2f_{1}+f_{2},\,2f_{1}-f_{2},\,2f_{2}+f_{1},2f_{2}-f_{1}$ e degli ordini successivi; oltre alle armoniche $2f_{1},\,2f_{2},\,3f_{1},\,3f_{2}$... multiple delle frequenze fondamentali. Sono tali frequenze generate all'interno dell'orecchio a produrre i suoni differenza e addizione, i primi a lungo confusi con inesistenti "armonici inferiori" o "ipotoni".

Termini come "ipotoni", "suoni di moltiplicazione", "subarmonici", che si trovano sovente in letteratura non hanno alcun significato in fisica. Il fenomeno dei cosiddetti subarmonici, ad esempio, deriva non tanto da un fenomeno fisico reale, quanto da un errore indotto dall'orecchio quando percepisce due suoni da sorgenti distinte producendo al proprio interno i prodotti di intermodulazione sopra citati.

Applicazioni pratiche

Il fenomeno del "terzo suono" trova una sua applicazione pratica nella costruzione degli organi: talvolta, invece di costruire canne enormi per frequenze molto basse si creano registri in cui due canne a distanza di quinta suonano contemporaneamente creando l'illusione di un terzo suono più profondo; tali registri sono spesso riconoscibili per il loro nome, solitamente Acustico, Risultante o Gravissima. Anche il theremin sfrutta il battimento tra due frequenze non udibili (nel campo degli ultrasuoni) per ottenere un suono udibile e modulabile cambiando la frequenza di una delle due onde.

I registri di Voce umana, Voce celeste, Unda maris, Voce eterea, Timballi degli organi e molti registri delle fisarmoniche (il registro "musette" tipico della musica francese e del liscio) sfruttano il fenomeno dei battimenti per ottenere un suono più caldo ed espressivo. Questi registri fanno suonare contemporaneamente due canne (o ance): una intonata correttamente ed una leggermente calante o crescente, in modo da ottenere un certo numero di oscillazioni di intensità al secondo.

Interessante segnalare che nella pratica operativa dell'accordatura di strumenti musicali gli accordatori non sfruttano i battimenti che si verificano tra i fondamentali ma quelli tra alcuni loro armonici facilmente percepibili. Così ad esempio se vengono suonati in concomitanza un Do3 e un Sol3, il terzo suono armonico del Do3 che è un Sol4 "batte" col secondo armonico del Sol3 che è appunto lo stesso Sol4. In base alla frequenza dei battimenti di questi suoni armonici comuni coincidenti si sono realizzate e si realizzano le accordature dette impropriamente "ad orecchio" ma che hanno un profondo connotato scientifico basato sulle leggi della spettroscopia acustica. Le accordature storiche quali la pitagorica e mesotonica, ad esempio, potevano essere effettuate sfruttando le caratteristiche timbriche degli strumenti. Un pianoforte ad esempio non potrà mai essere accordato per terze, proprio perché è impossibile percepire i battimenti tra il quinto armonico del fondamentale (es. Do3) con il quarto armonico della terza (Mi3), cosa invece possibile per un organo o un clavicembalo, tentativi sperimentali nell'accordatura di un pianoforte col sistema mesotonico dove si utilizzano ben otto intervalli di terza maggiore (5/4) portano ad innumerevoli imprecisioni nella realizzazione degli otto intervalli stessi e nella conseguente realizzazione della quinta del lupo che costituisce il processo operativo finale dell'accordatura stessa. In sostanza, storicamente è stato possibile ideare e conseguentemente realizzare certe accordature perché le caratteristiche timbriche (percezione dei suoni armonici) dei vari strumenti consentivano agli accordatori di poterle realizzare con una certa facilità

Intorno al 1965 Pietro Grossi, pioniere della computer music registra un repertorio di eventi sonori nello Studio di Fonologia Musicale di Firenze S 2F M, tra cui una serie di Battimenti. Lo scopo era creare del materiale sonoro da utilizzare per altre composizioni. I Battimenti però, possono essere ascoltati anche come opera compiuta, tanto che alcuni, come Albert Mayr uno dei maggiori collaboratori di Grossi all'epoca dello studio S 2F M di Firenze, si sbilanciano definendoli come una delle opere più affascinanti del secolo scorso,per la massima espressività pur nell'essenzialità del suono.

Nel 2019 le frequenze dei Battimenti di Grossi vengono riprese dal musicista Sergio Maltagliati e dal pittore astrattista Romano Rizzato. Maltagliati usa 11 frequenze di suoni, da 395 a 405 Hz (le stesse registrate da Grossi), combinate in base a quanto suggerisce la pittura di Rizzato.

Toni binaurali

I toni binaurali sono dei battimenti che vengono generati direttamente dal cervello quando le due onde sonore vengono ascoltate separatamente tramite degli auricolari (quindi non vi è sovrapposizione fisica delle due onde sonore).

Bibliografia

• Alfredo Ferraro, Enciclopedia della radio, Firenze, Sansoni, 1954, vol. 1, p. 175.

Voci correlate

• Rapporto tra musica e matematica

Altri progetti

Altri progetti

• Wikimedia Commons

• Wikimedia Commons contiene immagini o altri file su Battimenti

Collegamenti esterni

• [1], Università di Modena e Reggio Emilia, con esempi ascoltabili.

Controllo di autorità	GND (DE) 4267871-7