Minimax

Il minimax, nella teoria delle decisioni, è un metodo per minimizzare la massima (minimax) perdita possibile; in alternativa, per massimizzare il minimo guadagno (maximin). Fu scoperto nella teoria dei giochi in caso di gioco a somma zero con due giocatori, sia nel caso di mosse alternative (turni) sia di mosse simultanee, venendo successivamente esteso a giochi più complessi e al supporto decisionale in presenza di incertezza.
Una versione semplice dell'algoritmo si può vedere in giochi come il tris, dove è possibile vincere, perdere o pareggiare.
- Se il giocatore A può vincere con una sola mossa, la mossa migliore è quella vincente.
- Se il giocatore B sa che una data mossa porterà A a poter vincere con la sua prossima mossa, mentre un'altra lo porterà a pareggiare, la migliore mossa del giocatore B è quella che lo porterà alla patta.
Verso la fine del gioco è facile capire quali sono le mosse migliori; l'algoritmo minimax trova la mossa migliore in un dato momento cercandola a partire dalla fine del gioco e risalendo verso la situazione corrente. Ad ogni passo l'algoritmo assume che il giocatore A cerchi di massimizzare le sue probabilità di vincere, mentre B cerchi di minimizzare le probabilità di vittoria di A, per esempio massimizzando le proprie chance di vittoria.
Il criterio Minimax nella teoria statistica delle decisioni[modifica | modifica wikitesto]
Nella classica teoria delle decisioni statistica, il minimax è uno stimatore che usiamo per stimare un certo valore , per noi importante; fra tutti i possibili , quello minimax deve minimizzare la massima perdita possibile, cioè deve godere della seguente proprietà:
- .
dove è lo stimatore minimax e è una funzione di rischio, che è definita come l'integrale di una corrispondente funzione di perdita.
Algoritmi minimax in giochi a turni[modifica | modifica wikitesto]
Nei giochi a turni (N giocatori muovono o giocano alternativamente), il principio del minimax assume la forma di algoritmo minimax, cioè un algoritmo ricorsivo per la ricerca della mossa migliore in una determinata situazione. L'algoritmo minimax è costituito da una funzione di valutazione posizionale che misura la bontà di una posizione (o stato del gioco) e indica quanto è desiderabile per il dato giocatore raggiungere quella posizione; il giocatore fa poi la mossa che minimizza il valore della migliore posizione raggiungibile dall'altro giocatore. Quindi l'algoritmo minimax assegna un valore ad ogni mossa legale, proporzionale a quanto essa diminuisce il valore della posizione per l'altro giocatore.
Quale valore venga realmente assegnato dipende da come vengono valutate le posizioni finali di vittoria e di sconfitta: un metodo è assegnare 1 alle mosse che portano alla vittoria finale e -1 a quelle di sconfitta (il che porta a sviluppare la teoria combinatoria dei giochi formulata da John Conway), un altro è di adottare i valori infinito positivo e negativo. Il valore per il giocatore A di ogni mossa non immediatamente vincente è poi il valore minimo di tutte le possibili contromosse di B. Per questo A viene anche detto "giocatore massimizzante" e B "giocatore minimizzante".
Questo presuppone che sia possibile per chi computa (non parliamo ancora di applicazioni al calcolatore) valutare tutto l'albero delle mosse possibili del gioco; in realtà questo si può fare solo per giochi molto semplici, mentre per altri, come gli scacchi o il go questo non è possibile o lo è solo nelle fasi finali, e in generale si può solo calcolare una stima della probabilità che una data mossa porti alla vittoria di uno dei giocatori.
Il calcolo di questa stima può essere migliorato se è possibile fornire una funzione di valutazione euristica che valuti le posizioni non terminali del gioco senza dover conoscere tutte le mosse successive: in questo caso si possono considerare solo un certo numero di mosse future. Questo numero è detto "profondità" dell'algoritmo ed è misurato in mosse: Deep Blue ha una profondità di 12 mosse[senza fonte].
In pratica il lavoro dell'algoritmo minimax è di esplorare tutti i possibili nodi dell'albero di gioco: il numero medio di nodi figlio per ogni nodo in esame è detto fattore di diramazione, ed è pari al numero medio di mosse possibili in una generica posizione del gioco. Pertanto il numero di nodi da valutare cresce esponenzialmente con la profondità di ricerca ed è pari al fattore di diramazione elevato alla profondità di ricerca. La complessità computazionale dell'algoritmo minimax quindi è NP completa, il che lo rende poco pratico per ottenere una soluzione definitiva di giochi meno che banali, e utile solo per ottenere una condotta di gioco "non troppo cattiva". Tuttavia le prestazioni del minimax possono essere migliorate drasticamente, mantenendo la correttezza dei risultati, adottando la potatura alfa-beta: esistono altri metodi euristici di potatura dell'albero di gioco, ma questo è l'unico che non influenza il risultato finale della ricerca minimax.
Pseudocodice[modifica | modifica wikitesto]
Ecco uno pseudocodice di algoritmo minimax, con una profondità euristica specificata:
function minimax(nodo, profondità)
SE nodo è un nodo terminale OPPURE profondità = 0
return il valore euristico del nodo
SE l'avversario deve giocare
α := +∞
PER OGNI figlio di nodo
α := min(α, minimax(figlio, profondità-1))
ALTRIMENTI dobbiamo giocare noi
α := -∞
PER OGNI figlio di nodo
α := max(α, minimax(figlio, profondità-1))
return α
Esempio[modifica | modifica wikitesto]
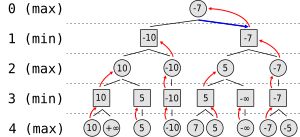
Supponiamo di avere un gioco in cui i due giocatori hanno solo due mosse possibili ciascuno ogni turno. L'algoritmo genera l'albero di gioco a destra, dove i cerchi rappresentano le mosse del giocatore che usa l'algoritmo (giocatore massimizzante) e i quadrati sono le mosse dell'avversario (giocatore minimizzante). Per le limitazioni del sistema di calcolo, come spiegato sopra, limitiamo l'albero a una profondità di quattro turni.
L'algoritmo valuta ogni nodo foglia con una funzione di valutazione euristica e ottiene i valori mostrati. Le mosse che fanno vincere il giocatore massimizzante hanno un valore infinito positivo, mentre le mosse che danno la vittoria al giocatore minimizzante hanno un valore infinito negativo. Al terzo livello l'algoritmo sceglierà, per ogni nodo, il nodo figlio con il valore minore ed assegnerà tale valore al nodo in esame; per esempio il nodo a sinistra assumerà il valore minimo fra "10" e "+∞", cioè "10". Il prossimo passo, al livello 2, sceglie il massimo valore fra tutti i nodi figli (i nodi del livello 3) e lo assegna al rispettivo nodo genitore del secondo livello. L'algoritmo continua a valutare i valori massimi e minimi dei nodi figli e ad assegnarli ai nodi genitori, alternativamente, finché non raggiunge il nodo radice dell'albero, per il quale sceglie il nodo figlio con il valore massimo (rappresentato con una freccia blu in figura). Questa mossa è quella che il giocatore dovrebbe fare per minimizzare la massima possibile funzione di perdita.
Teorema minimax nel caso di mosse simultanee[modifica | modifica wikitesto]
Il seguente è un esempio di gioco a somma zero, dove A e B muovono contemporaneamente, che illustra l'algoritmo minimax. Supponiamo che ogni giocatore possa scegliere fra tre mosse possibili e la matrice ricompensa per A sia:
| B sceglie B1 | B sceglie B2 | B sceglie B3 | |
|---|---|---|---|
| A sceglie A1 | +3 | -2 | +2 |
| A sceglie A2 | -1 | 0 | +4 |
| A sceglie A3 | -4 | -3 | +1 |
mentre B ha la stessa matrice ricompensa ma con i segni invertiti (cioè se le scelte sono A1 e B1 allora B paga 3 ad A) allora la scelta minimax semplice per A è A2, perché così il peggior risultato possibile sarebbe di pagare 1, mentre quella per B è B2 perché il risultato peggiore sarebbe di non pagare nulla. Tuttavia questa soluzione non è stabile, perché se B pensa che A sceglierà A2 allora B giocherà B1 per guadagnare 1; perciò se A crede che B scelga B1, A giocherà A1 per guadagnare 3, che porterà B a giocare B2, portando entrambi i giocatori a rendersi conto della difficoltà di fare una scelta. Per questo è necessaria una strategia più solida.
Alcune mosse sono dominate dalle altre e possono essere eliminate: A non giocherà mai A3 perché il risultato sarebbe peggiore degli altri casi, a prescindere da cosa giocherà B; B non giocherà comunque B3, perché B2 darà un risultato migliore qualunque sarà la scelta di A.
A può evitare di dover pagare in futuro più di 1/3 giocando A1 con probabilità 1/6 e A2 con probabilità 5/6, senza considerare le giocate di B. B può assicurarsi un guadagno certo di almeno 1/3 con una strategia casuale, giocando B1 con probabilità 1/3 e B2 con probabilità 2/3, a prescindere dalle mosse di A. Queste due strategie minimax miste sono stabili e non ulteriormente migliorabili.
John von Neumann dimostrò il Teorema minimax nel 1928, stabilendo che tali strategie esistono sempre in giochi di due giocatori a somma zero, e possono essere trovate risolvendo un opportuno sistema di equazioni.
Minimax in situazioni di incertezza[modifica | modifica wikitesto]
La teoria del minimax è stata estesa anche alle decisioni: cioè situazioni in cui non ci sono avversari, ma l'esito finale di una scelta dipende da fattori sconosciuti e/o imprevedibili, per esempio scegliere dove fare prospezioni geologiche in cerca di minerali: ogni ricerca ha un costo, che viene perso se non si trova nulla ma viene ripagato di molte volte se si trova un filone sfruttabile. Un possibile approccio è trattare questi casi come un gioco contro la Natura e usare un atteggiamento simile alla Legge di Murphy e cercando di minimizzare il costo totale massimo, con le stesse tecniche dei giochi a due giocatori a somma zero. Per queste situazioni (giochi a due giocatori in cui interviene anche la casualità) sono stati ideati gli alberi expectiminimax.
Il principio minimax nei giochi non a somma zero[modifica | modifica wikitesto]
Se gli scambi fra i giocatori non sono a somma zero, l'applicazione del principio del minimax sembra portare a strategie non ottimali. Per esempio nel gioco del dilemma del prigioniero la strategia minimax per ogni prigioniero è di tradire sempre, mentre la strategia ottimale è non tradire mai. Pertanto, in questa categoria di giochi la strategia migliore non è necessariamente minimax.
Applicazioni[modifica | modifica wikitesto]
Etica[modifica | modifica wikitesto]
Il filosofo John Rawls ha argomentato nel suo libro A Theory of Justice che se si pone un individuo dietro un "velo di ignoranza" (la cosiddetta posizione originale) sulla propria situazione esistenziale, egli formulerà il concetto di società giusta usando il principio del minimax. Secondo questo principio, gli individui dovrebbero scegliere il tipo di società che offre "il miglior caso peggiore", cioè in cui gli individui più sfortunati siano nella condizione meno disperata.
Bibliografia[modifica | modifica wikitesto]
- John von Neumann [1928]: Zur Theorie der Gesellschaftsspiele, Matematische Annalen, 100, 295-320; traduzione inglese: On the Theory of Games of Strategy, in "Contributions to the Theory of Games", n. IV, 13-42, 1959; vedi anche "Collected Works", vol. VI.
Voci correlate[modifica | modifica wikitesto]
- John von Neumann
- Tabella di trasposizione
- Tabella di refutazione
- Effetto orizzonte
- Negamax
- Expectiminimax
- Potatura alfa-beta
- Claude Elwood Shannon
Collegamenti esterni[modifica | modifica wikitesto]
- Minimax, in Dizionario delle scienze fisiche, Istituto dell'Enciclopedia Italiana, 1996.
- Mìnimax, su Vocabolario Treccani, Istituto dell'Enciclopedia Italiana.
- minimàssimo, su sapere.it, De Agostini.
- Minimax, in Enciclopedia della Matematica, Istituto dell'Enciclopedia Italiana, 2013.
- (EN) mini-max theorem, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
- (EN) minimax, in Free On-line Dictionary of Computing, Denis Howe. Disponibile con licenza GFDL
- Minimassimo, in Grande Dizionario di Italiano, Garzanti Linguistica.
- (EN) The Minimax Theorem, su cut-the-knot.org.
- (EN) Minimax Analysis for Zero Sum Games, su geocities.com. URL consultato il 5 maggio 2007 (archiviato dall'url originale l'11 novembre 2007).
- (EN) "Maximin principle" from A Dictionary of Philosophical Terms and Names., su swif.uniba.it. URL consultato il 5 maggio 2007 (archiviato dall'url originale il 7 marzo 2006).
- (EN) Play a betting-and-bluffing game against a mixed minimax strategy, su bewersdorff-online.de.
- (EN) The Dictionary of Algorithms and Data Structures entry for minimax, su nist.gov.
- Strategy Game Programming, su fierz.ch. — Strategy Game Programming for board games such as Checkers and Chess




