Effetto Zeeman

L'effetto Zeeman è un fenomeno che consiste nella separazione delle linee spettrali a causa di un campo magnetico esterno. Si osserva che ciascuna riga si scinde in più righe molto vicine, a causa dell'interazione del campo magnetico con i momenti angolare e di spin degli elettroni. L'effetto Stark-Lo Surdo rappresenta l'analogo fenomeno in relazione alla presenza di un campo elettrico esterno. L'effetto Zeeman si rivela particolarmente importante in spettroscopia e in particolare per la EPR e la NMR.

Quando le linee spettrali sono rappresentate da linee di assorbimento, l'effetto viene chiamato effetto Zeeman inverso.

Il nome è dovuto al fisico olandese Pieter Zeeman, che per primo scoprì tale effetto nel 1896 ricevendo anche il premio Nobel per la fisica nel 1902.

Introduzione

Separazione delle linee spettrali causata dall'effetto Zeeman. Senza la presenza di un campo magnetico, le configurazioni a, b, e c possiedono la medesima energia, così come d, e ed f. La presenza di un campo magnetico provoca la separazione dei livelli energetici: quella che prima era una singola linea legata alla transizione da a, b o c a d, e o f diverrà un insieme di linee legate alla particolare transizione coinvolta. Ovviamente non tutte le transizioni sono permesse, in accordo con le regole di selezione.

Separazione di due singole linee spettrali a causa dell'effetto Zeeman

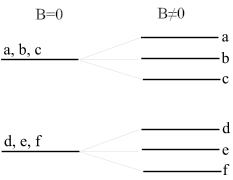
Nella maggior parte degli atomi, esistono diverse configurazioni elettroniche che possiedono la medesima energia, quindi le transizioni tra differenti coppie di configurazioni corrispondono a una singola linea spettrale. La presenza di un campo magnetico esterno elimina la degenerazione dei livelli energetici, interagendo in modo differente con gli elettroni in funzione dei differenti numeri quantici e modificando leggermente le loro energie. Il risultato è che da differenti configurazioni che possiedono la stessa energia si ottengono energie leggermente diverse, che producono linee spettrali molto ravvicinate. Dato che la distanza tra i sottolivelli di Zeeman è proporzionale al campo magnetico, questo effetto è sfruttato dagli astronomi per misurare il campo magnetico del Sole o di altre stelle.

Esiste inoltre anche il cosiddetto effetto Zeeman anomalo legato a transizioni in cui lo spin totale degli elettroni è diverso da zero. Questo fenomeno venne definito "anomalo" perché ai tempi in cui fu scoperto non si era ancora a conoscenza del concetto di spin elettronico, e quindi non fu possibile descriverlo in modo esauriente. Se la forza del campo magnetico è troppo elevata, l'effetto non diviene più lineare; a campi di forza ancora superiore, l'accoppiamento elettronico è disturbato e le linee spettrali subiscono un riordinamento. Questo fenomeno è noto come effetto Paschen-Back.

Elettrone in campo magnetico uniforme

L'hamiltoniano di un elettrone in un campo elettromagnetico è descritto per analogia al caso classico da:

$H={\frac {1}{2m}}\left(\mathbf {p} +{\frac {e}{c}}\mathbf {A} \right)^{2}-eV$

dove $\mathbf {A}$ è il potenziale vettore e $V$ è il potenziale scalare del campo elettromagnetico, come suggeriscono le equazioni di Maxwell. L'equazione di Schrödinger diventa:

$i\hbar {\frac {\partial \psi }{\partial t}}=H\psi =\left[-{\frac {\hbar ^{2}}{2m}}\left(\mathbf {\nabla } +{\frac {ie}{\hbar c}}\mathbf {A} \right)^{2}-eV\right]\psi$

Per il caso dell'effetto Zeemann poniamoci nel caso in cui il campo magnetico $\mathbf {B}$ esterno e uniforme, diretto secondo l'asse z:

$\mathbf {B} =B\mathbf {z}$

allora in base alla relazione $\mathbf {B} =\mathbf {\nabla } \times \mathbf {A}$ abbiamo:

$B={\frac {\partial A_{y}}{\partial x}}-{\frac {\partial A_{x}}{\partial y}}$

allora il potenziale vettore è scelto come:

$\mathbf {A} =(A_{x},A_{y},A_{z})=\left(-{\frac {By}{2}},{\frac {Bx}{2}},0\right)$

L'hamiltoniana diventa:

$H={\frac {1}{2m}}\left[\left(p_{x}-{\frac {e}{2c}}By\right)^{2}+\left(p_{y}+{\frac {e}{2c}}Bx\right)^{2}+p_{z}^{2}\right]-eV$

che riscritta nella forma:

$H=H_{0}+{\frac {e}{2mc}}BL_{z}+{\frac {e^{2}}{8mc^{2}}}B^{2}(x^{2}+y^{2})$

dove abbiamo chiamiato:

$H_{0}={\frac {1}{2m}}p^{2}-eV$

che rappresenta l'hamiltoniana imperturbata, dove m rappresenta la massa ridotta, dal momento che in genere si trattano le soluzioni senza approssimazioni sul moto dell'elettrone, e i termini aggiuntivi possono considerarsi perturbazioni su $H_{0}$. Possiamo quantificare l'ordine di grandezza sapendo che i valori medi di $\langle L_{z}\rangle \sim \hbar$ e di $\langle x^{2}+y^{2}\rangle \sim a_{0}^{2}$ dove $a_{0}$ è il raggio di Bohr:

${\frac {{\frac {e^{2}}{8mc^{2}}}a_{0}^{2}B^{2}}{{\frac {e}{2mc}}\hbar B}}\simeq {\frac {e^{2}}{4\hbar c}}{\frac {B}{e/a_{0}^{2}}}\simeq {\frac {B}{9\cdot 10^{9}}}\,{\mbox{ Gauss }}$

e

${\frac {{\frac {e}{2mc}}\hbar B}{(e^{2}/a_{0})}}\simeq {\frac {\frac {\hbar B}{mc}}{(2e/a_{0})}}\simeq {\frac {B}{5\cdot 10^{9}}}\,{\mbox{ Gauss }}$

che come si vede i due termini sono piccoli per i campi magnetici tipici ottenibili in laboratorio che sono di $B\simeq 10^{4}$ Gauss, cioè perturbazioni almeno dell'ordine $10^{-5}$.

Il contributo lineare in $B$ rappresenta il contributo paramagnetico e deriva dall'interazione magnetica tra il momento magnetico orbitale ${\vec {\mu }}$ e quello angolare:

$\mathbf {\mu } =-{\frac {e^{2}}{2mc}}\mathbf {L}$

con energia

$-\mathbf {\mu } \cdot \mathbf {B} =\omega _{L}L_{z}$

dove:

$\omega _{L}={\frac {e}{2mc}}B$

è la frequenza di Larmor. In pratica è come se l'elettrone, percorrendo l'orbita, fosse assimilabile a una piccola spira percorsa da una corrente elettrica, che in presenza di campo magnetico produce un momento magnetico: il momento angolare orbitale precede allora intorno all'asse z con una velocità angolare pari a $\omega _{L}$, e la quantità $e/2mc$ è detta rapporto giromagnetico. Il rapporto giromagnetico interviene nella definizione del magnetone di Bohr:

$\mu _{B}={\frac {e\hbar }{2mc}}=5.788\cdot 10^{-5}\,\,eV\,T^{-1}$

Il contributo quadratico in $\mathbf {B}$ rappresenta il contributo diamagnetico e deriva dal momento magnetico indotto da $\mathbf {B}$ che in genere è ancora più modesto energeticamente rispetto a quello paramagnetico.

I due contributi, in particolare il contributo lineare in $\mathbf {B}$, non modificano gli stati, ed ogni livello degenere si separa in $(2l+1)$ livelli equidistanziati di $\hbar \omega _{L}$: si tratta dell'effetto Zeeman normale. Si verifica inoltre che anche i livelli con $l=m=0$, che a priori non dovrebbero essere influenzati dal contributo paramagnetico, subiscono uno sdoppiamento a causa della presenza della degenerazione di spin: questo fenomeno è l'effetto Zeeman anomalo.

Effetto Zeeman normale

L'effetto Zeeman normale può essere descritto con l'aiuto di un modello semi-classico, considerando l'elettrone come una particella che descrive un'orbita attorno al nucleo atomico e che possiede un momento angolare quantizzato, come descritto dal modello atomico di Bohr.

Percorrendo l'elettrone un'orbita di raggio r con velocità v, si ottiene una corrente elettrica I data dalla relazione

$I=-e\cdot {\frac {v}{2\pi r}}$.

Questa corrente genera un campo magnetico dato da

$\mathbf {B} ={\frac {\mu _{0}}{4\pi }}{\frac {\mathbf {J} \times \mathbf {r} }{r^{3}}}=-{\frac {Ze\mu _{0}}{4\pi }}{\frac {\mathbf {v} \times \mathbf {r} }{r^{3}}}$

e un momento di dipolo magnetico:

$\mathbf {\mu _{l}} =I\cdot \mathbf {A} =-{\frac {evr}{2}}\cdot \mathbf {n} =-{\frac {e}{2m_{e}}}\cdot \mathbf {L}$

dove il vettore $\mathbf {A}$ è il vettore di superficie, ed è perpendicolare all'area dell'orbita descritta dall'elettrone, mentre il momento angolare è:

$\mathbf {L} =\mathbf {r} \times \mathbf {p} =m_{e}rv\cdot \mathbf {n}$.

L'espressione dell'energia di interazione magnetica, che rappresenta l'energia aggiunta dalla presenza del campo magnetico, diviene quindi:

$H_{magn}=-\mathbf {\mu _{l}} \cdot \mathbf {B} ={\frac {e}{2m_{e}}}\cdot \mathbf {L} \cdot \mathbf {B} ={\frac {e\hbar m_{l}}{2m_{e}}}B=\mu _{B}Bm_{l}$

dove $\mu _{B}$ è il magnetone di Bohr.
Tale espressione dipende esclusivamente da $m_{l}$, e l'effetto del campo è quello di rimuovere la sua degenerazione, cioè separare i 2l + 1 valori che esso può assumere.
Gli stati ad un dato livello energetico mantengono la degenerazione rispetto a $L^{2}$, mentre gli autostati di $L_{z}$ sono separati da una differenza di energia pari a

$\delta E_{M}=\mu _{B}B\$

proporzionale al campo applicato.

Effetto Zeeman anomalo

Nella descrizione dell'effetto Zeeman anomalo occorre considerare lo spin dell'elettrone. L'estensione della trattazione semi-classica in questo caso non è più possibile, essendo il fenomeno di natura puramente quantomeccanica.
Per definire il potenziale del campo magnetico si deve tenere conto dell'accoppiamento tra il momento magnetico angolare

$\mathbf {\mu _{L}} =-{\frac {\mu _{B}}{\hbar }}\mathbf {L}$

ed il momento magnetico di spin

$\mathbf {\mu _{S}} =-g_{s}{\frac {\mu _{B}}{\hbar }}\mathbf {S}$

che si descrive attraverso il momento magnetico totale

$\mathbf {\mu _{J}} =\mathbf {\mu _{S}} +\mathbf {\mu _{L}} =-{\frac {\mu _{B}}{\hbar }}\left(\mathbf {L} +g_{s}\mathbf {S} \right)$

dove il rapporto giromagnetico di spin è $g_{s}\approx 2$.

Da questa relazione è possibile notare come $\mathbf {\mu _{J}}$ e il momento angolare $\mathbf {J}$ non siano paralleli a causa dell'effetto del momento di spin anomalo.
Il termine di interazione con un campo magnetico esterno $\mathbf {B}$ è dunque:

$H_{magn}=-\mathbf {\mu _{J}} \mathbf {B}$

Essendo presente l'interazione spin-orbita $H_{s-o}$, lo spettro energetico è dato dalla diagonalizzazione dell'operatore di interazione totale $H_{magn}+H_{s-o}$. Dal momento che i due termini non sono diagonalizzabili simultaneamente, si studiano i due casi limite: il caso in cui l'interazione spin-orbita sia trascurabile, ottenendo l'effetto Paschen-Back, ed il caso in cui non sia trascurabile, ponendo che il campo magnetico sia sufficientemente debole da poter considerare $H_{magn}$ come una perturbazione all'hamiltoniana di spin-orbita, ottenendo il limite di Zeeman.

Limite di Paschen-Back

Nel caso in cui il campo magnetico sia di intensità tale da poter trascurare l'interazione spin-orbita l'operatore $H_{magn}$ è diagonale nella base $|l,s,m_{l},m_{s}\rangle$, in cui i vettori $\mathbf {L}$ e $\mathbf {S}$ sono disaccoppiati. In questo limite è quindi possibile ignorare l'influenza dello spin, e ci si riconduce all'effetto Zeeman normale.
La quantizzazione del momento angolare, ponendo che il campo sia diretto verso l'asse z, permette di ricavare:

$E_{magn}\simeq \langle m_{l},m_{s}|H_{magn}|m_{l},m_{s}\rangle =-\mathbf {\mu _{J}} \mathbf {B} ={\frac {\mu _{B}}{\hbar }}\left(\mathbf {L} +2\mathbf {S} \right)\mathbf {B} =\mu _{B}B(m_{l}+2m_{s})$

Il numero quantico magnetico è ora $m=m_{l}+2m_{s}$, ed livelli energetici sono quindi

$E=E_{0}+\mu _{B}mB\$

La separazione delle linee è funzione solamente della degenerazione numero quantico magnetico, che viene rimossa dal campo magnetico esterno.

Limite di Zeeman

Nel caso in cui l'interazione spin-orbita non possa essere trascurata $H_{magn}$ agisce come perturbazione all'interazione $H_{s-o}$. Dal momento che l'operatore $H_{s-o}$ è diagonale nella base $|j,m_{j},l,s\rangle$, in cui i vettori $\mathbf {L}$ e $\mathbf {S}$ sono accoppiati, $\mathbf {\mu _{J}}$ e $\mathbf {J}$ non sono paralleli, e la componente del primo sul secondo è data da

$\mu _{J}=-{\frac {\mu _{B}}{2\hbar J}}(3J^{2}+S^{2}-L^{2})$

sapendo che $J_{z}=Jcos\theta$ si ottiene che la componente lungo l'asse z è

$\mu _{z}=J_{z}{\frac {\mu _{j}}{J}}$

Combinando le due precedenti espressioni si ottiene il valore medio:

$\langle \mu _{z}\rangle =-g_{j}\mu _{B}{\frac {\langle J_{z}\rangle }{\hbar }}$

dove $g_{j}$ è il fattore g di Landé relativo al momento angolare totale, ricavabile dalla relazione

$g_{J}=1+{\frac {J(J+1)+S(S+1)-L(L+1)}{2J(J+1)}}$

Lo spostamento dei livelli energetici è dato dalla correzione generata dal termine perturbativo $H_{magn}$:

$E_{magn}\simeq \langle j,m_{j}|H_{magn}|j,m_{j}\rangle =-\langle \mu _{z}\rangle B=g\mu _{B}B{\frac {\langle J_{z}\rangle }{\hbar }}$

essendo che

$\langle J_{z}\rangle =\hbar m_{j}$

si ottiene in definitiva

$E_{magn}\simeq g_{j}\mu _{B}Bm_{j}$

Tale espressione rappresenta lo spostamento dei livelli energetici a causa dell'applicazione del campo magnetico: le energie dei singoli livelli differiscono a causa del diverso $m_{j}$ di ognuna. La differenza di energia differisce inoltre in funzione di $L_{j}$ a causa della variazione del fattore g in funzione di l e j. Questo contributo deve essere sommato al termine di spin-orbita per ricavare i livelli energetici del sistema.
Per atomi a più elettroni il fattore g di Landé, nel caso di atomi leggeri in cui valga l'accoppiamento di Russell-Saunders, è ottenuto semplicemente sostituendo ai momenti angolari j, m e l i rispettivi momenti totali J, M e L. Dal momento che l'interazione spin orbita cresce come Z⁴, il limite di Zeeman è il caso più comune.

Effetto Zeeman quadratico

Un campo magnetico esterno è sempre in grado di generare un momento indotto anche nel caso in cui non si abbia un momento magnetico permanente. Come noto, il valore del momento indotto risulta essere uguale a

${\vec {\mu }}_{ind}=\alpha _{m}{\vec {B}}$.

Questa interazione produce un'ulteriore suddivisione dell'energia calcolabile dall'equazione

$\Delta E=\alpha _{m}\cdot B^{2}$.

Questo effetto viene generalmente trascurato rispetto all'effetto Zeeman lineare.

L'Effetto Zeeman applicato all'assorbimento atomico

Nell'ambito della spettroscopia, l'Effetto Zeeman trova un'applicazione significativa nell'analisi dell'assorbimento atomico.

L'assorbimento atomico è il fenomeno mediante il quale gli atomi assorbono energia elettromagnetica, tipicamente nella forma di luce. L'introduzione di un campo magnetico modifica la struttura delle linee spettrali, producendo più linee distinte rispetto al caso senza campo magnetico. Questo fenomeno consente agli scienziati di ottenere informazioni più dettagliate sulla distribuzione degli elettroni negli atomi, contribuendo così a una comprensione più approfondita delle proprietà atomiche.

L'analisi dell'Effetto Zeeman nell'ambito dell'assorbimento atomico fornisce una metodologia precisa per studiare la struttura fine degli spettri atomici, rendendo possibile l'indagine di fenomeni specifici legati all'interazione tra campi magnetici e gli orbitali elettronici degli atomi. Questa applicazione pratica dell'Effetto Zeeman gioca un ruolo fondamentale nelle ricerche scientifiche volte a esplorare e comprendere le proprietà degli atomi in dettaglio.

Un'applicazione significativa dell'Effetto Zeeman si manifesta nella correzione dell'assorbimento di fondo nella spettrometria ad assorbimento atomico. In questa tecnica, la luce emessa dalla lampada viene assorbita dall'analita in forma atomica e, eventualmente, da altre molecole o frammenti presenti nella matrice complessa del campione. Per distinguere tali contributi, si sfrutta l'Effetto Zeeman.

In assenza di campo magnetico, l'analita assorbe a una specifica lunghezza d'onda $\nu _{0}$, indipendentemente dalla polarizzazione del fascio. Introducendo un campo magnetico, si verifica lo splitting dei livelli energetici, consentendo l'assorbimento solo se il fascio è polarizzato parallelamente al campo magnetico $B$.

Un filtro polarizzatore ortogonale a $B$ impedisce l'assorbimento dell'analita a $\nu _{0}$, consentendo teoricamente l'assorbimento a frequenze maggiori o minori di $\nu _{0}$. Tuttavia, dato che il range di frequenze emesso dalla lampada per l'assorbimento atomico è ristretto attorno a $\nu _{0}$, in pratica tali transizioni non si verificano.

Applicando un campo magnetico e un polarizzatore ortogonale, si permette l'assorbimento del fondo e dell'analita a campo spento, mentre a campo acceso si impedisce l'assorbimento dell'analita. L'assorbimento netto dell'analita si calcola per differenza.

Il sistema può utilizzare un campo magnetico pulsato o un polarizzatore rotante tra la sorgente e l'analita. Analogamente, è possibile applicare l'Effetto Zeeman alla sorgente (lampada HCL), splittando e polarizzando la lunghezza d'onda emessa. La selezione del fascio centrale o laterale avviene tramite un polarizzatore rotante, consentendo la correzione dell'assorbimento dell'analita e del fondo nella spettrometria ad assorbimento atomico.

Bibliografia

• P. Zeeman, On the influence of Magnetism on the Nature of the Light emitted by a Substance, Phil. Mag. 43: 226 (1897).
• P. Zeeman, Doubles and triplets in the spectrum produced by external magnetic forces, Phil. Mag. 44: 55 (1897).
• P. Zeeman, The Effect of Magnetisation on the Nature of Light Emitted by a Substance.
• P. Forman, Alfred Landé and the anomalous Zeeman Effect, 1919-1921, Historical Studies in the Physical Sciences 2: 153-261 (1970).
• B. Welz, M. Sperling, Atomic Absorption Spectrometry, third edition, Wiley-VHC, 1999.

Altri progetti

Altri progetti

• Wikimedia Commons

• Wikimedia Commons contiene immagini o altri file su effetto Zeeman

Collegamenti esterni

• Proprietà magnetiche degli atomi (PPT), su cdm.unimo.it. URL consultato il 16 luglio 2007 (archiviato dall'url originale il 27 novembre 2009).
• Animazione sui momenti cinetici orbitali e di spin. In Inglese. Università Paris Saclay