e (costante matematica)

e (Numero di Eulero)
Simbolo	e
Valore	2,71828 18284 59045 23536 ... (sequenza A001113 dell'OEIS)
Origine del nome	Eulero
Frazione continua	[2; 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, ...] (sequenza A003417 dell'OEIS)
Insieme	numeri trascendenti
Costanti correlate	Costante di Gelfond, Costante Omega
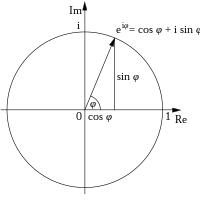La costante e compare nella formula di Eulero, una delle identità matematiche più importanti.

In matematica, e è una costante che, insieme a pi greco, è tra le più importanti per via delle sue numerose applicazioni, in modo particolare nell'ambito dell'analisi matematica.

Poiché è un irrazionale (e, in particolare, trascendente), non è esprimibile come frazione o come numero decimale periodico: la sua approssimazione con 55 cifre decimali è

2,71828 18284 59045 23536 02874 71352 66249 77572 47093 69995 95749...

Essa viene chiamata in ambito internazionale numero di Eulero, in Italia talvolta numero di Nepero.

Il numero di Eulero è collegato con la funzione esponenziale che associa ad un numero reale $x$ il numero dato dalla potenza $e^x$, e con la funzione logaritmo naturale (la funzione inversa dell'esponenziale). In particolare in maniera formale è possibile definire $e$ come il valore che la funzione esponenziale $e^x$ assume in $x = 1$.

Definizioni

Il numero e può essere definito in uno dei seguenti modi equivalenti:

• come il valore del limite

$e := \lim_{n\to\infty} {\left(1+\frac{1}{n}\right)}^n$;

• come la somma della serie

$e := \sum_{n=0}^\infty {1 \over n!} = {1 \over 0!} + {1 \over 1!} + {1 \over 2!} + {1 \over 3!} + {1 \over 4!} + \cdots$

(Qui n! sta per il fattoriale di n. Proprio per ottenere, per lo sviluppo in serie della funzione esponenziale, la scrittura compatta $e^x= \sum_{n=0}^\infty {x^n \over n!}$ , si pone per definizione 0!=1).

Una dimostrazione dell'equivalenza di queste definizioni è data qui sotto. Entrambe le definizioni sono usate in modo analogo nella definizione della funzione esponenziale.

Un modo alternativo (non standard) di definire e coinvolge le equazioni differenziali: il numero di Eulero si può definire come il valore in $x=1$ della funzione $f(x)$ soluzione unica del problema di Cauchy dato dall'equazione differenziale $f^\prime(x)=f(x)$ con condizioni iniziali $f(0)=1$.

Proprietà

Numero irrazionale e trascendente

Per approfondire, vedi dimostrazione della irrazionalità di e e dimostrazione della trascendenza di e.

Il numero e è irrazionale e più precisamente un numero trascendente, cioè un numero reale costruibile non algebrico. Questo è stato il primo numero che si è dimostrato essere trascendente senza essere stato costruito specificamente per essere collocato nell'insieme dei numeri reali non algebrici (come era accaduto in precedenza per la costante di Liouville). Una dimostrazione della irrazionalità di e è stata data da Charles Hermite nel 1873. Si presume inoltre che esso sia un numero normale.

Formula di Eulero

La costante e compare nella formula di Eulero, una delle più importanti identità della matematica:

$e^{ix} = \cos(x) + i\,\mathrm{sen}(x),$

dove $i$ indica l'unità immaginaria. Il caso particolare con x = π è noto come identità di Eulero:

$e^{i\pi}+1=0;$

questa uguaglianza è stata chiamata da Richard Feynman "gioiello di Eulero".

Frazione continua

Lo sviluppo di e come frazione continua infinita è espresso dalla seguente interessante configurazione:

$e - 1 = [1; 0, 1, 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, \ldots]$

Proprietà analitiche

Il numero e è il punto centrale della commutazione dell'elevamento a potenza. Siano date tutte le coppie (x,y) per le quali x^y=y^x. Oltre al caso banale x=y, l'unica coppia intera (e razionale) per cui vale la proprietà è formata dai numeri 2 e 4, ma vale anche per infinite coppie irrazionali distribuite lungo una curva nel primo quadrante, asintotica alle rette x=1 e y=1. Tale curva e la retta y=x si intersecano nel punto (e, e). Sempre in merito a funzioni esponenziali, la radice x-esima di x, ovvero x^1/x, ha massimo per x=e e l'esponenziale x-esimo di x, ovvero x^x, ha minimo per x=1/e.

Storia

Nel corso degli anni il numero e è stato approssimato con una precisione di milioni di cifre decimali.

Il primo riferimento alla costante e in letteratura risale al 1618 ed è contenuto nella tavola di un'appendice di un lavoro sui logaritmi da John Napier. Tuttavia nella tavola non appare direttamente la costante, ma solo un elenco di logaritmi naturali calcolabili a partire dalla costante. Si presume che la tavola fosse stata scritta da William Oughtred. La prima espressione di e come una costante è stata trovata da Jakob Bernoulli:

$\lim_{n\to\infty} \left(1+\frac{1}{n}\right)^n$

Da questa espressione, però, risulta difficile ricavare un buon valore numerico per la costante.

La prima citazione della costante, rappresentata dalla lettera b compare in due lettere di Gottfried Leibniz a Christiaan Huygens nel 1690 e 1691. Leonhard Euler ha iniziato ad usare la lettera e per la costante nel 1727, e il primo uso di e in una pubblicazione compare nella Mechanica di Eulero (1736). Mentre negli anni seguenti alcuni ricercatori hanno usato la lettera c, l'uso di e si è fatto più comune ed oggi è usato come simbolo tipico per la costante.

Si sostiene anche che e sia stata usata sia dai greci antichi che dagli egizi, rispettivamente per la costruzione del Partenone e della grande piramide, in quanto in queste costruzioni si trovano lunghezze tipiche che hanno come rapporto il suo valore. I greci antichi usavano per questa costante l'appellativo Αρμονικός σταθερά o costante armonica, la denotavano con la lettera ε e usavano per essa il valore 2.72.

Le esatte motivazioni per la scelta della lettera e non sono note, ma si può supporre che sia dovuta al fatto che la lettera e è l'iniziale della parola esponenziale. Un'altra motivazione sta nel fatto che le lettere a, b, c, e d venivano già frequentemente usate per altri oggetti matematici ed e era la prima lettera dell'alfabeto latino non utilizzata. È improbabile che Eulero abbia scelto la lettera in quanto sua iniziale, poiché il numero non era una sua scoperta, ma era già ampiamente noto ai matematici dell'epoca.

Dimostrazione dell'equivalenza delle due formulazioni

La seguente dimostrazione prova l'equivalenza dello sviluppo in serie infinita presentato in precedenza e l'espressione del limite studiata da Bernoulli.

Definiamo

$s_n := \sum_{k=0}^n\frac{1}{k!}~,$

$t_n=\left(1+\frac{1}{n}\right)^n ~.$

Dal teorema binomiale,

$t_n=\sum_{k=0}^n{n \choose k}\frac{1}{n^k}=1+1+\sum_{k=2}^n\frac{n(n-1)(n-2)\cdots(n-(k-1))}{k!\,n^k}$

$=1+1+\frac{1}{2!}\left(1-\frac{1}{n}\right)+\frac{1}{3!}\left(1-\frac{1}{n}\right)\left(1-\frac{2}{n}\right)+\cdots+\frac{1}{n!}\left(1-\frac{1}{n}\right)\cdots\left(1-\frac{n-1}{n}\right)\le s_n$

tale che

$\limsup_{n\to\infty}t_n \le \limsup_{n\to\infty}s_n = e ~.$

Qui deve essere usato il limite superiore o limsup, poiché non è ancora noto che t_n converge effettivamente. Ora, per l'altra direzione, si nota che dall'espressione sopra di t_n, se 2 ≤ m ≤ n, abbiamo

$1+1+\frac{1}{2!}\left(1-\frac{1}{n}\right)+\cdots+\frac{1}{m!}\left(1-\frac{1}{n}\right)\left(1-\frac{2}{n}\right)\cdots\left(1-\frac{m-1}{n}\right)\le t_n$

Fissato m si fa tendere n all'infinito. Otteniamo

$s_m = 1+1+\frac{1}{2!}+\cdots+\frac{1}{m!} \le \liminf_{n\to\infty}t_n$

(di nuovo, dobbiamo usare il limite inferiore o liminf poiché non è ancora garantito che t_n converge). Ora, considerando la disuguaglianza precedente, m si avvicina all'infinito, e la colloca assieme all'altra disuguaglianza. Questa diventa

$\limsup_{n\to\infty}t_n \le e \le \liminf_{n\to\infty}t_n \le \limsup_{n\to\infty}t_n$

Questo completa la dimostrazione.

Rappresentazione stocastica

Oltre alle rappresentazioni analitiche esatte per rappresentare $e$, esistono metodi stocastici per stimarlo. Una di queste parte da una sequenza infinita di variabili casuali indipendenti $X_1, X_2,...,$ distribuite uniformemente nell'intervallo $[0,1]$. Definito $V$ come il numero $n$ minimo tale che la somma dei primi n termini sia maggiore di 1

$V = \min \left \{n | X_1+X_2+...+X_n>1 \right \}$

allora il valore atteso di V è $e$.

Bibliografia

• Eli Maor: e: The Story of a Number, ISBN 0-691-05854-7

Altri progetti

• Commons

• Commons contiene immagini o altri file su e (costante matematica)

Collegamenti esterni

• (EN) The number e (history)
• Il primo milione e i primi due milioni di cifre decimali del numero e

Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica