Rotore (matematica)

Nel calcolo differenziale vettoriale, il rotore di un campo vettoriale tridimensionale è un operatore differenziale che ad un campo vettoriale tridimensionale $\mathbf {A}$ fa corrispondere un altro campo vettoriale solitamente denotato da $\nabla \times \mathbf {A}$, dove $\nabla$ è l'operatore nabla, $\times$ è il prodotto vettoriale e $\nabla \times$ è l'operatore rotore. In termini intuitivi, esso esprime una rotazione infinitesima (ad esempio una velocità di rotazione) del vettore dato, associando a ogni punto dello spazio un vettore.

Si tratta di un vettore allineato con l'asse di rotazione; il suo verso è coerente con quello della rotazione secondo la regola della mano destra e la sua lunghezza è il valore della circuitazione del campo (la sua integrazione lungo un percorso chiuso) per unità di area, cioè nel limite in cui la curva di integrazione si riduce ad un punto.

Ad esempio, se come campo vettoriale si considera la velocità delle particelle che compongono un qualche fluido, il rotore del campo vettoriale è la densità di circolazione del fluido. I campi vettoriali che hanno rotore uguale a zero sul proprio dominio sono chiamati irrotazionali.

Il rotore misura la massima componente rotazionale piana nello sviluppo di Taylor di un campo vettoriale al primo ordine, ovvero nella linearizzazione del campo in 3 dimensioni. Pertanto, si tratta di un tipo di derivazione di un campo vettoriale. La relativa integrazione avviene tramite il teorema del rotore, caso particolare del teorema di Stokes, che mette in relazione l'integrale di superficie $S$ del rotore del campo vettoriale con l'integrale di linea del campo vettoriale lungo la frontiera $\partial S$ di $S$.

A differenza di gradiente e divergenza, generalizzare il rotore a spazi a più di tre dimensioni non è possibile. Esistono alcune generalizzazioni, ma solo in spazi tridimensionali (anche non euclidei come le varietà riemanniane tridimensionali) la definizione geometrica di rotore di un campo vettoriale fornisce un altro campo vettoriale. Da questo punto di vista, il rotore ha proprietà simili a quelle del prodotto vettoriale.

Interpretazione intuitiva

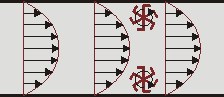
Supponiamo che un campo vettoriale (tridimensionale) $\mathbf {F}$ descriva la velocità di un fluido (non perfetto). Immaginando di fissare il centro di una piccola sfera in un punto, se questa sferetta ha una superficie ruvida allora incomincerà a ruotare su sé stessa, mossa dallo scorrere del fluido. Il rotore $\nabla \times \mathbf {F}$ valutato nel centro della sfera è un vettore che ha come direzione l'asse di rotazione della sfera e come lunghezza la metà del valore assoluto del momento angolare della sfera. Inoltre, il senso di rotazione è associato al vettore in accordo con la regola della mano destra.

Definizione

Sotto l'ipotesi che un campo vettoriale $\mathbf {F}$ sia di classe $C^{1}$, il rotore $\nabla \times \mathbf {F}$ di $\mathbf {F}$ è definito in ogni punto attraverso la sua proiezione su un versore $\mathbf {\hat {n}}$ di $\mathbb {R} ^{3}$ posto nel punto: si tratta del valore dell'integrale di linea $\oint _{C}\mathbf {F} \cdot d\mathbf {r}$ del campo in un piano ortogonale a $\mathbf {\hat {n}}$ nel limite in cui la curva $C$ di integrazione si riduca a un punto, cioè nel limite in cui l'area $A$ delimitata da $C$ tenda ad annullarsi, diviso per l'area $|A|$:

$(\nabla \times \mathbf {F} )\cdot \mathbf {\hat {n}} \ {\overset {\underset {\mathrm {def} }{}}{=}}\lim _{A\to 0}\left({\frac {1}{|A|}}\oint _{C}\mathbf {F} \cdot d\mathbf {r} \right).$

Si tratta di una scrittura del teorema del rotore, e si può interpretare il prodotto scalare tra $\nabla \times \mathbf {F}$ e il vettore unitario $\mathbf {n}$ come densità superficiale di circuitazione del campo $\mathbf {F}$ attorno alla direzione $\mathbf {\hat {n}}$.

Poiché $\mathbb {R} ^{3}$ è uno spazio con metrica euclidea, in un sistema di coordinate curvilinee ortogonali $(u_{1},u_{2},u_{3})$, come per esempio le stesse coordinate cartesiane, sferiche, cilindriche, ellittiche o paraboliche, la terza componente del rotore di $\mathbf {F} =(F_{1},F_{2},F_{3})$ è data da:

$(\nabla \times \mathbf {F} )\,_{3}={\frac {1}{h_{1}h_{2}}}\left({\frac {\partial (h_{2}F_{2})}{\partial u_{1}}}-{\frac {\partial (h_{1}F_{1})}{\partial u_{2}}}\right).$

Le restanti due componenti del rotore (la prima e la seconda, nell'ordine) si ottengono dalla permutazione ciclica degli indici: 3,1,2 → 1,2,3 → 2,3,1.

Se, ad esempio, le $(x_{1},x_{2},x_{3})$ sono coordinate cartesiane e le $(u_{1},u_{2},u_{3})$ sono coordinate curvilinee ortogonali, si ha:

$h_{i}={\sqrt {\sum \limits _{j=1}^{3}\left({\frac {\partial x_{j}}{\partial u_{i}}}\right)^{2}}}.$

In un sistema di coordinate curvilinee generale, $(u^{k})$, il rotore è dato da:

$(\nabla \times \mathbf {F} )^{k}=e^{k\ell m}\nabla _{\ell }F_{m}\,,$

dove si è usata la notazione di Einstein e $e^{k\ell m}$ denota il tensore Levi-Civita (che è il simbolo di Levi-Civita moltiplicato per la radice quadrata della metrica euclidea espressa in coordinate curvilinee qualsiasi) e $\nabla _{\ell }$ denota la derivata covariante. Equivalentemente,

$(\nabla \times \mathbf {F} )=\mathbf {e} _{k}e^{k\ell m}\nabla _{l}F_{m}\,,$

dove $\mathbf {e} _{k}$ sono i campi vettoriali coordinati, associati al sistema di coordinate curvilinee generale, ovvero $\mathbf {e} _{k}={\partial \over {\partial u^{k}}}$.

Utilizzando invece la derivata esterna:

$\nabla \times \mathbf {F} =\left[\star \left({\mathbf {d} }F^{\flat }\right)\right]^{\sharp },$

dove $\flat$ e $\sharp$ sono isomorfismi musicali e $\star$ è il duale di Hodge.

Quest'ultima formulazione è valida in un sistema di coordinate generico, e consente di estendere il rotore a varietà riemanniane tridimensionali orientate. Dato che dipende dall'orientazione della varietà, il rotore è un operatore chirale: se cambia l'orientazione cambia anche il verso del rotore.

Coordinate cartesiane

In coordinate cartesiane, detti $\mathbf {i}$, $\mathbf {j}$, e $\mathbf {k}$ i versori degli assi, il rotore di un campo vettoriale $\mathbf {F} =(F_{x},F_{y},F_{z})$ è il campo vettoriale $\nabla \times \mathbf {F}$ definito da:

$\nabla \times \mathbf {F} ={\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\\\{\frac {\partial }{\partial x}}&{\frac {\partial }{\partial y}}&{\frac {\partial }{\partial z}}\\\\F_{x}&F_{y}&F_{z}\end{vmatrix}}={\begin{vmatrix}0&{-{\frac {\partial }{\partial z}}}&{\frac {\partial }{\partial y}}\\\\{\frac {\partial }{\partial z}}&0&{-{\frac {\partial }{\partial x}}}\\\\{-{\frac {\partial }{\partial y}}}&{\frac {\partial }{\partial x}}&0\end{vmatrix}}\mathbf {F} ,$

dove nella seconda uguaglianza si è esplicitata l'equazione matriciale, mentre nella prima la scrittura indica il determinante formale della matrice; riallacciandosi alle espressioni valide in uno spazio euclideo richiamate più sopra, si ottiene il caso più semplice (quello con: $a_{i}=1$):

$\nabla \times \mathbf {F} =\mathbf {i} \left({\frac {\partial F_{z}}{\partial y}}-{\frac {\partial F_{y}}{\partial z}}\right)+\mathbf {j} \left({\frac {\partial F_{x}}{\partial z}}-{\frac {\partial F_{z}}{\partial x}}\right)+\mathbf {k} \left({\frac {\partial F_{y}}{\partial x}}-{\frac {\partial F_{x}}{\partial y}}\right).$

Coordinate cilindriche

Se si prende invece, nello spazio euclideo, un sistema di riferimento in coordinate cilindriche $(x=\rho \cos \phi ,y=\rho \sin \phi ,z=z)$, il rotore di $\mathbf {F} (\rho ,\phi ,z)=\mathbf {e} _{\rho }\ F_{\rho }+\mathbf {e} _{\phi }\ F_{\phi }+\mathbf {e} _{z}\ F_{z}$ è dato da:

$\nabla \times \mathbf {F} =\mathbf {e} _{\rho }\ \left({\frac {1}{\rho }}{\frac {\partial F_{z}}{\partial \phi }}-{\frac {\partial F_{\phi }}{\partial z}}\right)+\mathbf {e} _{\phi }\ \left({\frac {\partial F_{\rho }}{\partial z}}-{\frac {\partial F_{z}}{\partial \rho }}\right)+\mathbf {e} _{z}\ {\frac {1}{\rho }}\left({\frac {\partial (\rho F_{\phi })}{\partial \rho }}-{\frac {\partial F_{\rho }}{\partial \phi }}\right).$

Rotore come derivata esterna

A un campo vettoriale $\mathbf {F} =(F_{x},F_{y},F_{z})$ nello spazio possiamo associare una corrispondente 1-forma differenziale

$\omega =F_{x}\mathrm {d} x+F_{y}\mathrm {d} y+F_{z}\mathrm {d} z,$

allora la sua derivata esterna risulta essere la 2-forma

$\mathrm {d} \omega =\left({\frac {\partial F_{z}}{\partial y}}-{\frac {\partial F_{y}}{\partial z}}\right)dy\wedge dz+\left({\frac {\partial F_{x}}{\partial z}}-{\frac {\partial F_{z}}{\partial x}}\right)dz\wedge dx+\left({\frac {\partial F_{y}}{\partial x}}-{\frac {\partial F_{x}}{\partial y}}\right)dx\wedge dy$

$=(\nabla \times \mathbf {F} )_{x}dy\wedge dz+(\nabla \times \mathbf {F} )_{y}dz\wedge dx+(\nabla \times \mathbf {F} )_{z}dx\wedge dy.$

Identità vettoriali

Di seguito i campi vettoriali e scalari coinvolti saranno di classe $C^{2}$.

In coordinate cartesiane si mostra che $\nabla \times (\mathbf {v\times \mathbf {F} } )$ è uguale a:

$\nabla \times \left(\mathbf {v\times F} \right)=\left[\left(\mathbf {\nabla \cdot F} \right)+\mathbf {F\cdot \nabla } \right]\mathbf {v} -\left[\left(\mathbf {\nabla \cdot v} \right)+\mathbf {v\cdot \nabla } \right]\mathbf {F}$

e se si invertono il campo vettoriale e $\nabla$:

$\mathbf {v\ \times } \left(\mathbf {\nabla \times F} \right)=\nabla _{F}\left(\mathbf {v\cdot F} \right)-\left(\mathbf {v\cdot \nabla } \right)\mathbf {F}$

dove $\nabla _{F}$ significa che il gradiente agisce solo su $\mathbf {F}$.

Sempre in coordinate cartesiane, $\nabla \times (\nabla \times \mathbf {F} )$ è dato da:

$\nabla \times \left(\mathbf {\nabla \times F} \right)=\mathbf {\nabla } (\mathbf {\nabla \cdot F} )-\nabla ^{2}\mathbf {F}$

dove $\nabla ^{2}\mathbf {F}$ è il laplaciano vettoriale di $\mathbf {F}$. Questa relazione può essere vista come un caso particolare della precedente sostituendo v → ∇.

Il rotore del gradiente di un campo scalare $\phi$ è nullo:

$\nabla \times (\nabla \phi )={\vec {0}}$, nel qual caso se il campo scalare $\phi$, come anche il campo vettoriale irrotazionale $\nabla \phi$, sono definiti in un insieme semplicemente connesso come definito dal lemma di Poincaré, allora $\phi$ è il potenziale scalare del campo vettoriale conservativo $-\nabla \phi$.

mentre se $\varphi$ è una funzione scalare e $\mathbf {F}$ un campo vettoriale:

$\nabla \times (\varphi \mathbf {F} )=\nabla \varphi \times \mathbf {F} +\varphi \nabla \times \mathbf {F} .$

Esempio

Si consideri il seguente campo vettoriale, che è tangente alle circonferenze concentriche all'asse $z$ e la cui intensità aumenta linearmente con la distanza da esso; in coordinate cartesiane:

$\mathbf {F} (x,y,z)=y{\boldsymbol {\hat {x}}}-x{\boldsymbol {\hat {y}}}.$

mentre in coordinate cilindriche (più comode in questo caso viste le simmetrie del campo):

$\mathbf {F} (\rho ,\phi ,z)=-{\rho }\mathbf {e} _{\phi }$

Una sua rappresentazione nel piano cartesiano (a meno di un fattore di riduzione di scala) è:

Da una semplice ispezione visiva si può solo notare che il campo "sta ruotando" e che la sua intensità aumenta con la distanza dall'asse; ci si può aspettare che esso sia capace, localmente, di fare ruotare una pallina posta in ogni suo punto, secondo la regola della mano destra (il verso del rotore è entrante nella pagina: usando un sistema di coordinate cartesiane standard, ciò corrisponde alla direzione delle z negative). La prova analitica viene calcolando il rotore; in coordinate cartesiane:

$\mathbf {\nabla } \times \mathbf {F} =0{\boldsymbol {\hat {x}}}+0{\boldsymbol {\hat {y}}}+\left[{\frac {\partial }{\partial x}}(-x)-{\frac {\partial }{\partial y}}y\right]{\boldsymbol {\hat {z}}}=-2{\boldsymbol {\hat {z}}}.$

mentre in coordinate cilindriche:

$\mathbf {\nabla } \times \mathbf {F} =\mathbf {e} _{z}\ {\frac {1}{\rho }}\left({\frac {\partial (\rho F_{\phi })}{\partial \rho }}\right)=-2\mathbf {e} _{z}\ .$

In questo caso il rotore è uguale in tutto lo spazio, indipendentemente dal punto che si considera, e quindi l'entità della rotazione nel campo vettoriale considerato è la stessa ovunque. La sua semplice rappresentazione nello spazio cartesiano è pertanto:

Bibliografia

• (EN) Arfken, George B. and Hans J. Weber. Mathematical Methods For Physicists, Academic Press; 6 edition (June 21, 2005). ISBN 978-0-12-059876-2.
• (EN) Korn, Granino Arthur and Theresa M. Korn, Mathematical Handbook for Scientists and Engineers: Definitions, Theorems, and Formulas for Reference and Review, New York, Dover Publications, pp. 157–160, ISBN 0-486-41147-8.
• (EN) Kaplan, W. "The Curl of a Vector Field." §3.5 in Advanced Calculus, 4th ed. Reading, MA: Addison-Wesley, pp. 186–187, 1991.
• (EN) Morse, P. M. and Feshbach, H. "Curl." In Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 39–42, 1953.
• (EN) Schey, H. M. Div, Grad, Curl, and All That: An Informal Text on Vector Calculus, 3rd ed. New York: W. W. Norton, 1997.

Voci correlate

• Gradiente
• Divergenza
• Teorema del rotore
• Teorema di Helmholtz
• Teorema di Stokes

Collegamenti esterni

• (EN) curl, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
• (EN) Eric W. Weisstein, Rotore, su MathWorld, Wolfram Research.
• (EN) Rotore, su Encyclopaedia of Mathematics, Springer e European Mathematical Society.

Controllo di autorità	GND (DE) 4178485-6