Molecola biatomica

Una molecola biatomica è una molecola formata da due atomi; esse costituiscono pertanto le più semplici forme di composti molecolari esistenti. Le molecole biatomiche si distinguono in molecole omonucleari, composte da atomi dello stesso elemento chimico, ed eteronucleari, composte da atomi di elementi diversi.
Molecole omonucleari[modifica | modifica wikitesto]
Una molecola biatomica omonucleare è una molecola formata da due atomi uguali.
Alcuni elementi della tavola periodica possiedono uno stato standard sotto forma di molecola biatomica, come nel caso dell'idrogeno (H2), azoto (N2), ossigeno (O2), fluoro (F2), cloro (Cl2), bromo (Br2) e iodio (I2). Non sono Biatomici il Fosforo (P4 ), e lo Zolfo (S8)
La molecola H2+[modifica | modifica wikitesto]


Le molecole diatomiche omonucleari sono composte da due atomi dello stesso elemento chimico; la più semplice di queste è H2+, per la quale l'equazione elettronica assume la forma:[1]
dove , il secondo e il terzo termine rappresentano l'attrazione Vne dell'elettrone nei confronti dei nuclei e il quarto la repulsione dei due nuclei.
I due protoni formano due buche di potenziale, e la funzione d'onda dell'elettrone è la combinazione lineare di due funzioni d'onda idrogenoidi :[2]
La funzione d'onda costituisce l'orbitale molecolare di legame, la funzione costituisce l'orbitale di antilegame.[3] L'orbitale di legame ha energia minore dell'orbitale di antilegame, ed è per questo il più probabile.
Le funzioni , sebbene descrivano bene la distribuzione di probabilità dell'elettrone nello stato fondamentale, non sono soluzioni esatte dell'equazione elettronica.
La funzione d'onda , nello spazio tra i due nuclei, è maggiore delle singole funzioni d'onda idrogenoidi , ed è questo fatto che genera il legame covalente tra i due nuclei. Si nota infatti che la densità di probabilità associata alla funzione d'onda:
contiene un termine di interazione, il doppio prodotto, che rappresenta la sovrapposizione delle due funzioni d'onda: si tratta di una regione di carica negativa che unisce i due nuclei di carica opposta.
Per quanto riguarda l'orbitale di antilegame , esso si annulla a metà tra i due nuclei, dove genera una densità di probabilità minore di quella che avrebbe senza il termine di sovrapposizione.
La molecola H2[modifica | modifica wikitesto]


Si consideri ora la molecola H2, la più semplice molecola neutra. Avendo due elettroni, la funzione d'onda elettronica di singoletto è data da:[4]
e rappresenta l'orbitale di legame, mentre quella di tripletto da:[5]
che rappresenta l'orbitale di antilegame, dove:
e
sono gli stati di spin, in cui + rappresenta lo spin-up, - lo spin-down.
La densità di probabilità spaziale è:[5]
Anche in questo caso il termine di interferenza rappresenta la sovrapposizione delle funzioni d'onda idrogenoidi nella regione tra i nuclei, e comporta un aumento di carica nel caso di singoletto (segno +), e una diminuzione di carica nel tripletto (segno -).
Molecole biatomiche omonucleari del primo e secondo periodo[modifica | modifica wikitesto]
Le molecole biatomiche omonucleari del primo e secondo periodo (H-Ne) sono state ampiamente studiate.
Sono tutte molecole diamagnetiche (S=0), eccetto B2 e O2 che sono paramagnetiche (S=1). nella tabella che segue sono riportati per ogni molecola il termine di stato fondamentale, il valore dell'energia di dissociazione (De) e della distanza di equilibrio (Re).
Gli orbitali molecolari che vengono riempiti in successione sono ottenuti per opportune combinazioni lineari di orbitali atomici di tipo 1s e 2s (σg 1s/2s e σu* 1s/2s), 2px e 2py (πu e πg*) e 2pz (σg 2p e σu* 2p).
| Molecola | Termine di stato fondamentale | De (eV) | Re (A) |
|---|---|---|---|
| H2 | 1Σ+g | 4,52 | 0,74 |
| He2 | 1Σ+g | 0.0009 | 3.00 |
| Li2 | 1Σ+g | 1.07 | 2.67 |
| Be2 | 1Σ+g | 0.10 | 2.45 |
| B2 | 3Σ-g | 3.1 | 1.59 |
| C2 | 1Σ+g | 6.3 | 1.24 |
| N2 | 1Σ+g | 9.92 | 1.10 |
| O2 | 3Σ-g | 5.21 | 1.21 |
| F2 | 1Σ+g | 1.66 | 1.41 |
| Ne2 | 1Σ+g | 0.0036 | 3.1 |
Molecole biatomiche omonucleari del terzo periodo (Na-Cl)[modifica | modifica wikitesto]
Le molecole biatomiche del terzo periodo sono state caratterizzate sperimentalmente a livello spettroscopico. Cl2 è lo stato standard per il cloro elementare.
| Molecola | Termine di stato fondamentale | De (eV) | Re (A) |
|---|---|---|---|
| Na2 | 3.0788 | ||
| Mg2 | 3.890 | ||
| Al2 | 2.466 | ||
| Si2 | 2.246 | ||
| P2 | 1.893 | ||
| S2 | 1.889 | ||
| Cl2 | 1.987 |
Molecole eteronucleari[modifica | modifica wikitesto]
Nelle molecole eteronucleari la simmetria che caratterizzava le molecole omonucleari viene a mancare, e gli orbitali non sono una pura combinazione simmetrica e antisimmetrica degli orbitali atomici. In tali molecole gli orbitali possono essere approssimati con gli autostati di una matrice quadrata di dimensione 2:[6]
dove:
è l'effettiva hamiltoniana di singolo elettrone mentre gli stati e sono gli orbitali corrispondenti rispettivamente all'atomo sinistro e destro.
Gli autovalori associati alla matrice sono:
Gli orbitali di legame e antilegame sono dati dagli autostati:
con:
per si ottiene la molecola omonucleare, e il termine rappresenta lo splitting tra l'orbitale di legame e di antilegame di una molecola omonucleare, ovvero lo splitting tra le combinazioni simmetriche e antisimmetriche.[6]
Al crescere di gli autostati di legame e di antilegame assomigliano sempre più agli orbitali e dei singoli atomi, e lo stesso avviene per i rispettivi autovalori dell'energia.[7] Quando la differenza è tale da comportare un trasferimento completo di carica tra i due atomi, il legame si dice ionico.
Moti interni[modifica | modifica wikitesto]

L'approssimazione di Born-Oppenheimer, anche detta approssimazione adiabatica, permette di poter considerare il moto dei nuclei indipendente da quello degli elettroni, dal momento che i primi sono estremamente più lenti e pesanti dei secondi. Questo rende possibile la fattorizzazione della funzione d'onda totale della molecola:[8][9]
dove il pedice e indica la funzione d'onda degli elettroni, il pedice n dei nuclei, ed e sono rispettivamente le posizioni di nuclei ed elettroni.
La funzione d'onda degli elettroni, nell'approssimazione adiabatica, soddisfa l'equazione agli autovalori:
Mentre il potenziale che guida il moto dei nuclei:
è detto potenziale adiabatico, e sta alla base della dinamica della molecola.
Dall'espressione del potenziale adiabatico si evince che la dinamica dei nuclei è guidata dall'energia fornita dall'equazione elettronica: questo termine è fondamentale, dal momento che rappresenta il "collante" che tiene uniti i nuclei degli atomi che compongono la molecola.[10]
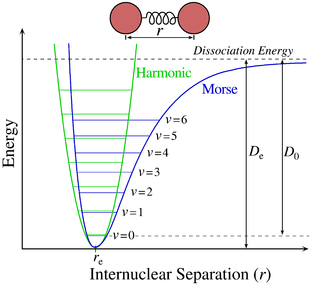
Per le molecole biatomiche il potenziale adiabatico è un potenziale armonico, e può essere approssimato dal potenziale di Morse, che a differenza dell'oscillatore armonico quantistico include esplicitamente gli effetti della rottura del legame chimico, come l'esistenza di stati non legati. Il potenziale adiabatico è indipendente dalla posizione del centro di massa della molecola e dall'orientazione della retta congiungente i due nuclei: gode quindi di invarianza rispetto alle traslazioni e alle rotazioni, e il moto dei nuclei può essere studiato come un problema a due corpi. A partire da questo approccio, l'equazione di Schrödinger può essere separata in moto radiale, dipendente dalla distanza tra i due nuclei, e moto orbitale, dipendente dal numero quantico orbitale. L'equazione di Schrödinger nel caso di un moto in un campo centrale è:
dove indica la posizione del centro di massa e la posizione relativa dei due nuclei, differenza delle rispettive posizioni.
Il problema può essere quindi separato in due equazioni, una per il centro di massa e una per la particella di massa μ che si muove in un campo centrale rispetto al centro di massa. La funzione d'onda si può quindi fattorizzare nel seguente modo: . L'equazione per , che rappresenta il problema della particella libera, fornisce l'energia traslazionale della molecola. L'equazione per si può ulteriormente fattorizzare in parte radiale, dipendente da r, e parte angolare, dipendente dalle coordinate angolari: .
La soluzione per sono le armoniche sferiche, e i rispettivi stati sono autostati del momento angolare orbitale e della sua componente lungo l'asse z.
L'equazione per è invece, detta :[11]
dove il secondo termine rappresenta il contributo energetico rotazionale , che dipende dal numero quantico orbitale l.
Il potenziale adiabatico può essere inoltre sviluppato in serie di Taylor, che troncata al secondo ordine è:[9]
dove è il valore di che minimizza , e rappresenta la posizione di equilibrio dei due nuclei. Tale espressione rappresenta un moto armonico attorno a che fornisce un contributo energetico dato dall'energia dell'equazione elettronica contenuta in e dall'energia vibrazionale .

Detta la lunghezza caratteristica data dalla relazione e detta , le soluzioni dell'equazione per sono:
dove è il polinomio di Hermite di grado .
Lo spettro energetico contiene in definitiva tre termini:
Tali termini sono i contributi energetici che caratterizzano la dinamica della molecola biatomica, e nello specifico sono:[9][12]
- Il contributo elettronico, dato dal termine di , che definisce la profondità della buca di potenziale generata dai due nuclei, responsabile del legame chimico. I livelli energetici associati a questo termine sono detti superfici adiabatiche, e corrispondono ai diversi stati energetici degli elettroni. Gli elettroni che vengono promossi da un orbitale a un altro, ad esempio da un orbitale di legame a uno di antilegame, effettuano una transizione tra due valori e del potenziale adiabatico. Tali transizioni sono dell'ordine di 10 eV, e a differenti superfici adiabatiche corrispondono anche diversi valori di . Le transizioni elettroniche tra due di tali superfici sono inoltre accompagnate da transizioni tra diversi stati vibrazionali e rotazionali.
- Il contributo vibrazionale, meno energetico del precedente, che nell'approssimazione di moto armonico fornita dall'esclusione dei termini superiori al secondo ordine nel precedente sviluppo di è dato dagli autovalori dell'oscillatore armonico quantistico:
- dove è la costante di Planck e la frequenza angolare dell'oscillazione intorno a .
- La frequenza è data da:
- con
- e la massa ridotta dell'oscillatore a due corpi, data dal rapporto tra il prodotto e la somma delle masse dei due nuclei.
- Tale contributo descrive il moto armonico dei due nuclei intorno alla posizione di equilibrio, e transizioni tra due livelli vibrazionali sono dell'ordine del decimo di eV.
- Il contributo rotazionale, il meno energetico dei tre, fornito dall'equazione angolare dell'atomo di idrogeno, pari a:
- dove è il momento angolare orbitale e il momento d'inerzia.
- Tale contributo è generalmente dell'ordine dei meV, ed è calcolato assumendo .
In conclusione, quindi, l'energia interna di una molecola biatomica è:
dove i termini sono elencati in ordine di importanza.

Spettro elettromagnetico molecolare[modifica | modifica wikitesto]
Lo spettro elettromagnetico molecolare è generato dalle transizioni tra due autostati dell'energia totale. Nel caso si studi lo spettro di emissione la molecola passa da uno stato eccitato allo stato fondamentale, mentre nel caso si studi lo spettro di assorbimento si osserva la transizione inversa. Tale passaggio comporta l'emissione o l'assorbimento di un fotone, la cui frequenza è data dalla legge di Planck:
dove è la differenza di energia tra i due stati di partenza e arrivo:
Le transizioni elettroniche dallo stato fondamentale ai primi stati eccitati sono dell'ordine di alcuni eV, e sono osservate nella regione del visibile e dell'ultravioletto dello spettro elettromagnetico, mentre le transizioni roto-vibrazionali sono osservate nella regione dell'infrarosso.[13]
Le transizioni tra due autostati dell'energia totale vengono studiate attraverso le transizioni tra autostati del momento di dipolo elettrico, definito come:[9]
con e la carica dell'elettrone.
Tale operatore è esplicitato dall'espressione:
dove è l'operatore di momento dipolare elettronico della molecola:

Ognuno dei livelli vibrazionali che caratterizzano una superficie adiabatica è associato a diversi stati rotazionali. Nel diagramma spettroscopico le transizioni rotazionali costituiscono due rami: il primo è detto R Branch, e rappresenta le transizioni rotazionali tra i numeri quantici , mentre il secondo, detto P branch, rappresenta le transizioni . Tra i due rami vi è un vuoto, motivato dal fatto che la transizione è proibita dalle regole di selezione.[14]
Quando la transizione viene effettuata da un elettrone, essa genera anche transizioni tra autostati dell'energia roto-vibrazionale dei nuclei: tali transizioni sono dette vibroniche, e sono causate dal fatto che a due differenti superfici adiabatiche corrispondono geometrie diverse della molecola. In particolare, nelle molecole biatomiche, corrispondono a distanze internucleari differenti.
Spettro nucleare[modifica | modifica wikitesto]
Nel caso di molecole biatomiche omonucleari il momento di dipolo elettrico è nullo per motivi di simmetria,[15] e questo fatto spiega la trasparenza dell'atmosfera terrestre, composta prevalentemente da O2 e N2.
Nelle molecole biatomiche eteronucleari, invece, l'elemento di matrice della componente lungo l'asse z del momento di dipolo è:[9]
dove sono gli autostati simultanei dell'energia vibrazionale e rotazionale. Lo stesso accade per le componenti x e y.
Dalle proprietà delle armoniche sferiche e dallo sviluppo di attorno alla distanza di equilibrio si ottengono le regole di selezione:
che definiscono le transizione permesse tra autostati dell'operatore associato all'osservabile dipolo elettrico.

Spettro elettronico[modifica | modifica wikitesto]
Una transizione elettronica molecolare consiste in una transizione da parte dell'elettrone tra due superfici adiabatiche. Tali transizioni sono simili a quelle atomiche, e consistono nella promozione di un elettrone da un orbitale molecolare a un altro orbitale vuoto.[13]
Le regole di selezione si ricavano osservando che l'operatore di spin totale:
commuta con l'hamiltoniana elettronica e con , l'operatore di dipolo non agisce sullo spin, e pertanto si ha che .[9]
Per l'operatore di momento angolare nelle molecole biatomiche:
solo la componente lungo l'asse z commuta con , ottenendo che , mentre per le altre due componenti si ricava che . In definitiva si ha:
Il principio di Franck Condon[modifica | modifica wikitesto]
Il principio di Franck Condon afferma la probabilità associata a una transizione vibrazionale, data da:
aumenta all'aumentare della sovrapposizione delle funzioni d'onda dei rispettivi stati iniziale e finale. Questo comporta che i livelli vibrazionali associati allo stato finale sono favoriti nel momento in cui la transizione comporta un cambiamento minimo nelle coordinate nucleari. Una conseguenza del principio è che, ad esempio, come mostrato nella figura a sinistra, se le funzioni d'onda tra lo stato fondamentale della superficie adiabatica iniziale e il secondo stato eccitato della superficie adiabatica finale si sovrappongono, tale transizione è più probabile delle altre dal momento che minimizza la variazione delle coordinate dei nuclei.
Note[modifica | modifica wikitesto]
- ^ Brehm, Mullins, Pag. 503.
- ^ Brehm, Mullins, Pag. 504.
- ^ Brehm, Mullins, Pag. 507.
- ^ Brehm, Mullins, Pag. 509.
- ^ a b Brehm, Mullins, Pag. 510.
- ^ a b Manini, Pag. 70.
- ^ Manini, Pag. 71.
- ^ Manini, Pag. 61.
- ^ a b c d e f Renzo Cimiraglia - Note al corso di Spettroscopia Molecolare (PDF), su chim183.unife.it. URL consultato il 15 novembre 2010 (archiviato dall'url originale il 2 agosto 2007).
- ^ Manini, Pag. 62.
- ^ Brehm, Mullins, Pag. 523.
- ^ Manini, Pag. 76.
- ^ a b Manini, Pag. 79.
- ^ Manini, Pag. 78.
- ^ Brehm, Mullins, Pag. 528.
Bibliografia[modifica | modifica wikitesto]
- (EN) John Brehm, William J. Mullins, Introduction To The Structure Of Matter: A Course In Modern Physics, Greenville, NC, U.S.A., John Wiley & Sons, 1989, ISBN 978-0-471-60531-7.
- (EN) Nicola Manini, Introduction to the Physics of Matter, Milano, CUSL, 2008, ISBN 978-88-8132-552-8.
- Roberto Spinicci, Elementi di Chimica, Firenze, Firenze University Press, 2009, ISBN 978-88-6453-062-8.
- (EN) Pauling, Linus, General Chemistry, New York, Dover Publications, Inc., 1970, ISBN 0-486-65622-5.
- (EN) Ebbin, Darrell, D., General Chemistry, 3rd Ed., Boston, Houghton Mifflin Co., 1990, ISBN 0-395-43302-9.
- (EN) Brown, T.L., Chemistry – the Central Science, 9th Ed., New Jersey, Prentice Hall, 2003, ISBN 0-13-066997-0.
- (EN) Chang, Raymond, Chemistry, 6th Ed., New York, McGraw Hill, 1998, ISBN 0-07-115221-0.
- (EN) Zumdahl, Steven S., Chemistry, 4th ed., Boston, Houghton Mifflin, 1997, ISBN 0-669-41794-7.
Voci correlate[modifica | modifica wikitesto]
Altri progetti[modifica | modifica wikitesto]
 Wikimedia Commons contiene immagini o altri file su molecola biatomica
Wikimedia Commons contiene immagini o altri file su molecola biatomica
Collegamenti esterni[modifica | modifica wikitesto]
- (EN) Ken Stewart, diatomic molecule, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
| Controllo di autorità | J9U (EN, HE) 987007544649405171 |
|---|
![{\displaystyle \left[{\frac {\hbar ^{2}}{2m_{e}}}\nabla _{r}^{2}-{\frac {ke^{2}}{|\mathbf {r} +\mathbf {R} /2|}}-{\frac {ke^{2}}{|\mathbf {r} -\mathbf {R} /2|}}+{\frac {ke^{2}}{R}}\right]\psi _{\mathrm {e} }(\mathbf {r} )=E_{\mathrm {e} }(\mathbf {r} )\psi _{\mathrm {e} }(\mathbf {r} )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dbdcc15a178e5f1487ae8efb1746b1a94d4898bc)


![{\displaystyle \psi _{\mathrm {\pm } }(\mathbf {r} )={\frac {1}{\sqrt {2}}}[\psi _{1s}(\mathbf {r} +\mathbf {R} /2)\pm \psi _{1s}(\mathbf {r} -\mathbf {R} /2)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fdf6c56809c63e4c6bfd05f1afb629af6a11f059)




![{\displaystyle |\psi _{\mathrm {\pm } }|^{2}={\frac {1}{2}}[\psi _{1s}^{2}(\mathbf {r} +\mathbf {R} /2)+\psi _{1s}^{2}(\mathbf {r} -\mathbf {R} /2)\pm 2\psi _{1s}(\mathbf {r} +\mathbf {R} /2)\psi _{1s}(\mathbf {r} -\mathbf {R} /2)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50a75eda255a84496516016b11905999d90085a1)
![{\displaystyle \psi _{\mathrm {S} }(1,2)={\frac {1}{\sqrt {2}}}[\psi _{1s}(\mathbf {r_{1}} -\mathbf {R} /2)\psi _{1s}(\mathbf {r_{2}} +\mathbf {R} /2)+\psi _{1s}(\mathbf {r_{2}} -\mathbf {R} /2)\psi _{1s}(\mathbf {r_{1}} +\mathbf {R} /2)]\chi ^{A}(1,2)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/909792d0f57537b94dea0a27378c910077e1d41c)
![{\displaystyle \psi _{\mathrm {T} }(1,2)={\frac {1}{\sqrt {2}}}[\psi _{1s}(\mathbf {r_{1}} -\mathbf {R} /2)\psi _{1s}(\mathbf {r_{2}} +\mathbf {R} /2)-\psi _{1s}(\mathbf {r_{2}} -\mathbf {R} /2)\psi _{1s}(\mathbf {r_{1}} +\mathbf {R} /2)]\chi ^{S}(1,2)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efa707e0f683775b3cc7ef364bdf94eb4370d291)


![{\displaystyle |\psi _{\mathrm {S,T} }|^{2}={\frac {1}{2}}[\psi _{1s}^{2}(\mathbf {r_{1}} -\mathbf {R} /2)\psi _{1s}^{2}(\mathbf {r_{2}} +\mathbf {R} /2)+\psi _{1s}^{2}(\mathbf {r_{2}} -\mathbf {R} /2)\psi _{1s}^{2}(\mathbf {r_{1}} +\mathbf {R} /2)\pm 2\psi _{1s}(\mathbf {r_{1}} -\mathbf {R} /2)\psi _{1s}(\mathbf {r_{1}} +\mathbf {R} /2)\psi _{1s}(\mathbf {r_{2}} -\mathbf {R} /2)\psi _{1s}(\mathbf {r_{2}} +\mathbf {R} /2)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d0321d97d2ee4d9fd4e369101f55dbd777cacec)
















![{\displaystyle \left[T_{\mathrm {e} }+V_{\mathrm {ne} }(\mathbf {R} ,\mathbf {r} )+V_{\mathrm {ee} }(\mathbf {r} )\right]\psi _{\mathrm {e} }(\mathbf {R} ,\mathbf {r} )=E_{\mathrm {e} }(\mathbf {R} )\psi _{\mathrm {e} }(\mathbf {R} ,\mathbf {r} )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad4ab644a0a73006f448d26d3dea2c5b0e598731)


![{\displaystyle \left[-{\frac {\hbar ^{2}}{2(M+m)}}\nabla _{\mathbf {r} _{cm}}^{2}-{\frac {\hbar ^{2}}{2\mu }}\nabla ^{2}+V_{\mathrm {ad} }(|\mathbf {r} _{rel}|)\right]\psi _{\mathrm {n} }(\mathbf {r} _{cm},\mathbf {r} _{rel})=E_{tot}\psi _{\mathrm {n} }(\mathbf {r} _{cm},\mathbf {r} _{rel})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f63a966a7e40307058884854406f9068bf7029e)









![{\displaystyle \left[-{\frac {\hbar ^{2}}{2\mu }}{\frac {d^{2}}{dr^{2}}}+{\frac {\hbar ^{2}l(l+1)}{2\mu r^{2}}}+V_{\mathrm {ad} }(|\mathbf {r} _{rel}|)\right]g=Eg}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a0d8b7c5343baef9266e16f45363c9237debc159)






































![{\displaystyle \mathbf {d} =\int {\psi _{vib}'^{*}\psi _{rot}'^{*}}\left[\int \psi _{el}^{*}\mathbf {d} \psi _{el}dx_{e}\right]\psi _{vib}\psi _{rot}d\tau =\langle {\psi _{vib}'\psi _{rot}'}|\mathbf {\mu } |\psi _{vib}\psi _{rot}\rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/16e3a71f413c36ee9c61f3107e06dcdcd39d8a6a)


















