Evezione

Con evezione, in astronomia, si intende la modificazione causata dal Sole all'orbita di rivoluzione della Luna attorno alla Terra.

L'evezione causa la variazione della longitudine celeste della Luna di circa 1.27 gradi, in un periodo di circa 31.8 giorni. Essa si presenta con una periodica variazione dell'eccentricità dell'orbita lunare e della posizione del suo perigeo, causata dall'azione del Sole.

L'evezione era conosciuta nell'antichità e la sua scoperta indirettamente potrebbe essere attribuita ad Ipparco di Nicea che influenzò gli studi di Tolomeo.^[1]

Introduzione[modifica | modifica wikitesto]

Il termine evezione deriva dal latino e ha come significato portar fuori.

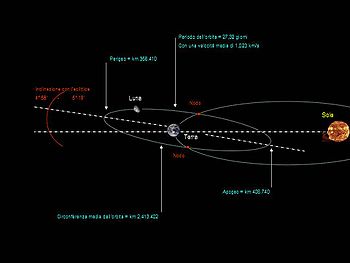
Il movimento che la Luna compie attorno alla Terra non è influenzato solamente dalla forza gravitazionale di quest'ultima, ma soprattutto da quella del Sole che risulta essere più del doppio del valore della forza attrattiva del nostro pianeta; tanto che sembrerebbe più corretto dire che il nostro satellite gira attorno al Sole ed è perturbato dalla forza d'attrazione della Terra.

L'eccentricità dell'orbita della Luna varia in continuazione grazie alla forza d'attrazione solare e queste perturbazioni causano mutamenti dell'orientamento dell'asse maggiore dell'orbita, tanto che essa avanza di 3° ogni rivoluzione, e compie un giro intero ogni 8,85 anni (spostamento della linea degli apsidi).

Siccome la Luna orbita in un piano che risulta inclinato di circa 5,14° rispetto al piano in cui orbita la Terra intorno al Sole, questi piani si intersecano i due punti (nodi) e la linea che li congiunge prende il nome di asse nodale.

A causa delle perturbazioni indotte dal Sole, ed in minima parte da Venere e da Giove, la linea dei nodi si sposta in moto diretto o retrogrado in 18,61 anni.

Espressioni[modifica | modifica wikitesto]

L'evezione in longitudine è data dall'espressione:

$+4586.45''\sin(2D-l)$

Dove D è l'elongazione media e distanza angolare della Luna dal Sole; l è l'anomalia media della Luna (distanza angolare media della Luna dal suo perigeo).

D'altra parte riprendendo da Orbita della Luna l'evezione può essere calcolata.

Il termine $+{15 \over 4}\cdot m\cdot e\cdot \mathrm {sen} ({(2-2\cdot m-c)\cdot p\cdot t-2\cdot \beta +\alpha })$ è denominato Evezione. I suoi effetti si possono considerare in due prospettive diverse:

Termine considerato per sé stesso[modifica | modifica wikitesto]

Esso è dunque un termine correttivo di

\theta =p\cdot t+{15 \over 4}\cdot m\cdot e\cdot \mathrm {sen} ({(2-2\cdot m-c)\cdot p\cdot t-2\cdot \beta +\alpha })

si definiscano le seguenti grandezze:

\mathrm {luna} =p\cdot t=

longitudine media della Luna

\mathrm {sole} =m\cdot p\cdot t+\beta =

longitudine media del Sole

\alpha '=(1-c)\cdot p\cdot t+\alpha =

longitudine media dell'asse degli apsidi

raccogliendo opportunamente i termini

\theta =p\cdot t+{15 \over 4}\cdot m\cdot e\cdot \mathrm {sen} ({2\cdot (p\cdot t-(m\cdot p\cdot t+\beta ))-(p\cdot t-(1-c)\cdot p\cdot t+\alpha )}))=

=p\cdot t+{15 \over 4}\cdot m\cdot e\cdot \mathrm {sen} ({2\cdot (luna-sole)-(luna-\alpha '}))

Gli effetti di questo termine sono:

alle sizigie, quando Sole e Luna sono allineati, cioè quando hanno la stessa longitudine, la prima parte dell'argomento del seno si annulla, e pertanto rimane $\theta =p\cdot t-{15 \over 4}\cdot m\cdot e\cdot \mathrm {sen} ({luna-\alpha '})$ , cioè la posizione “vera” della Luna è prima o dopo quella “media” a seconda del segno dell'argomento della funzione "seno";
alle Quadrature, quando Sole e Luna distano 90°, la prima parte dell'argomento del seno vale pi greco, e pertanto rimane $\theta =p\cdot t+{15 \over 4}\cdot m\cdot e\cdot \mathrm {sen} ({luna-\alpha '})$ , e le circostanze sono esattamente invertite a causa dell'inversione di segno.

In entrambi i casi la correzione globale si annulla quando la linea degli apsidi è alle sizigie o alle quadrature nello stesso momento della Luna. Nelle posizioni intermedie la natura della correzione è più complessa, ma si annulla sempre quando il Sole è a metà tra la Luna e la linea degli apsidi, o quando dista 90° o 180° da quel punto. Se:

sole={luna+\alpha ' \over 2}-r\cdot 90

dove

r={0,-1,1,2}

allora

\mathrm {sen} ({2\cdot (luna-sole)-(luna-\alpha ')})=\mathrm {sen} ({luna+\alpha '-2\cdot sole})=

=\mathrm {sen} ({r\cdot 180})=0

Termine considerato in funzione della ineguaglianza ellittica[modifica | modifica wikitesto]

Il secondo e più usuale metodo è quello di considerare gli effetti di questo termine in combinazione con i due termini della ineguaglianza ellittica, come segue: “determinare la variazione della posizione della linea degli apsidi e la variazione nella eccentricità dell'orbita della Luna, prodotta dall'evezione”. Si prendano allora assieme la “Ineguaglianza Ellittica” e la “Evezione”:

\theta =p\cdot t+2\cdot e\cdot \mathrm {sen} ({c\cdot p\cdot t-\alpha })+{5 \over 4}\cdot e^{2}\cdot \mathrm {sen} (2\cdot ({c\cdot p\cdot t-\alpha }))+{15 \over 4}\cdot m\cdot e\cdot \mathrm {sen} ({(2-2\cdot m-c)\cdot p\cdot t-2\cdot \beta +\alpha })

sia $\alpha '$ la longitudine della linea degli apsidi al tempo $t$ , nella ipotesi di avanzamento uniforme

\alpha '=(1-c)\cdot p\cdot t+\alpha

sole=m\cdot p\cdot t+\beta

allora la precedente può essere riscritta

\theta =p\cdot t+2\cdot e\cdot \mathrm {sen} ({c\cdot p\cdot t-\alpha })+{5 \over 4}\cdot e^{2}\cdot \mathrm {sen} (2\cdot ({c\cdot p\cdot t-\alpha }))+{15 \over 4}\cdot m\cdot e\cdot \mathrm {sen} ({c\cdot p\cdot t-\alpha +2\cdot (\alpha '-sole)})

combinando insieme il secondo ed il quarto termine in uno solo

2\cdot E\cdot \mathrm {sen} ({c\cdot p\cdot t-\alpha +\delta })

e si assuma

E\cdot \cos({\delta })=e+{15 \over 8}\cdot m\cdot e\cdot \cos({2\cdot (\alpha '-sole)})

E\cdot \mathrm {sen} ({\delta })={15 \over 8}\cdot m\cdot e\cdot \mathrm {sen} ({2\cdot (\alpha '-sole)})

da cui si possono ricavare $E$ e $\tan({\delta })$ ; approssimativamente vale

E=e\cdot (1+{15 \over 8}\cdot m\cdot \cos({2\cdot (\alpha '-sole)})

\delta ={15 \over 8}\cdot m\cdot \mathrm {sen} ({2\cdot (\alpha '-sole)})

il termine ${5 \over 4}\cdot e^{2}\cdot \mathrm {sen} (2\cdot ({c\cdot p\cdot t-\alpha }))$ può anche, al secondo ordine, essere espresso da

{5 \over 4}\cdot E^{2}\cdot \mathrm {sen} (2\cdot ({c\cdot p\cdot t-\alpha +\delta }))

e così le Longitudini diventano

\theta =p\cdot t+2\cdot E\cdot \mathrm {sen} ({c\cdot p\cdot t-\alpha +\delta })+{5 \over 4}\cdot E^{2}\cdot \mathrm {sen} ({2\cdot (c\cdot p\cdot t-\alpha +\delta )})

\theta =p\cdot t+2\cdot E\cdot \mathrm {sen} ({p\cdot t-\alpha '+\delta })+{5 \over 4}\cdot E^{2}\cdot \mathrm {sen} ({2\cdot (p\cdot t-\alpha '+\delta )})

Gli ultimi due termini costituiscono l'ineguaglianza ellittica di un'orbita di eccentricità $E$ e longitudine della linea degli apsidi $\alpha '-\delta$ [ $E$ è variabile nel tempo]; pertanto l'evezione, presa in unione con l'ineguaglianza ellittica, ha l'effetto di rendere l'eccentricità dell'orbita della Luna variabile, incrementandola di ${15 \over 8}\cdot m\cdot e$ quando la linea degli apsidi transita per le sizigie, e diminuendola della stessa quantità quando la linea degli apsidi passa per le quadrature; l'espressione generale dell'incremento vale

{15 \over 8}\cdot m\cdot e\cdot \cos({2\cdot (\alpha '-sole)})

un altro effetto di questo termine è quello di diminuire la longitudine dell'asse, calcolata nell'ipotesi di moto uniforme, della quantità $\delta ={15 \over 8}\cdot m\cdot \mathrm {sen} ({2\cdot (\alpha '-sole)})$ ; così l'asse della linea degli Apsidi è dietro a quello medio nel primo o il terzo quadrante quando è in anticipo rispetto al Sole, e davanti quando è nel secondo o quarto quadrante. Il ciclo di queste variazioni dovrà essere evidentemente completato in un periodo di mezza rivoluzione del Sole rispetto all'asse degli Apsidi, cioè circa in ${9 \over 16}$ di un anno.