In matematica, la trasformata di Fourier a tempo discreto, spesso abbreviata con DTFT (acronimo del termine inglese Discrete-Time Fourier Transform), è una trasformata che a partire da un segnale discreto ne fornisce una descrizione periodica nel dominio della frequenza, analogamente alla trasformata di Fourier tradizionale (definita per funzioni continue).
Si tratta di un caso particolare della trasformata zeta:
![{\displaystyle X(z)=\sum _{n=-\infty }^{\infty }x[n]\,z^{-n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a599aa526823646d32469385b73490b60e28ea7)
che si ottiene ponendo  (
( è inteso come angolo). Dal momento che
è inteso come angolo). Dal momento che  , la trasformata di Fourier a tempo discreto è la valutazione della trasformata zeta sul cerchio unitario nel piano complesso.
, la trasformata di Fourier a tempo discreto è la valutazione della trasformata zeta sul cerchio unitario nel piano complesso.
Dato un insieme di numeri interi complessi ![{\displaystyle x[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/864cbbefbdcb55af4d9390911de1bf70167c4a3d) , con
, con  , la sua trasformata di Fourier a tempo discreto è la serie:
, la sua trasformata di Fourier a tempo discreto è la serie:
![{\displaystyle X(\omega )=\sum _{n=-\infty }^{\infty }x[n]\,e^{-i\omega n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/553acaf0fb714decb09013e12275ca65bed638d7)
La trasformata inversa permette di ottenere la funzione originale a partire dalla sua trasformata:
![{\displaystyle x[n]={\frac {1}{2\pi }}\int _{2\pi }X(\omega )\cdot e^{i\omega n}d\omega }](https://wikimedia.org/api/rest_v1/media/math/render/svg/bdec9f866497246173ad9c633f12839a4a019ca7)
La trasformata di Fourier a tempo discreto ha un ruolo rilevante quando si studiano segnali campionati, ovvero segnali a tempo discreto ottenuti da un segnale a tempo continuo considerandone il valore assunto in precisi istanti di tempo, solitamente separati da un intervallo temporale fisso  . La procedura che permette di ottenere un segnale discreto a partire da uno continuo è detta campionamento, ed è alla base della conversione analogico-digitale (ADC). Essa trasforma una funzione continua
. La procedura che permette di ottenere un segnale discreto a partire da uno continuo è detta campionamento, ed è alla base della conversione analogico-digitale (ADC). Essa trasforma una funzione continua  nel segnale discreto:
nel segnale discreto:
![{\displaystyle x[n]\ {\stackrel {\text{def}}{=}}\ x(nT)\qquad \forall \,n\in \mathbb {Z} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/565f01b488cc520b3aecdf0a1d58370501a21cbd)
con  la frequenza di campionamento. Il teorema del campionamento pone un limite alla massima frequenza del segnale continuo, che non può essere superiore ad
la frequenza di campionamento. Il teorema del campionamento pone un limite alla massima frequenza del segnale continuo, che non può essere superiore ad  se si vuole evitare perdita di informazione (fenomeno di aliasing). La trasformata a tempo discreto fornisce un'approssimazione della trasformata di Fourier
se si vuole evitare perdita di informazione (fenomeno di aliasing). La trasformata a tempo discreto fornisce un'approssimazione della trasformata di Fourier  :
:

Infatti, considerando la formula di sommazione di Poisson, che mostra come ottenere una sommazione periodica di una funzione  a partire dai campioni di una funzione tempo-continua, si ha:
a partire dai campioni di una funzione tempo-continua, si ha:
![{\displaystyle X_{1/T}(f)\ {\stackrel {\mathrm {def} }{=}}\sum _{k=-\infty }^{\infty }X\left(f-k/T\right)\equiv \sum _{n=-\infty }^{\infty }\underbrace {T\cdot x(nT)} _{x[n]}\ \underbrace {e^{-i2\pi fTn}} _{{\mathcal {F}}\{\delta (t-nT)\}}\ =\ {\mathcal {F}}\left\{\sum _{n=-\infty }^{\infty }x(t)\cdot \delta (t-nT)\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/361a8cddde0bb7b75c7134e2376ba760b2dadcdb)
dove  include copie esatte di
include copie esatte di  traslate di un multiplo di
traslate di un multiplo di  e combinate per addizione. Per
e combinate per addizione. Per  sufficientemente grande il termine
sufficientemente grande il termine  può essere osservato nella regione
può essere osservato nella regione ![{\displaystyle [-f_{s}/2,f_{s}/2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b709f5f5354894fddd10bd415574d7f9483d742) , con distorsione minima o nulla. Un altro modo per verificare questo fatto è il seguente:
, con distorsione minima o nulla. Un altro modo per verificare questo fatto è il seguente:

Calcolando la trasformata di Fourier inversa di entrambi i membri dell'equazione precedente, inoltre, si ottiene il pettine di Dirac modulato:
![{\displaystyle \sum _{n=-\infty }^{\infty }x[n]\cdot \delta (t-nT)={\mathcal {F}}^{-1}\left\{X_{1/T}(f)\right\}\ {\stackrel {\mathrm {def} }{=}}\int _{-\infty }^{\infty }X_{1/T}(f)\cdot e^{i2\pi ft}df.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/67126209df0c938694ada453169eb06f1cfd05a2)
con:
![{\displaystyle x[n]=T\int _{\frac {1}{T}}X_{1/T}(f)\cdot e^{i2\pi fnT}df={\frac {1}{2\pi }}\int _{2\pi }X(\omega )\cdot e^{i\omega n}d\omega }](https://wikimedia.org/api/rest_v1/media/math/render/svg/a31004995be0386670d4d29f9b58f1d3322a79b7)
Se la successione in ingresso ![{\displaystyle x[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/864cbbefbdcb55af4d9390911de1bf70167c4a3d) è periodica con periodo N è possibile espandere il pettine di Dirac in serie di Fourier, ottenendo la trasformata discreta di Fourier (DFT):
è periodica con periodo N è possibile espandere il pettine di Dirac in serie di Fourier, ottenendo la trasformata discreta di Fourier (DFT):
![{\displaystyle {\mathcal {F}}\left\{\sum _{n=-\infty }^{\infty }x[n]\cdot \delta (t-nT)\right\}={\mathcal {F}}\left\{\underbrace {\sum _{k=-\infty }^{\infty }X[k]\cdot e^{i2\pi {\frac {k}{NT}}t}} _{Fourier\ series}\right\}=\underbrace {\sum _{k=-\infty }^{\infty }X[k]\ \cdot \ \delta \left(f-{\frac {k}{NT}}\right)} _{DTFT}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63d78c24d3d7aac90cdb8429638024c24ccba9c3)
Tale relazione mostra che la periodicità nel tempo rende discontinua la trasformata di Fourier a tempo discreto. Si può tuttavia ridurre la formula integrale in una somma di N termini:
![{\displaystyle X[k]{\stackrel {\text{def}}{=}}\ {\frac {1}{NT}}\int _{NT}\left[\sum _{n=-\infty }^{\infty }x[n]\cdot \delta (t-nT)\right]e^{-i2\pi {\frac {k}{NT}}t}dt={\frac {1}{NT}}\sum _{n=-\infty }^{\infty }x[n]\cdot \int _{NT}\delta (t-nT)\cdot e^{-i2\pi {\frac {k}{NT}}t}dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f09ef0aa3f461cd85205eaffd860e8eebef4bef)
![{\displaystyle ={\frac {1}{NT}}\underbrace {\sum _{N}x[n]\cdot e^{-i2\pi {\frac {k}{N}}n}} _{DFT}={\frac {1}{N}}\underbrace {\sum _{N}x(nT)\cdot e^{-i2\pi {\frac {k}{N}}n}} _{DFT}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a10ba17e54c790564936b4b64349e619310a0c59)
che è periodica in  .
.
Se la trasformata di Fourier a tempo discreto è una funzione continua, si usa spesso considerare un numero arbitrario di campioni di un ciclo della funzione periodica  :
:
![{\displaystyle \underbrace {X_{1/T}\left({\frac {k}{NT}}\right)} _{X_{k}}=\sum _{n=-\infty }^{\infty }x[n]\cdot e^{-i2\pi {\frac {kn}{N}}}=\underbrace {\sum _{N}x_{N}[n]\cdot e^{-i2\pi {\frac {kn}{N}}}} _{DFT}\qquad \quad k=0,\dots ,N-1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7f7f4d0909123bde1a57ef6745469c9cbe7e812)
dove  è la sommazione periodica:
è la sommazione periodica:
![{\displaystyle x_{N}[n]\ {\stackrel {\text{def}}{=}}\ \sum _{m=-\infty }^{\infty }x[n-mN]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4df36bcd8b2a0a08f0fa5da68ac6f0ee66ab31ba)
La successione  è l'inversa della trasformata discreta di Fourier. In questo modo il campionamento così effettuato comporta che la trasformata inversa sia periodica.
è l'inversa della trasformata discreta di Fourier. In questo modo il campionamento così effettuato comporta che la trasformata inversa sia periodica.
Per valutare numericamente un ciclo di  è richiesta una successione
è richiesta una successione ![{\displaystyle x[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/864cbbefbdcb55af4d9390911de1bf70167c4a3d) di lunghezza finita. A tal fine spesso si tronca una successione per mezzo di una funzione finestra di lunghezza opportuna.[1]
[2]
di lunghezza finita. A tal fine spesso si tronca una successione per mezzo di una funzione finestra di lunghezza opportuna.[1]
[2]
Siano  il dominio tempo-discreto,
il dominio tempo-discreto,  la frequenza angolare (un numero reale in
la frequenza angolare (un numero reale in  misurato in radianti / campione),
misurato in radianti / campione), ![{\displaystyle u[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6f1362207606428a09d907db25527859eab6ac3) il gradino di Heaviside tempo-discreto,
il gradino di Heaviside tempo-discreto,  la funzione sinc normalizzata,
la funzione sinc normalizzata,  la delta di Dirac,
la delta di Dirac, ![{\displaystyle \delta [n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2a6caf535cb44fa3526b2f320330a805edfdfaa) la delta di Kronecker,
la delta di Kronecker,  la funzione rettangolo:
la funzione rettangolo:
![{\displaystyle \mathrm {rect} (t)=\sqcap (t)={\begin{cases}0&{\mbox{if }}|t|>{\frac {1}{2}}\\[3pt]{\frac {1}{2}}&{\mbox{if }}|t|={\frac {1}{2}}\\[3pt]1&{\mbox{if }}|t|<{\frac {1}{2}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3585cde90bc1dfbce7b14531690022ad0a7b3a6)
e  la funzione triangolo:
la funzione triangolo:

Dominio temporale
![{\displaystyle x[n]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b575dce543a2cf10a5a3e108204b928c2c9aaa54)
|
Dominio della frequenza

|
Remarks
|
![{\displaystyle \delta [n]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1553d02b03c2a79a43f7862ebfb8352705b0b87c)
|

|
|
![{\displaystyle \delta [n-M]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2dd610c46bdeb2682e719b6a0b445c1cf1893639)
|

|
 intero intero
|
![{\displaystyle \sum _{m=-\infty }^{\infty }\delta [n-Mm]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e96f3a5de2797d89e30f9856c0da6683218f006)
|

|
 intero intero
|
![{\displaystyle u[n]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d2911183bef1ad935d3bc8b5c1be97bac439b7f)
|

|
Il termine  deve essere interpretato come una distribuzione. deve essere interpretato come una distribuzione.
|
![{\displaystyle a^{n}u[n]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e544c0a61b9fba33dac991628cf707c2d38ad1eb)
|

|

|

|

|

|

|
![{\displaystyle \pi \left[\delta (\omega -a)+\delta (\omega +a)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b949fed13f25129a9f8634cb4c0aa34354b0320a)
|

|

|
![{\displaystyle {\frac {\pi }{i}}\left[\delta (\omega -a)-\delta (\omega +a)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b48e8676730fb37bcadaea9b1bb342d107cf2f9)
|

|
![{\displaystyle \mathrm {rect} \left[{(n-M/2) \over M}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4fa40f5391166dc137b30a45584c1de1a33b2f8c)
|
![{\displaystyle {\sin[\omega (M+1)/2] \over \sin(\omega /2)}\,e^{-i\omega M/2}\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd210b6fc5675148688475cb8485b49f0b065815)
|
 intero intero
|
![{\displaystyle \operatorname {sinc} [(a+n)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3526652071fa8be34f6bccac88dc94260441a47f)
|

|

|

|

|

|

|

|

|

|

|
Filtro differenziatore
|
![{\displaystyle {\frac {W}{(n+a)}}\left\{\cos[\pi W(n+a)]-\operatorname {sinc} [W(n+a)]\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7d4cd8e41d9e483f5d90da18cff3661d914ce9b)
|

|

|
![{\displaystyle {\frac {1}{\pi n^{2}}}[(-1)^{n}-1]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b97d9986fb5b086ebd0c5302cfbd88c6e4d9e236)
|

|
|

|

|
Trasformata di Hilbert
|
![{\displaystyle {\frac {C(A+B)}{2\pi }}\cdot \operatorname {sinc} \left[{\frac {A-B}{2\pi }}n\right]\cdot \operatorname {sinc} \left[{\frac {A+B}{2\pi }}n\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38083aff1d4f22b4848dfafdc988b43142f7c472)
|
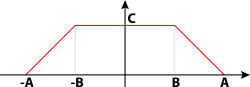
|

|
Siano  la convoluzione discreta di due successioni e
la convoluzione discreta di due successioni e ![{\displaystyle x[n]^{*}\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e49908fe3dfbd435e478d58b4c10c47e3a609c96) il complesso coniugato di
il complesso coniugato di ![{\displaystyle x[n]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91384637c5188ffed9b7929f145a78fb314c4141) .
.
| Proprietà
|
Dominio temporale ![{\displaystyle x[n]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91384637c5188ffed9b7929f145a78fb314c4141)
|
Dominio della frequenza 
|
Remarks
|
| Linearità
|
![{\displaystyle ax[n]+by[n]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c30c8f75093b9bafb5c5bde1392348701ce3be0)
|

|
|
| Traslazione temporale
|
![{\displaystyle x[n-k]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3bfc2b24164de1192ea1e17a90312a3e045911e)
|

|
 intero intero
|
| Traslazione in frequenza
|
![{\displaystyle x[n]e^{ian}\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5f540caf14c269c45b6b5d32ceb555ce8841bae)
|

|

|
| Inversione temporale
|
![{\displaystyle x[-n]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61499a6c6544d338cf6ac340b27ad734c4daba05)
|

|
|
| Coniugazione temporale
|
![{\displaystyle x[n]^{*}\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e49908fe3dfbd435e478d58b4c10c47e3a609c96)
|

|
|
| Inversione temporale e coniugazione
|
![{\displaystyle x[-n]^{*}\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb208f439fc83acd99c3db8d63304b65890993c4)
|

|
|
| Derivata
|
![{\displaystyle {\frac {n}{i}}x[n]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2eb71af662480e119b9bd16ff2e4c49151ab4b9)
|

|
|
| Integrale
|
![{\displaystyle {\frac {i}{n}}x[n]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/384ec2e6f1fb841111d00c800196000a4d406964)
|

|
|
| Convoluzione
|
![{\displaystyle x[n]*y[n]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e3b1fd5ad225be66dfa022f43a3333b08fb3fb7)
|

|
|
| Moltiplicazione
|
![{\displaystyle x[n]\cdot y[n]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3e208ac041ff192194184d3c708d7789f9c9178)
|

|
Convoluzione periodica
|
| Cross-correlazione
|
![{\displaystyle \rho _{xy}[n]=x[-n]^{*}*y[n]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37d82c9624d4b16650c5652c000d0bb459f794c6)
|

|
|
| Teorema di Parseval
|
![{\displaystyle E=\sum _{n=-\infty }^{\infty }{x[n]\cdot y^{*}[n]}\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4441b0f623efac9e5784561b56bb587551ffd43d)
|

|
|
La trasformata può essere inoltre decomposta sia in parte reale e immaginaria, sia in due funzioni rispettivamente pari e dispari:

Dominio del tempo
![{\displaystyle x[n]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91384637c5188ffed9b7929f145a78fb314c4141)
|
Dominio della frequenza

|
![{\displaystyle x^{*}[n]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4793a5489c4d67f5ffcc700e9ba06acd87e231c3)
|

|
![{\displaystyle x^{*}[-n]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34e0bcbaa111fee79bfcf34b83f9f3b6303ddaed)
|

|
- ^
Charles Constantine Gumas, Window-presum FFT achieves high-dynamic range, resolution, in Personal Engineering & Instrumentation News, luglio 1997, pp. 58–64.
- ^
Richard G. Lyons, DSP Tricks: Building a practical spectrum analyzer, su eetimes.com, EE Times, giugno 2008.
- Alan V. Oppenheim and Ronald W. Schafer, Discrete-Time Signal Processing, 2nd Edition, Prentice Hall Signal Processing Series, 1999, ISBN 0-13-754920-2.
- William McC. Siebert, Circuits, Signals, and Systems, MIT Electrical Engineering and Computer Science Series. Cambridge, MA, MIT Press, 1986.
- Boaz Porat, A Course in Digital Signal Processing, John Wiley and Sons, 1941, pp. 27–29 and 104–105, ISBN 0-471-14961-6.

![{\displaystyle X(z)=\sum _{n=-\infty }^{\infty }x[n]\,z^{-n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a599aa526823646d32469385b73490b60e28ea7)



![{\displaystyle x[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/864cbbefbdcb55af4d9390911de1bf70167c4a3d)

![{\displaystyle X(\omega )=\sum _{n=-\infty }^{\infty }x[n]\,e^{-i\omega n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/553acaf0fb714decb09013e12275ca65bed638d7)
![{\displaystyle x[n]={\frac {1}{2\pi }}\int _{2\pi }X(\omega )\cdot e^{i\omega n}d\omega }](https://wikimedia.org/api/rest_v1/media/math/render/svg/bdec9f866497246173ad9c633f12839a4a019ca7)


![{\displaystyle x[n]\ {\stackrel {\text{def}}{=}}\ x(nT)\qquad \forall \,n\in \mathbb {Z} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/565f01b488cc520b3aecdf0a1d58370501a21cbd)





![{\displaystyle X_{1/T}(f)\ {\stackrel {\mathrm {def} }{=}}\sum _{k=-\infty }^{\infty }X\left(f-k/T\right)\equiv \sum _{n=-\infty }^{\infty }\underbrace {T\cdot x(nT)} _{x[n]}\ \underbrace {e^{-i2\pi fTn}} _{{\mathcal {F}}\{\delta (t-nT)\}}\ =\ {\mathcal {F}}\left\{\sum _{n=-\infty }^{\infty }x(t)\cdot \delta (t-nT)\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/361a8cddde0bb7b75c7134e2376ba760b2dadcdb)




![{\displaystyle [-f_{s}/2,f_{s}/2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b709f5f5354894fddd10bd415574d7f9483d742)

![{\displaystyle \sum _{n=-\infty }^{\infty }x[n]\cdot \delta (t-nT)={\mathcal {F}}^{-1}\left\{X_{1/T}(f)\right\}\ {\stackrel {\mathrm {def} }{=}}\int _{-\infty }^{\infty }X_{1/T}(f)\cdot e^{i2\pi ft}df.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/67126209df0c938694ada453169eb06f1cfd05a2)
![{\displaystyle x[n]=T\int _{\frac {1}{T}}X_{1/T}(f)\cdot e^{i2\pi fnT}df={\frac {1}{2\pi }}\int _{2\pi }X(\omega )\cdot e^{i\omega n}d\omega }](https://wikimedia.org/api/rest_v1/media/math/render/svg/a31004995be0386670d4d29f9b58f1d3322a79b7)
![{\displaystyle {\mathcal {F}}\left\{\sum _{n=-\infty }^{\infty }x[n]\cdot \delta (t-nT)\right\}={\mathcal {F}}\left\{\underbrace {\sum _{k=-\infty }^{\infty }X[k]\cdot e^{i2\pi {\frac {k}{NT}}t}} _{Fourier\ series}\right\}=\underbrace {\sum _{k=-\infty }^{\infty }X[k]\ \cdot \ \delta \left(f-{\frac {k}{NT}}\right)} _{DTFT}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63d78c24d3d7aac90cdb8429638024c24ccba9c3)
![{\displaystyle X[k]{\stackrel {\text{def}}{=}}\ {\frac {1}{NT}}\int _{NT}\left[\sum _{n=-\infty }^{\infty }x[n]\cdot \delta (t-nT)\right]e^{-i2\pi {\frac {k}{NT}}t}dt={\frac {1}{NT}}\sum _{n=-\infty }^{\infty }x[n]\cdot \int _{NT}\delta (t-nT)\cdot e^{-i2\pi {\frac {k}{NT}}t}dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f09ef0aa3f461cd85205eaffd860e8eebef4bef)
![{\displaystyle ={\frac {1}{NT}}\underbrace {\sum _{N}x[n]\cdot e^{-i2\pi {\frac {k}{N}}n}} _{DFT}={\frac {1}{N}}\underbrace {\sum _{N}x(nT)\cdot e^{-i2\pi {\frac {k}{N}}n}} _{DFT}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a10ba17e54c790564936b4b64349e619310a0c59)


![{\displaystyle \underbrace {X_{1/T}\left({\frac {k}{NT}}\right)} _{X_{k}}=\sum _{n=-\infty }^{\infty }x[n]\cdot e^{-i2\pi {\frac {kn}{N}}}=\underbrace {\sum _{N}x_{N}[n]\cdot e^{-i2\pi {\frac {kn}{N}}}} _{DFT}\qquad \quad k=0,\dots ,N-1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7f7f4d0909123bde1a57ef6745469c9cbe7e812)

![{\displaystyle x_{N}[n]\ {\stackrel {\text{def}}{=}}\ \sum _{m=-\infty }^{\infty }x[n-mN]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4df36bcd8b2a0a08f0fa5da68ac6f0ee66ab31ba)



![{\displaystyle u[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6f1362207606428a09d907db25527859eab6ac3)


![{\displaystyle \delta [n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2a6caf535cb44fa3526b2f320330a805edfdfaa)

![{\displaystyle \mathrm {rect} (t)=\sqcap (t)={\begin{cases}0&{\mbox{if }}|t|>{\frac {1}{2}}\\[3pt]{\frac {1}{2}}&{\mbox{if }}|t|={\frac {1}{2}}\\[3pt]1&{\mbox{if }}|t|<{\frac {1}{2}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3585cde90bc1dfbce7b14531690022ad0a7b3a6)


![{\displaystyle x[n]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b575dce543a2cf10a5a3e108204b928c2c9aaa54)

![{\displaystyle \delta [n]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1553d02b03c2a79a43f7862ebfb8352705b0b87c)

![{\displaystyle \delta [n-M]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2dd610c46bdeb2682e719b6a0b445c1cf1893639)


![{\displaystyle \sum _{m=-\infty }^{\infty }\delta [n-Mm]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e96f3a5de2797d89e30f9856c0da6683218f006)

![{\displaystyle u[n]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d2911183bef1ad935d3bc8b5c1be97bac439b7f)


![{\displaystyle a^{n}u[n]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e544c0a61b9fba33dac991628cf707c2d38ad1eb)






![{\displaystyle \pi \left[\delta (\omega -a)+\delta (\omega +a)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b949fed13f25129a9f8634cb4c0aa34354b0320a)

![{\displaystyle {\frac {\pi }{i}}\left[\delta (\omega -a)-\delta (\omega +a)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b48e8676730fb37bcadaea9b1bb342d107cf2f9)
![{\displaystyle \mathrm {rect} \left[{(n-M/2) \over M}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4fa40f5391166dc137b30a45584c1de1a33b2f8c)
![{\displaystyle {\sin[\omega (M+1)/2] \over \sin(\omega /2)}\,e^{-i\omega M/2}\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd210b6fc5675148688475cb8485b49f0b065815)
![{\displaystyle \operatorname {sinc} [(a+n)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3526652071fa8be34f6bccac88dc94260441a47f)









![{\displaystyle {\frac {W}{(n+a)}}\left\{\cos[\pi W(n+a)]-\operatorname {sinc} [W(n+a)]\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7d4cd8e41d9e483f5d90da18cff3661d914ce9b)


![{\displaystyle {\frac {1}{\pi n^{2}}}[(-1)^{n}-1]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b97d9986fb5b086ebd0c5302cfbd88c6e4d9e236)



![{\displaystyle {\frac {C(A+B)}{2\pi }}\cdot \operatorname {sinc} \left[{\frac {A-B}{2\pi }}n\right]\cdot \operatorname {sinc} \left[{\frac {A+B}{2\pi }}n\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38083aff1d4f22b4848dfafdc988b43142f7c472)


![{\displaystyle x[n]^{*}\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e49908fe3dfbd435e478d58b4c10c47e3a609c96)
![{\displaystyle x[n]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91384637c5188ffed9b7929f145a78fb314c4141)

![{\displaystyle ax[n]+by[n]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c30c8f75093b9bafb5c5bde1392348701ce3be0)

![{\displaystyle x[n-k]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3bfc2b24164de1192ea1e17a90312a3e045911e)

![{\displaystyle x[n]e^{ian}\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5f540caf14c269c45b6b5d32ceb555ce8841bae)

![{\displaystyle x[-n]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61499a6c6544d338cf6ac340b27ad734c4daba05)


![{\displaystyle x[-n]^{*}\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb208f439fc83acd99c3db8d63304b65890993c4)

![{\displaystyle {\frac {n}{i}}x[n]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2eb71af662480e119b9bd16ff2e4c49151ab4b9)

![{\displaystyle {\frac {i}{n}}x[n]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/384ec2e6f1fb841111d00c800196000a4d406964)

![{\displaystyle x[n]*y[n]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e3b1fd5ad225be66dfa022f43a3333b08fb3fb7)

![{\displaystyle x[n]\cdot y[n]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3e208ac041ff192194184d3c708d7789f9c9178)

![{\displaystyle \rho _{xy}[n]=x[-n]^{*}*y[n]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37d82c9624d4b16650c5652c000d0bb459f794c6)

![{\displaystyle E=\sum _{n=-\infty }^{\infty }{x[n]\cdot y^{*}[n]}\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4441b0f623efac9e5784561b56bb587551ffd43d)



![{\displaystyle x^{*}[n]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4793a5489c4d67f5ffcc700e9ba06acd87e231c3)

![{\displaystyle x^{*}[-n]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34e0bcbaa111fee79bfcf34b83f9f3b6303ddaed)
