Trasformata di Hilbert

La trasformata di Hilbert è una trasformata integrale, definita per un segnale generico $x(t)$ come:

${\hat {x}}(t)\equiv {\mathcal {H}}\{x(t)\}=x(t)*h_{H}(t)={\text{p.v.}}\int _{-\infty }^{+\infty }x(\tau )h_{H}(t-\tau )\,d\tau ={\frac {1}{\pi }}\ {\text{p.v.}}\int _{-\infty }^{+\infty }{\frac {x(\tau )}{t-\tau }}\,d\tau ,\quad t\in (-1,+1),$

dove ${\hat {x}}(t)$ è la funzione o segnale trasformato; $h_{H}(t)={\frac {1}{\pi t}}=\delta (jt)$ è la risposta impulsiva del filtro di Hilbert e il prefisso "p.v." indica che l'integrale deve esistere come valore principale di Cauchy.

La trasformata di Hilbert è una trasformata integrale, ossia un'applicazione, generalmente lineare, di uno spazio di funzioni su un altro spazio di funzioni, realizzata con un integrale. Le trasformate integrali sono utili per ridurre equazioni differenziali lineari a equazioni algebriche e per l'analisi dei segnali. La trasformazione è invertibile. L'inverso è un'applicazione tre volte. Una doppia applicazione produce un orientamento invertito.

In particolare, il principale impiego della trasformata di Hilbert è nel settore delle telecomunicazioni, poiché consente di adattare un segnale o funzione di $t$ al canale di comunicazione che consente di trasmetterlo in un range o intervallo prefissato di frequenze (banda del canale di comunicazione): ciò avviene tramite lo sviluppo in componenti analogiche di bassa frequenza. Viene impiegata anche in ambito militare nei sonar per la collimazione dei bersagli.

Si osservi che l'operazione $x(t)*y(t)$ è l'operazione di convoluzione tra 2 segnali $x(t)$ e $y(t)$.

Applicazione tecnica della trasformata di Hilbert per il sonar

Sottomarino Sauro con sonar di navigazione.

La collimazione di un bersaglio con il sonar, eseguita con i sistemi di correlazione, viene evidenziata dal massimo d'ampiezza delle loro funzioni .

La collimazione in correlazione può essere migliorata mediante l'algoritmo che va sotto il nome di trasformata di Hilbert.

Con l'impiego dell'algoritmo citato si realizza un sistema di collimazione sonar con la trasformata di Hilbert in grado di determinare con precisione sia la posizione angolare di un bersaglio navale, sia l'indicazione delle sue accostate.

Funzione di correlazione e trasformata

Con i metodi di correlazione che elaborano i segnali idrofonici generati dai bersagli si ha la loro collimazione lavorando su di una funzione il cui massimo è incerto e tondeggiante, ciò non agevola la precisione di misura della sua posizione angolare rispetto all'asse longitudinale del sottomarino, non si ha inoltre nessuna indicazione dell'accostamento del bersaglio.

La trasformata di Hilbert modifica la funzione di correlazione dal suo massimo ad un passaggio per lo zero.

La trasformata attraversa il livello zero passando da valori positivi a valori negativi, è pertanto più agevole la collimazione del bersaglio nel punto di zero; da ciò scaturisce inoltre la possibilità del rilievo del senso del suo accostamento.

Aspetto matematico

L'aspetto matematico presuppone che la funzione di correlazione di base sia a segnali limitati d'ampiezza e che i due segnali applicati al correlatore abbiano ritardo $0$.

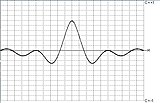
• C (tau) e trasformata HC(tau)
• 
  Funzione di correlazione $C(\tau )$: il tratto di curva attorno al massimo mostra il profilo di una funzione sinusoidale
• 
  Trasformata di Hilbert $HC(\tau )$ passante per lo zero.

La funzione di correlazione è definita nel seguente modo:

$C(\tau )={\frac {2}{\pi }}\arcsin \left(K{\frac {\sin(2\pi DF\tau )}{2\pi DF\tau }}\cos(2\pi F_{o}\tau )\right),$

dove

$f_{1}$ è la frequenza inferiore della banda di ricezione;

$f_{2}$ è la frequenza superiore della banda di ricezione;

$DF={\frac {f_{2}-f_{1}}{2}};$

$F_{o}={\frac {f_{1}+f_{2}}{2}};$

$S/N$ è il rapporto segnale/disturbo (grandezze lineari);

$K={\frac {1}{1+(N/S)^{2}}}.$

è trasformabile secondo Hilbert con l'integrale:

$HC(\tau )={\frac {1}{\pi }}\int _{-\infty }^{+\infty }{\frac {C(\tau )}{t-\tau }}\,d\tau$

la $HC(\tau )$, in base all'integrale dato, assume la forma:

$HC(\tau )={\frac {2}{\pi }}\arcsin \left(K{\frac {\sin(2\pi DF\tau )}{2\pi DF\tau }}\sin(2\pi F_{o}\tau )\right).$

La $HC(\tau )$ si diversifica dalla $C(\tau )$ per avere la funzione in coseno trasformata in funzione seno.

Hardware di trasformazione da C a HC

Schema a blocchi di un correlatore per il computo della $C(\tau )$

Un ricevitore in correlazione da laboratorio che computa la $C(\tau )$ dei segnali applicati è formato da:

• una struttura di ritardo;
• due circuiti di limitazione d'ampiezza;
• un circuito di moltiplicazione digitale (nor esclusivo);
• un circuito integratore dal quale si preleva il segnale $C(\tau ).$

Per la trasformazione del ricevitore in correlazione in circuito in grado di computare la trasformata di Hilbert è necessario modificare il ricevitore introducendo, sui segnali d'ingresso, uno sfasamento di $90$° per tutte le frequenze comprese nella banda di ricezione.

Schema a blocchi di un correlatore per il computo della $HC(\tau )$

La modifica vede:

• lo sfasatore di $90$° a larga banda;
• la struttura di ritardo;
• i circuiti di limitazione d'ampiezza;
• il circuito di moltiplicazione digitale (nor esclusivo);
• il circuito integratore dal quale si preleva il segnale $C(\tau )$.

Applicazioni della HC(τ)

Elenco di alcune applicazioni della trasformata di Hilbert per l'impiego sui sonar:

• Ricezione in passivo: circuiti RLI (Right Left Indicator), sistema per il controllo delle accostate del bersaglio che genera rumore.
• Ricezione in attivo: circuiti BDI (Bearing Deviationd Indicator), sistema per il controllo delle accostate del bersaglio con l'elaborazione del suo eco.
• Funzioni d'inseguimento automatico dei bersagli per il controllo della movimentazione di sistemi elettromeccanici.

Note

Annotazioni

Fonti

Bibliografia

• (EN) A.Papoulis, The Fourier integral and its applications, New York, Mc Graw-Hill company., 1962.
• (EN) J.W. Horton, Foundamentals of Sonar, Annapolis, Maryland, idUnited States Naval Institute, 1959.
• C. Del Turco, La correlazione, Tip. Moderna La Spezia, 1992.

Altri progetti

Altri progetti

• Wikimedia Commons

• Wikimedia Commons contiene immagini o altri file su trasformata di Hilbert

Collegamenti esterni

• (EN) Eric W. Weisstein, Trasformata di Hilbert, su MathWorld, Wolfram Research.
• N° FASCI Selenia
• Sonar FALCON
• Schemi sonar FALCON
• Testo discorsivo sul sonar
• Testo tecnico sulla Correlazione