Magnitudine assoluta

In astronomia, la magnitudine assoluta (detta anche luminosità assoluta) è la magnitudine apparente (m) che un oggetto avrebbe se si trovasse ad una distanza dall'osservatore di 10 parsec o 1 Unità Astronomica a seconda del tipo di oggetto (stellare/galattico o corpo del Sistema solare). Più semplicemente, è una misura della luminosità intrinseca di un oggetto, senza tener conto delle condizioni in cui si trova l'osservatore. Più un oggetto è intrinsecamente luminoso, più la sua magnitudine assoluta è numericamente bassa, anche negativa.

Nel definire la magnitudine assoluta, è necessario specificare il tipo di radiazione elettromagnetica che viene misurata. Se ci si riferisce al totale dell'energia emessa, il termine corretto è magnitudine bolometrica. Mentre se si considera lo spettro del visibile si parla di magnitudine assoluta visuale.

Stelle e galassie (M)

Nell'astronomia stellare e galattica la distanza standard è di 10 parsec (circa 32,6 anni luce o 3 × 10¹⁴ km). Questa magnitudine assoluta è indicata con il simbolo M. Per gli oggetti molto vasti come le galassie ci si riferisce un oggetto di pari luminosità intrinseca ma di aspetto puntiforme.

Molte stelle visibili ad occhio nudo hanno magnitudini assolute che sarebbero capaci di formare ombre da una distanza di 10 parsec: Rigel (- 6,7), Deneb (- 8,5), Naos (- 7,3), e Betelgeuse (- 5,6). Per confronto, Sirio ha una magnitudine assoluta di 1,4 e il Sole ha una magnitudine assoluta di circa 4,5. Le magnitudini assolute delle stelle in genere sono comprese tra - 10 e + 17. Proxima Centauri, una Nana rossa che è la stella più vicina alla Terra dopo il Sole, ha una magnitudine assoluta di 15,4.

Confrontando invece con le magnitudini apparenti (cioè quello che si vede osservando il cielo notturno), Sirio è - 1,4. Venere arriva a - 4,3 al suo massimo e la Luna piena è - 12. L'ultimo oggetto con una magnitudine comparabile alla magnitudine assoluta delle stelle nominate più sopra fu visibile come una supernova circa mille anni fa; il suo resto è la nebulosa del Granchio, M1. Gli astronomi cinesi riferirono di poter leggere usando la sua luce, di vedere ombre causate da essa e di poterla osservare durante il giorno.

Il diagramma H-R lega la magnitudine assoluta con la luminosità, la classificazione stellare e la temperatura superficiale.

Ricavare M da m

Per approfondire, vedi la voce magnitudine apparente.

Conosciuta la magnitudine apparente (m) è possibile calcolare la magnitudine assoluta (M) con la formula:

$\ M = m +5 - 5 \log_{10}d$

dove $\ d$ è la distanza dell'oggetto espressa in parsec.

Stelle variabili

Numerose stelle hanno una magnitudine variabile nel tempo. In alcune di queste le variazioni dipendono dalla loro magnitudine assoluta, e sono quindi estremamente utili per il calcolo delle distanze: osservando il periodo di luminosità, se ne ricava la magnitudine assoluta, e confrontandola con quella apparente si può calcolarne immediatamente la distanza. Tra questi tipi di stelle, le più importanti sono le Cefeidi (così chiamate perché la prima stella di questo tipo fu scoperta nella costellazione di Cefeo.

Corpi del sistema solare (H)

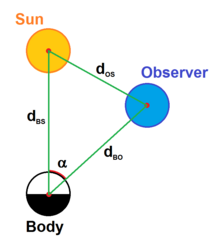
Per pianeti, comete e asteroidi si usa una differente definizione di magnitudine assoluta, perché quella descritta sopra sarebbe così bassa da essere ben poco utile. Per questi oggetti, la magnitudine assoluta (H) è la magnitudine apparente che l'oggetto avrebbe se si trovasse ad 1 Unità Astronomica sia dal Sole che dalla Terra, con un angolo di fase di zero gradi (insomma osservandolo dal centro del Sole). Questo è fisicamente impossibile, ma è conveniente dal punto di vista del calcolo.

Meteore

Per una meteora, la distanza standard è un'altezza di 100 km allo zenit dell'osservatore.

Ricavare H da M e viceversa

Per convertire la magnitudine assoluta M in magnitudine assoluta H sottrarre 31,57. Per passare da H a M aggiungere la stessa quantità.

Voci correlate

• Magnitudine apparente, per una descrizione più dettagliata dei problemi di misurazione della luminosità di un oggetto lontano
• Jansky, unità di misura di preferita dai radio astronomi
• Luminosità superficiale, per oggetti estesi
• Lista delle stelle più luminose conosciute

Portale Astronomia

Portale Fisica

Portale Stelle