Prospettiva

La prospettiva è un insieme di proiezioni e di procedimenti di carattere geometrico-matematico che consentono di rendere l'immagine di una figura dello spazio su un piano, proiettando la stessa da un centro di proiezione posto a distanza finita, e dove detto centro è il punto di vista. Così, cambiando il punto di vista, cambia anche la prospettiva e viceversa.

Nello specifico, si tratta di una proiezione centrale o conica, della prospettiva. La specificazione è utile per distinguerla dalla prospettiva parallela, modo alternativo, anche se non di uso corrente, di chiamare le assonometrie. La parziale comunanza dei termini è dovuta al fatto che l'assonometria, per motivi strutturali legati alla determinazione dell'immagine su un solo piano, può essere vista come un caso particolare della prospettiva in cui il centro di proiezione, anziché essere un punto proprio, è all'infinito.

Anche per la prospettiva, configurandosi come diretta applicazione di uno dei metodi di rappresentazione appartenenti al corpo della geometria descrittiva, vale il requisito della sostituibilità fra la figura obiettiva e la sua proiezione. Ciò significa che data la figura nello spazio, deve sempre essere possibile determinarne l'immagine su di un piano e viceversa, data l'immagine, si deve poter risalire alla configurazione della figura nello spazio (al punto di vista o al punto di proiezione).

Tale reciprocità non è ottenibile in misura piena e immediata, come avviene per le proiezioni parallele, perché nella prospettiva centrale uno stesso oggetto, proiettato da un medesimo punto di vista su piani a differente distanza da esso, dà luogo a immagini simili ma di dimensioni diverse. Per risalire quindi alle reali dimensioni dell'oggetto occorre l'introduzione nell'immagine di elementi metrici ausiliari di riferimento che permettano di risolvere il problema. Nell'ambito della prospettiva il requisito della sostituibilità trova una significativa applicazione nella fotogrammetria, che in alcuni casi si avvale di procedimenti particolari anche di notevole complessità.

Il famoso Golden Gate Bridge di San Francisco. Una normale fotografia è in tutto assimilabile a una prospettiva^[1]. Nell'apparato della macchina fotografica, il quadro è la superficie sensibile della pellicola, il centro di proiezione il secondo punto nodale dell'obiettivo, mentre la distanza fra il centro e l'immagine è data dalla distanza focale principale dell'obiettivo; le rette proiettanti sono i raggi luminosi.

Etimologia

Dal punto di vista linguistico, il vocabolo "prospettiva" è la forma femminile sostantivata di "prospettivo", derivante a sua volta dal latino tardo "prospectivus", "che assicura la vista"^[2]. Nel campo degli studi ottici medievali la perspectiva indicava l'ottica stessa (perspectiva naturalis)^[3], intesa come percezione visiva. In particolare indicava la pratica per misurare le distanze e le lunghezze inaccessibili tramite un rilevamento indiretto^[4].

Storia

Antichità

La prospettiva fu il primo tra i metodi usati di rappresentazione a essere, per così dire, codificato. Non si trovano però riferimenti a essa negli antichi trattati classici di geometria e la perdita totale della grande pittura parietale greca non ci permette di sapere con sicurezza se quei pittori adoperassero o meno procedimenti tecnici utili a una corretta rappresentazione prospettica del reale. Dai cospicui resti di pittura romana pervenutaci, in gran parte derivati da soggetti ellenistici, si nota una matura capacità di ottenere scorci, ma il disegno delle linee che definiscono gli ambienti architettonici è molto approssimativo e lascia intendere che, almeno nell'ambiente romano, i metodi operativi per ottenere gli effetti prospettici nelle immagini erano del tutto intuitivi.

Medioevo

Nel periodo bizantino e durante l'alto Medioevo, i problemi connessi con la mimesi nella rappresentazione furono quasi completamente trascurati, in quanto il fine delle arti figurative era evocare il trascendente, e per questo si elaborarono stilemi anche assai raffinati, tralasciando però, anche volutamente, la ricerca di effetti di un oggettivo realismo nelle immagini. Solo a partire dalla fine del Duecento, e soprattutto con l'opera pittorica di Giotto, la restituzione illusionistica della realtà e la corposità delle figure tornò a essere un tema di interesse primario e un obiettivo da raggiungere nelle rappresentazioni. Era perciò inevitabile che si sviluppasse la ricerca di espedienti e di procedimenti atti a ottenere delle figurazioni in qualche modo corrispondenti al tipo di percezione visiva dell'essere umano. Già verso metà del XIV secolo si era giunti a risultati tutt'altro che trascurabili, come dimostra l'Annunciazione di Ambrogio Lorenzetti conservata alla Pinacoteca Nazionale di Siena, dipinta su tavola nel 1344.

Primo Rinascimento

All'inizio del Quattrocento, a opera del grande architetto fiorentino Filippo Brunelleschi si ebbe un primo salto di qualità, si può dire di ordine scientifico. Attraverso studi ed esperienze condotte con l'aiuto di strumenti ottici, Brunelleschi pervenne ad un procedimento metodologico per rappresentare gli edifici in prospettiva, che illustrò graficamente in due tavolette andate perdute, raffiguranti rispettivamente il battistero visto dalla porta di Santa Maria del Fiore, la piazza della Signoria e Palazzo Vecchio, ma che sostanzialmente conosciamo grazie alla prima trattazione scritta dell'argomento, il De Pictura (1434-1436), scritto dall'umanista e architetto Leon Battista Alberti, al quale è attribuita da alcuni critici la Prospettiva urbinate.

Le origini dei procedimenti utili a ottenere una corretta rappresentazione prospettica vanno quindi ricercati nell'attività e nella volontà degli artisti. Un risultato ammirevole, di certo fortemente influenzato dalle scoperte del Brunelleschi, e precedente agli scritti dell'Alberti, possiamo vederlo nella famosa Trinità di Masaccio in Santa Maria Novella a Firenze.

Ugualmente importante è l'opera di Melozzo da Forlì, studioso molto rigoroso delle prospettive e degli scorci (come riconosce il Vasari), citato ad esempio da Luca Pacioli, e soprattutto iniziatore di un nuovo tipo di sguardo prospettico: "Fu primo a dipinger le volte con l'arte del sotto in su, la più difficile e la più rigorosa", dice Luigi Lanza.^[5]

Il contributo dell'Alberti fu anche determinante, proprio per la sua forma scritta. Importante fu senz'altro anche la relazione di reciproca stima e di amicizia col Brunelleschi, testimoniata nel "Prologo" della versione in "lingua toscana" del De Pictura, dedicato al più anziano architetto e in cui l'autore chiede all'amico di correggerlo "se cosa vi ti par di emendarla". A quest'opera divisa in tre libri, di cui il primo contiene aspetti matematici, ovvero di ordine geometrico, si può far risalire l'inizio documentato della trattazione scientifica della prospettiva.

Dopo, altri grandissimi artisti del Rinascimento lasciarono scritti sul tema: Piero della Francesca nel De prospectiva pingendi, un trattato in lingua volgare composto nell'ottavo decennio del XV secolo, e Leonardo da Vinci con notazioni e dimostrazioni sparse nei suoi manoscritti (in particolare nel Manoscritto A, datato al 1492 e conservato all'Institut de France di Parigi). È opportuno sottolineare il differente modo di riguardare il problema di Leonardo rispetto agli artisti delle generazioni precedenti. Mentre l'Alberti, considerando le relazioni fra immagine e oggetto reale, pone l'attenzione su rapporti di proporzionalità, Leonardo più sinteticamente mette a fuoco la similitudine, una delle proprietà che sarà fondamentale nello stimolare i successivi sviluppi di ordine teorico, e con la mentalità dello scienziato dice anche: "prospettiva non è altro che sapere bene figurare lo ufizio dell'occhio".^[6]

Rinascimento maturo

In mancanza di sicure basi matematiche, le ricerche sul fenomeno della percezione visiva venivano condotte con semplicissimi strumenti, premesse ai "prospettografi" usati nei secoli successivi, o al massimo con rudimentali camere oscure. Di questi strumenti e del loro uso, oltre alle descrizioni letterarie, abbiamo delle nitide rappresentazioni in alcune notissime incisioni su legno di Albrecht Dürer, inserite come illustrazioni in un suo trattato indirizzato ai giovani artisti, Underweysung der Messung mit dem Zirckel und Richtscheyt (Norimberga, 1525), con testo in tedesco per la prima edizione germanica, poi tradotto in latino con il titolo Institutionum Geometricarum libri quattuor e pubblicato postumo a Parigi nel 1532, con prefazione di Erasmo da Rotterdam.

L'opera è nota anche perché in essa si trovano chiare applicazioni di doppia proiezione ortogonale, fra le prime a essere così sicuramente documentate^[7]. Le xilografie a cui si è fatto cenno mostrano come da una postazione fissa, mirando l'oggetto attraverso un vetro fissato a una cornice o rilevando la posizione di punti della sua proiezione su uno sportello, se ne possa disegnare il perfetto scorcio.

Il Dürer, che aveva compiuto due viaggi in Italia nel 1494 e nel 1505, contribuì fortemente a divulgare le nuove teorie nell'Europa settentrionale soprattutto con la sua immensa opera grafica.

L'interessamento appassionato dei pittori alla prospettiva non era indotto solo dal desiderio di trovare espedienti per giungere a una corretta rappresentazione mimetica del reale. Oltre a conferire all'arte supporti di carattere scientifico, la ricerca era finalizzata a dare evidenza a una concezione filosofica del mondo, basata su un ordine razionale distribuito su tutto il creato. Tale funzione giunse alle sue massime espressioni nel periodo compreso fra la tarda attività di Piero della Francesca e i primi decenni del Cinquecento, prima che il Manierismo si insinuasse a rompere l'equilibrio della precedente visione. Si pensi, ad esempio, all'affresco di Raffaello nella stanza della Segnatura in Vaticano, noto come La scuola di Atene. Quella scena, ambientata nel grandioso spazio definito dalle pilastrate e dalle avvolgenti volte a pieno centro, è un'allegoria dell'universo visibile, come l'affresco posto di fronte nella stessa stanza, la Disputa del Sacramento (o meglio il Trionfo dell'eucaristia) lo è di quello invisibile.

Nei due secoli d'oro del Rinascimento al problema della prospettiva furono quindi interessati quasi esclusivamente gli artisti. Le personalità citate non erano però sprovviste di cognizioni matematiche, e nel caso di Piero della Francesca si ha un vero cultore della materia, tanto da poter essere definito un valente geometra. Essendo in prevalenza pittori, e non potendo oltrepassare ristretti limiti sul piano teorico, dato che gli strumenti matematici a disposizione erano ancora sostanzialmente quelli conosciuti nell'antica età ellenistica, l'aspetto a cui dedicarono le maggiori attenzioni fu l'effetto del digradare dei toni e dei colori in rapporto alla distanza dal punto di osservazione, fino al loro svanire all'orizzonte. Discussero e scrissero molto cioè su quella che viene chiamata la "prospettiva aerea", di origine nordica e veneziana da cui anche Leonardo ha tratto spunto.

Sistemazione teorica

Nella seconda metà del XVI secolo il tema cominciò a interessare studiosi non appartenenti al campo dell'arte, sia in Italia che fuori di essa. E contestualmente si ebbe un secondo salto di qualità, determinato dalla volontà di dare una sistemazione teorica ai procedimenti esecutivi fino ad allora suggeriti. Ciò si può già constatare nell'opera del pesarese Guidobaldo del Monte^[8] e in quella del fiammingo Simon Stevin^[9].

Nel trattato di Guidobaldo del Monte, e più ancora in Ad Vitellionem paralipomena^[10] di Keplero, nella parte dedicata alle coniche, sembra di avvertire la necessità dell'enunciazione di una proposizione che ammetta l'incidenza delle rette parallele. A questo risultato arriverà il lionese Girard Desargues (già autore di un brevissimo trattato sulla prospettiva pubblicato nel 1636^[11]) nel suo Brouillon projet d'une atteinte aux événements des rencontres d'un cône avec un plan^[12], un originalissimo studio sulle coniche in cui, fra l'altro, si risolve proiettivamente il difficile problema di come si possa ottenere un cerchio sezionando con un piano un cono non circolare, non solo ellittico ma anche parabolico o iperbolico, dipendentemente dalla posizione del piano.

Il Desargues, per il Brouillon e per il suo teorema sui triangoli omologici, ha il diritto di essere considerato l'autentico iniziatore della geometria proiettiva. Per l'idea di considerare le rette parallele intersecantisi in un punto all'infinito, egli fu lodato apertamente da Cartesio. Il concetto di punto improprio che implicitamente veniva introdotto apriva la strada alla giustificazione teorica del procedimento costruttivo della prospettiva, permettendo di dare al punto di fuga un'interpretazione puramente geometrico-matematica.

A questo compito, completamente assolto solo fra la fine del Settecento e l'inizio dell'Ottocento, diede un impulso di primaria importanza Brook Taylor con la seconda edizione del suo trattato sulla prospettiva, dal titolo New principles of linear perspective (Londra, 1719). In esso è usata per la prima volta la denominazione "linear perspective" (prospettiva lineare) e sono formulate ineccepibili proposizioni per la determinazione del "vanishing point" di una retta data non parallela al quadro, e della "vanishing line" di un piano dato non parallelo al quadro. Il primo definito come intersezione col quadro di una retta parallela a quella data condotta per l'occhio dell'osservatore, la seconda individuata come intersezione col quadro di un piano parallelo a quello dato passante per lo stesso occhio. Sostituendo il centro di proiezione all'occhio, si ha la descrizione esatta di come ottenere punti e rette di fuga.

Prospettiva "da sotto in su" (a quadro orizzontale vista dal basso)

Le esperienze accumulatesi nell'arco di oltre tre secoli erano tali che nel Settecento non esistevano ormai più segreti su come allestire graficamente una veduta prospettica; fra le molteplici connotazioni e valenze che nel corso della sua storia la prospettiva ha assunto non va certo dimenticato il suo uso a scopo illusionistico. Pur essendo questo un aspetto sempre più o meno insito nelle immagini con essa ottenute, un precipuo interesse per la simulazione è evidenziato da un particolare filone della pittura, quando con essa si vuole annullare la solidità della muratura per aprire illusivamente verso il cielo, ma spesso anche allegoricamente, soffitti e volte. Una prima compiuta e celebre realizzazione di questa tendenza la si ammira nella Camera degli sposi di Andrea Mantegna nel Palazzo Ducale di Mantova, affrescata negli anni a cavallo del 1470.

Ma il maestro ritenuto esemplare per la prospettiva "da sotto in su" è, sempre nel XV secolo, Melozzo da Forlì, coi suoi capolavori a Roma, a Loreto e a Forlì. Passando, dopo di lui, attraverso numerose esperienze, i cui episodi più salienti sono nel Cinquecento la decorazione della cupola e del sottostante tamburo del duomo di Parma a opera del Correggio e nel Seicento l'affresco di Pietro da Cortona sulla volta del salone di Palazzo Barberini a Roma (Trionfo della Divina Provvidenza), si approda all'apice del percorso, nel raggiungimento di effetti che destano meraviglia e stupore, con l'impresa di Andrea Pozzo, fratello laico dell'ordine dei Gesuiti, nella navata centrale della chiesa di Sant'Ignazio a Roma (Gloria di Sant'Ignazio). Si tenga conto che gli affreschi sono dipinti su superfici curve, e per fare in modo che guardandoli dal basso le linee architettoniche e le figure non appaiano deformate, i pittori dovevano ricorrere a espedienti tecnici affini all'anamorfosi, studiati anche sviluppando la superficie curva su cartoni piani, che poi venivano curvati per controllare gli effetti visivi del disegno.

La volontà di dilatare illusivamente l'invaso architettonico verso una spazialità illimitata trovò larga adesione nell'Europa centrale, confortata dal gradimento dei monarchi e degli ordini religiosi committenti. Nei territori tedeschi, austriaci e boemo-moravi fu ostentata da valenti pittori, come Johann Michael Rottmayr, lo svizzero Johann Rudolf Byss, di cui si menziona la decorazione sulla volta dello scalone del castello di Pommersfelden, e Cosmas Damian, quest'ultimo attivo anche come architetto, e spesso operante in simbiosi col fratello Egid Quirin, che si occupava con eccezionale virtuosismo della decorazione plastica a stucco. Di Cosmas Damian, che lasciò una serie di notevoli opere in edifici prevalentemente religiosi, si vuole qui ricordare il limpido e luminoso affresco prospettico nella chiesa abbaziale di Osterhofen (1729-1735), dove è evidente il vivo ricordo del dipinto su tela di Andrea Pozzo rappresentante una finta cupola (1685) e collocato nella chiesa di Sant'Ignazio a Roma, grande tondo che il pittore bavarese aveva visto durante il suo soggiorno romano durato dal 1711 al 1713.

L'influenza del Pozzo nell'Europa centrale, oltre che dal prestigio di cui godeva, fu favorita dalla permanenza a Vienna durante gli ultimi sette anni della sua vita; a divulgare il suo insegnamento contribuì di certo la fama del suo trattato Perspectivae pictorum atque architectorum, illustrato con oltre cento tavole grafiche, pubblicato a Roma nel 1693, quindi ad Augusta nel 1706 e nel 1719, con testo tedesco a fianco di quello latino^[13]. Si noti la Figura 100 dell'opera pubblicata sul Web dalla Universidad de Sevilla (pag.314), in cui sono disegnate le sezioni longitudinale e trasversale di un ambiente architettonico non molto dissimile dal Sant'Ignazio, e in cui sono indicate le posizioni percepite da un osservatore posto al centro della navata, di quanto è effettivamente dislocato sulla superficie della volta; il tutto viene quindi proiettato su una virtuale superficie piana orizzontale situata all'altezza dell'imposta. Proprio la presenza di questo piano nella figura è quanto mai indicativa del procedimento tecnico da seguirsi per il disegno delle composizioni, che sono assimilabili o a prospettive a quadro obliquo dal basso, oppure appaiono come prospettive frontali in cui il piano delle immagini abbia subito una rotazione di 90º per assumere la giacitura orizzontale^[14].

La predilezione per questo tipo di realizzazioni, che avevano anche funzioni celebrative in quanto soddisfacevano l'esigenza dei monarchi di confermare con opere visibili la loro pretesa investitura divina, e parallelamente si prestavano a offrire una sorta di epifania della verità della Chiesa cattolica rispetto a quella protestante, ebbe un trionfale epilogo con l'opera di Giambattista Tiepolo, negli immensi affreschi della residenza del principe vescovo a Würzburg (1751-1753) e del Palazzo reale di Madrid (1762-1766). Accorgimenti tecnici analoghi a quelli adottati per le opere di grandi dimensioni furono adoperati, benché diretti a risultati meno imponenti, da vedutisti e quadraturisti nel secondo Seicento e per tutto il Settecento.

Prospettiva solida

Fra il complesso degli espedienti messi in atto con finalità particolari vanno ricordati anche quelli per realizzare le cosiddette "prospettive solide", in cui l'effetto delle linee si compone con quello del rilievo plastico, fino anche a ottenere spazi che appaiono più profondi di quanto in realtà non siano. Tecnica molto probabilmente già usata nelle scenografie teatrali in età ellenistica e romana, fu ripresa nel Rinascimento e nell'età barocca, e di essa furono dati esempi memorabili, come il coro della chiesa di Santa Maria presso San Satiro in Milano, di Donato Bramante, parti della scena del Teatro Olimpico di Vicenza, realizzate da Vincenzo Scamozzi a completamento del progetto di Andrea Palladio, e la galleria di Palazzo Spada in Roma, di Francesco Borromini. Ora la tecnica è ovviamente studiata nelle scuole di scenografia in quanto rimane un fattore di ricorrente uso nelle scene teatrali.

Nascita della geometria descrittiva

Seguendo l'itinerario storico fin qui percorso, si comprende come la consumata abilità pratica di decoratori e illustratori nel Settecento non avesse ancora un pieno corrispettivo nella consapevolezza teorica del problema. Questa fu però raggiunta di lì a poco. Il grande salto di ordine scientifico e tecnologico maturato nel XVIII secolo richiedeva anche una sistemazione delle scoperte fatte nei secoli precedenti, inducendo a inserirle correttamente nelle diverse branche del sapere, secondo una visione organica di coerenza e di appartenenza. Per quanto riguardava le conoscenze relative a tipi di rappresentazione riconducibili alla geometria, il processo fu senz'altro favorito dalle esigenze che via via si presentavano nel campo della progettazione di beni materiali, per la cui produzione il lavoro artigianale veniva sempre più sostituito dal sistema industriale.

È merito soprattutto della cultura scientifica francese, giunta a un livello altissimo nel secondo Settecento, l'aver dato una risposta adeguata alle varie istanze. Fu infatti Gaspard Monge il primo a ordinare la materia facendone un organismo coordinato di vaste proporzioni, fissando anche in modo preciso i requisiti che un procedimento deve soddisfare per essere considerato un "metodo di rappresentazione". A lui si deve il nome di "geometria descrittiva" e il primo trattato sul tema^[15], raccolta di lezioni che ebbe successive e numerose edizioni, e che si diffuse rapidamente fuori dai confini francesi contribuendo a promuovere le ricerche e gli sviluppi nel campo.

Il metodo noto con il suo nome, benché già usato per alcune particolari applicazioni molto tempo prima, fu da lui teorizzato e divenne il fondamento della geometria descrittiva. L'opera citata non contiene però riferimenti alla prospettiva, che ebbe comunque parte nelle lezioni del suo autore, e fu poi inserita nello stesso corpo della nuova scienza insieme al metodo che ne precisa ogni aspetto teorico, cioè quello della proiezione centrale, elaborato da Jean-Victor Poncelet. La fama e l'importanza di quest'ultimo, già allievo del Monge all'École Polytechnique, è anche e soprattutto dovuta al Traité des propriétés projectives des figures (Parigi, 1822, I edizione), dedicato allo studio delle proprietà delle figure che si conservano inalterate nonostante le trasformazioni che le figure stesse subiscono attraverso operazioni di proiezione e sezione.

Definendo queste come proprietà proiettive e distinguendole dalle altre proprietà geometriche che non lo sono, egli fondò la "geometria proiettiva" come corpo separato dagli altri assetti della geometria. Una separazione poi mantenuta anche in seguito, quando il polo direttivo degli studi, nell'Ottocento inoltrato, si spostò dalla Francia alla Germania. In questo composito contesto la prospettiva, vista in un'ottica che ne rilevi integralmente le connotazioni, si configura come un insieme di elementi capace di raccordare le due branche della geometria fondate dal Monge e dal Poncelet.

Epoca contemporanea

In tempi più recenti sono state proposte concezioni fusioniste miranti a superare le divisioni che possono essere ritenute solo apparenti, concezioni che sono parte di un dibattito di amplissime proporzioni e tendente a ricercare i fondamenti strutturali su cui è costruito l'intero edificio della matematica, con la sua infinita rete di connessioni e articolazioni. Ricerche che però non hanno messo in discussione la teoria fondante ritenuta ancora la più valida, quella degli insiemi. Tutto ciò lascia comunque a margine l'operatore che si avvale tecnicamente di un determinato gruppo di elementi, seppure essi facciano parte di un'immensa costruzione, o addirittura di un universo a sé stante, come è intesa la matematica secondo la concezione neoplatonica di Roger Penrose. I metodi descrittivi di rappresentazione infatti sono ancora quelli definiti nell'Ottocento, con le sole modifiche apportate alle abitudini degli operatori dalla normativa tecnica, al fine di uniformare le convenzioni grafiche per rendere gli elaborati leggibili senza ambiguità alcuna.

Nel campo della pittura, è ovvio che la prospettiva non assolve più ad alcuna funzione da quando gli artisti, almeno quelli più rappresentativi, hanno interrotto con decisione il filo di una continuità che nel passato era durata dalla preistoria fino a quasi tutto l'Ottocento. Le avanguardie del Novecento, dal cubismo in avanti, mirano a espressioni e a effetti che non hanno nulla in comune con le finalità di una prospettiva. Questa invece rimane un validissimo strumento di indagine e di verifica per progettisti, architetti e designer, e per produrre immagini dei beni ideati o costruendi da sottoporre all'attenzione di committenti e potenziali compratori.

Per tali scopi, una risorsa che offre prestazioni sotto vari aspetti enormemente superiori all'esecuzione manuale è quella costituita dagli elaboratori elettronici. Oggi sono disponibili applicazioni software con cui si possono ottenere modelli tridimensionali di qualsiasi oggetto, anche partendo dalle proiezioni ortogonali di esso, come anche si può avere la visualizzazione di ambienti e spazi virtuali del tutto simili a quelli reali. È poi possibile osservare questi modelli da qualsivoglia punto di vista, girando intorno a essi od entrandovi, visualizzando contestualmente innumerevoli prospettive di essi.^[16]

Quanto si è detto ed esposto non vanifica affatto l'importanza di conoscere la struttura geometrico-matematica della prospettiva, la cui validità rimane comunque inalterata come fattore scientifico. Non solo, perché le molteplici possibilità offerte dai programmi informatici, lungi dal diminuirla, ne potenziano la validità come strumento di verifica e di indagine, al di là del fatto che una vista prospettica sia ottenuta dall'elaboratore elettronico o manualmente. Inoltre, nelle fasi di ideazione e progettazione di beni materiali riconducibili alle costruzioni, di qualunque genere esse siano, il lavoro grafico manuale rimane spesso un passaggio ineludibile.

Rappresentazione prospettica

Gli elementi fondamentali necessari alla costruzione della prospettiva di una figura obiettiva, che si suppone data nello spazio, sono, come per ogni metodo di rappresentazione, il piano di proiezione, a cui si dà in genere il nome specifico di "quadro prospettico", e il centro di proiezione, chiamato normalmente "punto di vista" o "centro di vista". Per procedere operativamente nel disegno occorre anche fissare la posizione di alcuni elementi di riferimento, di seguito elencati. Un piano orizzontale, detto "piano di terra" o "piano geometrale", che intersecando il quadro fornisce la "linea di terra", luogo delle tracce di tutte le rette appartenenti allo stesso piano geometrale. La proiezione ortogonale del punto di vista sul piano geometrale individua il cosiddetto "punto di stazionamento", mentre la proiezione ortogonale dello stesso punto di vista sul quadro determina il "punto principale". L'intersezione del quadro con un piano orizzontale passante per il punto di vista è una retta denominata "linea d'orizzonte", parallela alla linea di terra e luogo delle fughe di tutte le rette orizzontali, ovvero retta di fuga di tutti i piani paralleli a quello geometrale. In alcuni casi può essere utile tracciare il "cerchio di distanza", che ha il centro nel punto principale, raggio uguale alla distanza del punto di vista dal quadro, ed è il luogo geometrico delle fughe di tutte le rette inclinate di 45° rispetto al quadro. È inoltre necessario disporre delle proiezioni ortogonali della figura obiettiva, la cui vista dall'alto, o pianta, viene di solito riportata sul piano di terra.

Occorre ancora tenere presente che la sintesi teorica della prospettiva va ricercata nel "metodo della proiezione centrale", o di Poncelet. Ma mentre questo si occupa della rappresentazione degli enti e degli elementi geometrici considerati nella loro astrattezza, e di dare corrette soluzioni dei problemi inerenti alle relazioni fra gli enti stessi, come l'appartenenza, il parallelismo, l'ortogonalità, il fine della prospettiva è di fornire immagini realistiche delle strutture oggettuali proiettate. In essa, la determinazione delle immagini degli enti geometrici fondamentali è comunque basata sulle loro proprietà, e sulla struttura tipica del metodo della proiezione centrale. Quindi per la retta, essendo essa individuata da due punti, occorre disporre della proiezione di questi per potere tracciare la sua immagine. I due punti più notevoli di detta immagine sono la traccia della retta, punto della sua intersezione col quadro, e la fuga della retta, proiezione sul quadro del suo punto improprio, che perciò si ottiene come intersezione col quadro della parallela alla retta condotta per il centro di vista. Ancora, l'immagine di un punto deve essere determinata come intersezione delle immagini di due rette passanti per esso. Infine, un piano è individuato dalla sua traccia, retta d'intersezione del piano stesso col quadro, e dalla sua fuga, proiezione sul quadro della sua retta all'infinito.

Operativamente, si può procedere o con due fogli separati (sistema indiretto), o con un unico foglio (sistema diretto). Nel primo caso un foglio conterrà la proiezione ortogonale degli elementi riportati sul piano di terra, e l'altro corrisponderà al quadro; nel secondo caso normalmente si dispone nella parte inferiore del foglio la vista dall'alto del piano di terra, e nella parte superiore il quadro a partire dalla linea di terra.

Nei confronti della figura obiettiva, il quadro può assumere infinite posizioni, come anche infinite inclinazioni rispetto al piano geometrale. Se ad esempio, fissato il centro di vista, il quadro si sposta rispetto alla figura obiettiva conservando la medesima giacitura, si otterranno, in corrispondenza delle diverse posizioni, delle immagini simili fra loro che sono casi di omotetia. Se invece si considerano le possibili e diverse inclinazioni del quadro, ovvero le sue variazioni di giacitura, si perviene alla determinazione dei tipi di prospettiva classificati dalla normativa tecnica, che sono la "prospettiva frontale" (o centrale) e la "prospettiva accidentale" quando il quadro è verticale, e la "prospettiva razionale" quando il quadro è inclinato.

Esempio di una prospettiva frontale (o centrale)

Esempio di una prospettiva d'angolo (o accidentale)

Esempio di una prospettiva d'angolo a quadro verticale di una composizione di parallelepipedi

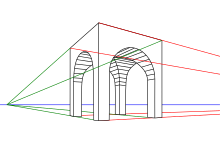
Per definire le caratteristiche fondamentali dei tre tipi di prospettiva sopra elencati, conviene riferire la figura obiettiva a una terna di assi cartesiani coordinati, due dei quali siano paralleli al piano geometrale e il terzo, di conseguenza, normale a esso. Per semplicità si pensi a un cubo o ad un parallelepipedo con tre spigoli concorrenti in uno stesso vertice, rispettivamente giacenti su ciascuno dei tre assi cartesiani, quindi con quel vertice coincidente con l'origine degli assi. Disponendo il quadro parallelo a due degli assi cartesiani, e prescindendo dall'aggiunta di rette ausiliarie necessarie alla costruzione dell'immagine, con gli elementi dello schema preso in esame è possibile individuare soltanto un punto di fuga proprio (quello delle rette con direzione normale al quadro, che è il punto principale). Si ha in questo caso la prospettiva di fronte (detta anche, tradizionalmente, "prospettiva centrale", terminologia dovuta alla posizione più frequentemente assegnata al punto principale nelle opere degli artisti rinascimentali. Tale denominazione non deve generare confusione con la dizione relativa alle caratteristiche generali del sistema, che si avvale dei principi delle proiezioni centrali). Se il quadro è invece parallelo a un solo asse cartesiano, e di conseguenza obliquo agli altri due, con gli elementi dello schema si individuano due punti di fuga propri. Si configura in questo secondo caso la prospettiva accidentale (detta anche d'angolo). Se infine il quadro è obliquo a tutti tre gli assi cartesiani, si hanno tre punti di fuga propri e il caso più generale della prospettiva razionale (o a quadro inclinato).

Un'immagine prospettica, essendo improntata a caratteri di verosimiglianza, deve essere in grado di soddisfare esigenze di gradevolezza visiva, deve cioè corrispondere, per quanto possibile, al tipo di visione percepito dall'essere umano. Una perfetta corrispondenza fra immagini piane e quelle proiettate sul fondo dell'occhio non è però possibile, essendo le seconde distribuite su una superficie curva, ma si ottiene un'accettabile limitazione delle difformità assegnando al cosiddetto "cono visivo" un angolo di apertura opportuno. Detto cono ha vertice nel centro di vista e dovrebbe contenere tutti i raggi proiettanti passanti per gli infiniti punti della figura obiettiva; la sua intersezione col quadro è un cerchio (da non confondersi col cerchio di distanza) con centro nel punto principale, e il suo angolo di apertura non deve superare di norma i 60°. Il cerchio così ottenuto costituisce un limite di notevole importanza, poiché all'interno di esso la rappresentazione conserva requisiti di accettabilità, e sono evitate macroscopiche "aberrazioni" nelle immagini, così che queste appaiono assimilabili a quelle incluse nel campo visivo umano. La normativa tecnica è particolarmente restrittiva, prescrive infatti per l'angolo di apertura del cono visivo un'ampiezza massima di 35°.

Metodi esecutivi

Una suddivisione in differenti sistemi o metodi del complesso di operazioni finalizzate alla costruzione di prospettive, è del tutto convenzionale, in quanto i criteri per ottenere le immagini degli enti geometrici fondamentali sono sempre quelli indicati nel paragrafo precedente, qualunque sia il metodo seguito. La classificazione è comunque utile, ed è infatti adottata anche dalla normativa tecnica, per indicare diverse modalità di procedere onde determinare la prospettiva della pianta (o vista dall'alto) della struttura oggetto dell'operazione, soprattutto in riferimento alla scelta delle rette utili alla determinazione dei punti notevoli della struttura. Tale scelta è legata a fattori di economia grafica; inoltre, non sempre si procede utilizzando un solo metodo, ma in uno stesso disegno spesso si individuano gli elementi utili nella maniera che risulta più conveniente od immediata.

Per costruire l'immagine prospettica di una struttura oggettuale, si comincia normalmente col disegnare la prospettiva della sua vista dall'alto (o pianta), vista che è data secondo il metodo delle proiezioni ortogonali (o di Monge). Solo in alcuni casi di prospettiva a quadro obliquo, può essere conveniente iniziare da livelli differenti.

La descrizione seguente si consideri quindi riferita ai soli casi di quadro verticale. La pianta viene di solito riportata direttamente sul piano geometrale. Però, qualora il punto di vista fosse molto basso, e di conseguenza l'orizzonte vicino alla linea di terra, determinando un'immagine del geometrale molto schiacciata, onde ottenere risultati precisi si può disegnare la prospettiva della pianta prima su un piano virtuale collocato più in basso, per poi riportare la posizione dei punti nella loro giusta collocazione al disopra della linea di terra. Completata questa prima fase, occorre determinare l'immagine dei punti della struttura nella loro effettiva configurazione spaziale. A tale scopo è necessario conoscerne le reali quote (cioè le loro altezze sul piano geometrale), rilevabili da prospetti e sezioni anch'esse date mediante il metodo del Monge.

Le operazioni da eseguire sono assai semplici, perché nella prospettiva frontale e in quella accidentale la fuga delle rette verticali è un punto improprio, e quindi le immagini di tali rette rimangono verticali. Basta quindi riportare sul quadro, in posizione opportuna, le quote reali nella scala assegnata al disegno, per poi determinare, sempre attraverso le intersezioni delle immagini prospettiche di due rette per ciascuno dei punti, le proiezioni effettive di essi nello spazio. La fuga di una retta non orizzontale, ovviamente non sta sull'orizzonte. Qualora sia necessario individuarla, occorre disegnare sul quadro il ribaltamento del raggio proiettante parallelo alla retta, ribaltamento che si immagina avvenire intorno al punto di fuga cercato ed è rappresentato da una linea inclinata sull'orizzonte di un angolo uguale a quello di pendenza della retta nello spazio; l'intersezione fra il raggio ribaltato e la verticale condotta per la fuga della proiezione orizzontale della retta, fornisce il punto cercato. I disegni riportati in questa sezione illustrano chiaramente i procedimenti fin qui e di seguito descritti.

Metodo dei punti di distanza

Fra i vari procedimenti esecutivi dotati di caratteristiche particolari, e tali da poter essere definiti, seppur convenzionalmente, dei metodi, il primo a essere adoperato fu quello dei punti di distanza. Esso è infatti il sistema impiegato dai maestri toscani del primo Quattrocento, ma anche da artisti come Mantegna e Melozzo da Forlì, ed usato costantemente fino al Cinquecento inoltrato. Si è già definito in "Generalità" il cerchio di distanza, che può anche essere riguardato come il luogo di tutti i possibili ribaltamenti sul quadro del centro di vista. Dai pittori venivano sfruttati i due punti della sua intersezione con l'orizzonte, fughe delle rette orizzontali inclinate di 45º rispetto al quadro. Queste due direzioni, essendo le stesse delle diagonali di quadrati giacenti sul piano geometrale e con i lati rispettivamente ortogonali e paralleli al quadro, permettevano di determinare in modo facile e rapido la prospettiva dei pavimenti, da cui i pittori partivano per poi completare l'ambientazione architettonica del dipinto. Il procedimento è conveniente e ancora applicato per l'esecuzione manuale delle prospettive frontali.

Il disegno riportato a lato rappresenta la prospettiva di un solido ottenuto da un originario esaedro, tagliando di sguincio tutti i suoi dodici spigoli. I due punti di fuga sull'orizzonte sono il punto principale a destra e un punto di distanza a sinistra. L'immagine prospettica è costruita secondo i criteri già descritti. Si richiama l'attenzione sulla figura disegnata al disotto della linea di terra, che è una vista dall'alto del solido appartenente al piano geometrale e ribaltata, con una rotazione di 90º, sullo stesso quadro. Non ci si lasci quindi confondere dall'apparente direzione delle rette inclinate di 45º rispetto alla linea di terra. La loro reale posizione nello spazio richiede per esse, quale punto di fuga, il punto di distanza fissato a sinistra sull'orizzonte.

Metodo del taglio

Anche il metodo chiamato del taglio si può far risalire all'originaria concezione dell'Alberti di considerare la "pittura non altro che intersegazione della pirramide visiva, secondo data distanza, posto il centro e constituiti i lumi, ...." (Della pittura, Libro I, 12; dove "pittura" è intesa chiaramente in un'accezione più tecnica che artistica). La sua sistemazione fu però completata nei secoli successivi al quindicesimo. Non è un procedimento molto pratico per l'esecuzione manuale, perché i punti utili a costruire l'immagine, al fine di conservare la precisione nel disegno, debbono essere riportati direttamente dalle intersezioni dei raggi proiettanti col quadro, individuate sulla vista dall'alto e su quella di profilo, e qualora sia necessario anche su una vista dal basso. Ciò comporta la necessità di avere molti grafici in un unico foglio, con la conseguenza di ottenere una prospettiva relativamente piccola rispetto all'estensione del campo su cui si opera.

Metodo dei punti di fuga

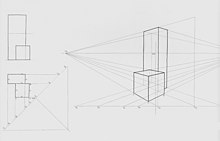
Anche il metodo dei punti di fuga fu elaborato da artisti del passato prima di ricevere una sistemazione teorica nella visione organica del Poncelet. Lo si vede applicato in modo piuttosto corretto ad esempio in noti disegni e incisioni del bolognese Ferdinando Galli da Bibbiena (1657-1743), architetto e scenografo che già in vita godette di fama europea (Vedi collegamento esterno). Nella sua struttura sistemica, per la rappresentazione del punto il metodo fa ricorso a due rette fra loro perpendicolari, in modo che la fuga di ciascuna sia l'antipolare, rispetto al cerchio di distanza, della fuga del piano a essa ortogonale e passante per l'altra. Si esprime la condizione anche dicendo che le fughe delle due rette sono punti anticoniugati rispetto al cerchio di distanza. Non ci si sofferma qui sull'illustrazione di questa proprietà, che esula dai limiti della presente trattazione, e per la quale si rimanda allo studio del citato "metodo della proiezione centrale". Dal punto di vista operativo il procedimento è applicabile per strutture oggettuali in cui prevalgano spigoli orientati secondo due direzioni ortogonali fra loro, come accade in molti edifici di tipo tradizionale. Presenta l'inconveniente che le tracce delle rette condotte per punti viepiù lontani dal quadro, risultano notevolmente distanti dalla linea mediana del disegno, e molte di esse possono trovarsi all'esterno del foglio.

Metodo dei punti misuratori

Per rendere più agevoli le operazioni grafiche, si ricorre frequentemente al metodo dei punti misuratori, l'ultimo in ordine di tempo a essere stato introdotto. In esso anziché ricorrere, per la rappresentazione del punto, a due rette fra loro ortogonali, si sceglie una prima retta in funzione della direzione più conveniente ai fini dell'economia grafica, e la seconda viene individuata dalla corda dell'arco di ribaltamento del punto sul quadro, facendo ruotare la prima intorno alla sua traccia, come risulta chiaramente dal disegno sopra riprodotto. Le fughe delle rette su cui si trovano le corde dei diversi archi di ribaltamento (due per le strutture caratterizzate da profili tutti ortogonali fra loro), si chiamano "punti misuratori" in quanto consentono di "misurare" la scansione delle distanze nell'immagine prospettica. Detto questo, si riconosce come anche i punti di distanza sull'orizzonte siano due particolari misuratori, fughe delle corde degli archi descritti da punti appartenenti a rette normali al quadro, quando queste vengono ribaltate. È questo un ulteriore elemento per capire come la suddivisione del procedimento costruttivo della prospettiva in diversi sistemi o metodi, sia un fatto puramente convenzionale, legato soprattutto all'evoluzione storica delle applicazioni.

Casi non ortogonali al piano di terra

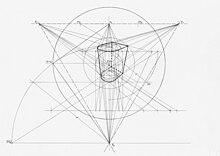
Fin qui si sono esposte le operazioni da eseguire col presupposto di riferirsi a prospettive a quadro verticale. Qualora il quadro non sia ortogonale al piano di terra, si hanno i due casi di prospettiva a quadro obliquo dal basso e a quadro obliquo dall'alto. L'adozione di un piano inclinato per l'immagine, dipende dalle caratteristiche della figura obiettiva e dagli effetti che si vogliono ottenere. È quindi plausibile per strutture con grande sviluppo verticale e per la rappresentazione di vaste aree edificate, per le quali si adotta la vista da punti elevati, detta anche "a volo d'uccello". I principi generali attinenti alla rappresentazione degli enti geometrici fondamentali non mutano rispetto a quanto si è già detto, ma le costruzioni grafiche risultano decisamente più complesse di quelle che si eseguono per la prospettiva frontale e per quella accidentale. Nel caso generale di quadro obliquo ai tre assi cartesiani coordinati ai quali può essere riferita la figura obiettiva, si hanno, per le rette rispettivamente parallele ai tre suddetti assi, tre punti di fuga propri che sono vertici di un triangolo di cui il punto principale costituisce l'ortocentro.

Le ultime due figure sono esemplificative delle operazioni relative all'esecuzione manuale di una prospettiva a quadro obliquo. Nel disegno con la rappresentazione mongiana del solido oggetto dell'esercizio, è stato necessario eseguire il ribaltamento (equivalente a una terza proiezione) per determinare la posizione di tutti gli elementi utili. Il cerchio di distanza nella prospettiva è stato tracciato per metterne in evidenza la relazione con gli altri elementi, ma non è strettamente necessario in questo particolare caso, mentre quello più piccolo concentrico a esso è l'intersezione col quadro del cono visivo, all'interno del quale l'immagine non subisce aberrazioni fastidiose. Il disegno di una prospettiva richiede notevole precisione grafica, gli errori infatti si trasmettono da un'operazione all'altra anche ampliandosi. Per questo la posizione di alcuni punti è stata determinata incrociando fra loro i risultati di almeno due operazioni; le altezze delle due ellissi, immagini prospettiche dei cerchi individuati sulle due basi del solido, sono state verificate anche col metodo del taglio, che è possibile applicare al ribaltamento nella prima figura. Si nota come in complesso una prospettiva a quadro obliquo sia notevolmente più laboriosa di una a quadro verticale della stessa struttura oggettuale.

In riferimento all'uso dell'elaboratore elettronico, va da sé che l'analisi della struttura dei software adatti a visualizzare le prospettive di una singola figura obiettiva o di un loro insieme, esula completamente dai limiti della presente trattazione. Ciò non solo perché i programmi sono venduti a costi elevati e la loro struttura non è resa pubblica, o almeno non è completamente leggibile, ma anche perché tale analisi avrebbe significato solo se rapportata al metodo con cui l'elaboratore esegue le informazioni ricevute dal programma, in merito al loro trattamento.

Metodo del ribaltamento omologico (unificazione dei metodi storici)

I metodi di rappresentazione prospettica di cui sopra sono stati elaborati a volte empiricamente, anche se scientificamente corretti, prima di Poncelet, e non potevano, quindi, essere trattati con l'omologia, messa a punto dal Poncelet stesso nel suo trattato del 1822. Da allora, a seguito della definizione di prospettività, e di doppia prospettività in particolare, sarebbe stato logico aspettarsi che scomparissero dalla didattica della prospettiva, o vi prendessero parte solo come interesse storico.

In effetti, se sul quadro (piano di proiezione) si ribalta il piano di terra (possibilmente con la parte più lontana dall'osservatore ruotata nella parte superiore del quadro stesso) si vengono a trovate su di esso due figure, una quella ribaltata, e l'altra costituita dalla prospettiva della figura sul piano di terra. Quella prospettica, come noto, è la sezione della piramide visiva con centro nel punto di vista (occhio dell'osservatore), mentre quella ribaltata è la sezione di una proiezione cilindrica (o parallela) eseguita da un centro di proiezione improprio ortogonale al piano bisettore del diedro formato dai due piani in questione, e cioè il piano di terra e il quadro.

Poiché le due figure sul quadro sono state ottenute da due centri di proiezione differenti, tra loro intercorre una relazione di omologia, per cui punti omologhi sono allineati con il centro di omologia (costituito dall'intersezione della congiungente i due centri di proiezione sul quadro), e rette omologhe si incontrano sull'asse di omologia (costituito dalla retta comune ai due piani). Con queste considerazioni perde importanza la caratterizzazione metrica di parallelismo, ed è possibile usare un'unica metodologia esecutiva per i tre tipi di prospettiva (centrale, accidentale e razionale o a quadro inclinato).

Restituzione prospettica

È il metodo opposto alla proiezione prospettica. Grazie a questo metodo da una prospettiva già realizzata si ricava la pianta ed eventualmente l'alzato in vera forma.

Note

^ a condizione che l'obiettivo della macchina fotografica non provochi distorsioni evidenti (nell'immagine riprodotta, una lieve distorsione è riscontrabile sulla sinistra)
^ Giacomo Devoto, Gian Carlo Oli, Vocabolario illustrato della lingua italiana, Selezione dal Reader's Digest, Milano.
^ De Vecchi-Cerchiari, cit., pag. 27.
^ Brunelleschi, Giunti 2003, p. 10.
^ L. Lanza, Storia pittorica della Italia, Piazzini, Firenze 1834, p. 32.
^ Manoscritto A, foglio 3, recto
^ vedi collegamento esterno.
^ Guidi Ubaldi e Marchionibus Montis, Perspectivae libri sex, Pisauri, 1600
^ Simon Stewin, Livre de l'optique, V, pubblicato postumo a Leida in Oeuvres, tradotto in francese, nel 1634
^ Francoforte, 1604
^ Méthode universelle de mettre en perspective les objets donnés réellement, Parigi, 1636, poco più che un opuscolo, essendo composto di 12 pagine e contenente un solo esempio applicativo.
^ Parigi, 1639
^ Vedi collegamento esterno.
^ Vedere quanto esposto di seguito in "#Generalità e in "#Metodi esecutivi"
^ Géométrie Descriptive, leçons données aux Ecoles Normales l'an 3 de la République, 1ª ed., Paris, an VII (1798)
^ Vedi il collegamento esterno a "Great Buildings Collection", un portale sull'architettura da dove si può scaricare gratuitamente la versione semplificata di un programma che consente di osservare da ogni posizione vari modelli schematici di celebri edifici. Basta anche fare alcune prove con Google Earth per rendersi conto delle risorse offerte dai sistemi elettronici integrati.

Bibliografia

L. Berzolari, G. Vivanti, D. Gigli (a cura di), Enciclopedia delle matematiche elementari e complementi, Volume II - Parte 2º, Ristampa anastatica, Ulrico Hoepli Editore, Milano, 1979 (L'opera è anche una preziosa fonte di minuziosa informazione bibliografica)
Carl B. Boyer, Storia della matematica, Mondadori, Milano, 1980
Anna Maria Brizio (a cura di), Leonardo da Vinci, Pensieri sull'Universo, UTET, Torino, 1952
Dante Nannoni, Il mondo delle proiezioni, applicazioni della geometria descrittiva e proiettiva, Volume 1, 2, 3, Cappelli editore, Bologna, 1975
Giuseppe Pacciarotti, La pittura del Seicento, Utet, Torino, 1997
Roger Penrose, La strada che porta alla realtà, Le leggi fondamentali dell'universo, BUR Scienza, Milano, 2006
Grigore Arbore Popescu, L'arte nell'età delle monarchie assolute, UTET, Torino, 1997
Paolo Rossi (diretta da), Storia della scienza, Volume 1, 2 (tomo 1º e 2º), 3 (tomo 1º e 2º), Utet, Torino, 1988
Pierluigi De Vecchi ed Elda Cerchiari, I tempi dell'arte, volume 2, Bompiani, Milano 1999. ISBN 88-451-7212-0

Voci correlate

Altri progetti

Wikiquote contiene citazioni sulla prospettiva
Wikizionario contiene il lemma di dizionario «prospettiva»
Wikimedia Commons contiene immagini o altri file sulla prospettiva

Collegamenti esterni

(EN) Eric W. Weisstein, Prospettiva, su MathWorld, Wolfram Research.
handprint: elements of perspective, su handprint.com. URL consultato il 20 febbraio 2022.
Underweysung der Messung mit dem Zirckel und Richtscheyt, su digital.slub-dresden.de. URL consultato il 28 febbraio 2009 (archiviato dall'url originale il 1º giugno 2009).
Perspective menu, su fulltable.com.
Trattato di Galli da Bibiena, su unav.es.
Perspectivae Pictorum atque Architectorum, su fondosdigitales.us.es.
I prospettografi: dalla storia alla scuola (PDF), su galileo.cincom.unical.it. URL consultato il 28 luglio 2019 (archiviato dall'url originale il 13 novembre 2012).
Le sezioni coniche (DOC), su dm.uniba.it. URL consultato il 19 febbraio 2009 (archiviato dall'url originale il 2 novembre 2012).

Controllo di autorità	Thesaurus BNCF 8736

Portale Arte

Portale Fotografia

[1] zione che l'obiettivo della macchina fotografica non provochi distorsioni evidenti (nell'immagine riprodotta, una lieve distorsione è riscontrabile sulla sinistra)

[2] Giacomo Devoto, Gian Carlo Oli, Vocabolario illustrato della lingua italiana, Selezione dal Reader's Digest, Milano.

[3] De Vecchi-Cerchiari, cit., pag. 27.

[4] Brunelleschi, Giunti 2003, p. 10.

[5] L. Lanza, Storia pittorica della Italia, Piazzini, Firenze 1834, p. 32.

[6] Manoscritto A, foglio 3, recto

[7] vedi collegamento esterno.

[8] Guidi Ubaldi e Marchionibus Montis, Perspectivae libri sex, Pisauri, 1600

[9] Simon Stewin, Livre de l'optique, V, pubblicato postumo a Leida in Oeuvres, tradotto in francese, nel 1634

[10] Francoforte, 1604

[11] Méthode universelle de mettre en perspective les objets donnés réellement, Parigi, 1636, poco più che un opuscolo, essendo composto di 12 pagine e contenente un solo esempio applicativo.

[12] Parigi, 1639

[13] Vedi collegamento esterno.

[14] Vedere quanto esposto di seguito in "#Generalità e in "#Metodi esecutivi"

[15] Géométrie Descriptive, leçons données aux Ecoles Normales l'an 3 de la République, 1ª ed., Paris, an VII (1798)

[16] Vedi il collegamento esterno a "Great Buildings Collection", un portale sull'architettura da dove si può scaricare gratuitamente la versione semplificata di un programma che consente di osservare da ogni posizione vari modelli schematici di celebri edifici. Basta anche fare alcune prove con Google Earth per rendersi conto delle risorse offerte dai sistemi elettronici integrati.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

Prospettiva

Indice

Etimologia