Funzione zeta di Hurwitz

In matematica, in particolare in teoria analitica dei numeri, la funzione zeta di Hurwitz è una funzione zeta che deve il suo nome al matematico tedesco Adolf Hurwitz. La funzione è definita attraverso la serie

$\zeta (s,q)=\sum _{n=0}^{\infty }{\frac {1}{(q+n)^{s}}},$

se $\operatorname {Re} (s)>1$ e $\operatorname {Re} (q)>0$. Chiaramente, se $q=1$ la funzione zeta di Hurwitz coincide con la funzione zeta di Riemann, cioè $\zeta (s,1)=\zeta (s)$.

Allo stesso modo della funzione zeta di Riemann, $\zeta (s,q)$ può essere prolungata analiticamente a una funzione olomorfa sull'intero piano complesso, ad eccezione di $s=1$.

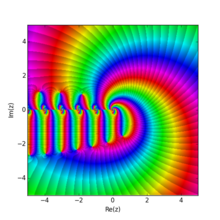
Funzione zeta di Hurwitz con $q=1/3$. Il grafico è stato fatto con matplotlib utilizzando una versione del metodo della colorazione del dominio.

Prolungamento analitico

Funzione zeta di Hurwitz con $q=24/25$ .

Se $\mathrm {Re} (s)\leq 1$, si può definire la funzione per mezzo della seguente equazione

$\zeta (s,q)=\Gamma (1-s){\frac {1}{2\pi i}}\int _{C}{\frac {z^{s-1}e^{qz}}{1-e^{z}}}dz$

dove il contorno $C$ è una linea chiusa attorno all'asse reale negativo.

Si può essere quindi prolungare analiticamente a una funzione meromorfa, con il punto $s=1$ come unico polo semplice e di residuo $1$. Il termine costante è dato da

$\lim _{s\to 1}\left[\zeta (s,q)-{\frac {1}{s-1}}\right]={\frac {-\Gamma '(q)}{\Gamma (q)}}=-\psi (q)$

dove $\Gamma$ è la funzione Gamma e $\psi$ la funzione digamma.

Rappresentazioni

Rappresentazione in serie

Funzione zeta di Hurwitz con parametro $q$ e $s=3+4i$.

Nel 1930, Helmut Hasse fornì una rappresentazione in serie di Newton convergente definita per $q>0$ reale e $s\neq 1$:

$\zeta (s,q)={\frac {1}{s-1}}\sum _{n=0}^{\infty }{\frac {1}{n+1}}\sum _{k=0}^{n}(-1)^{k}{n \choose k}(q+k)^{1-s}.$

Questa serie converge uniformemente in ogni sottoinsieme compatto del semipiano di $s$ a una funzione intera. SI comprende che la somma interna è la $n$-esima differenza in avanti di $q^{1-s}$, cioè

$\Delta ^{n}q^{1-s}=\sum _{k=0}^{n}(-1)^{n-k}{n \choose k}(q+k)^{1-s}$

dove $\Delta$ è l'operatore di differenza in avanti. Quindi, si può scrivere

${\begin{aligned}\zeta (s,q)&={\frac {1}{s-1}}\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{n+1}}\Delta ^{n}q^{1-s}\\&={\frac {1}{s-1}}{\log(1+\Delta ) \over \Delta }q^{1-s}\end{aligned}}$

Altre serie globalmente convergenti sono le seguenti

$\zeta (s,v-1)={\frac {1}{s-1}}\sum _{n=0}^{\infty }H_{n+1}\sum _{k=0}^{n}(-1)^{k}{\binom {n}{k}}(k+v)^{1-s}$

$\zeta (s,v)={\frac {k!}{(s-k)_{k}}}\sum _{n=0}^{\infty }{\frac {1}{(n+k)!}}\left[{n+k \atop n}\right]\sum _{l=0}^{n+k-1}\!(-1)^{l}{\binom {n+k-1}{l}}(l+v)^{k-s},\quad k=1,2,3,\ldots$

$\zeta (s,v)={\frac {v^{1-s}}{s-1}}+\sum _{n=0}^{\infty }|G_{n+1}|\sum _{k=0}^{n}(-1)^{k}{\binom {n}{k}}(k+v)^{-s}$

$\zeta (s,v)={\frac {(v-1)^{1-s}}{s-1}}-\sum _{n=0}^{\infty }C_{n+1}\sum _{k=0}^{n}(-1)^{k}{\binom {n}{k}}(k+v)^{-s}$

$\zeta (s,v){\big (}v-{\tfrac {1}{2}}{\big )}={\frac {s-2}{s-1}}\zeta (s-1,v)+\sum _{n=0}^{\infty }(-1)^{n}G_{n+2}\sum _{k=0}^{n}(-1)^{k}{\binom {n}{k}}(k+v)^{-s}$

$\zeta (s,v)=-\sum _{l=1}^{k-1}{\frac {(k-l+1)_{l}}{(s-l)_{l}}}\zeta (s-l,v)+\sum _{l=1}^{k}{\frac {(k-l+1)_{l}}{(s-l)_{l}}}v^{l-s}+k\sum _{n=0}^{\infty }(-1)^{n}G_{n+1}^{(k)}\sum _{k=0}^{n}(-1)^{k}{\binom {n}{k}}(k+v)^{-s}$

dove $H_{n}$ sono i numeri armonici, $\left[{\cdot \atop \cdot }\right]$ sono i numeri di Stirling del primo tipo, $(\ldots )_{\ldots }$ è il simbolo di Pochhammer, $G_{n}$ sono i coefficienti di Gregory, $G_{n}^{(k)}$ sono i coefficienti di Gregory di ordine superiore e $C_{n}$ sono i numeri di Cauchy del secondo tipo ($C_{1}=1/2$, $C_{2}=5/12$, $C_{3}=3/8$,...), vedere l'articolo di Blagouchine.

Rappresentazione integrale

La funzione ha una rappresentazione integrale in termine della trasformata di Mellin,

$\zeta (s,q)={\frac {1}{\Gamma (s)}}\int _{0}^{\infty }{\frac {t^{s-1}e^{-qt}}{1-e^{-t}}}dt$

per $\mathrm {Re} (s)>1$ e $\mathrm {Re} (q)>0.$

Proprietà

Formula di Hurwitz

La formula di Hurwitz afferma che

$\zeta (1-s,x)={\frac {1}{2s}}\left[e^{-i\pi s/2}\beta (x;s)+e^{i\pi s/2}\beta (1-x;s)\right]$

dove

$\beta (x;s)=2\Gamma (s+1)\sum _{n=1}^{\infty }{\frac {\exp(2\pi inx)}{(2\pi n)^{s}}}={\frac {2\Gamma (s+1)}{(2\pi )^{s}}}{\mbox{Li}}_{s}(e^{2\pi ix})$

è la rappresentazione della funzione valida per $0\leq x\leq 1$ e $s>1$, e inoltre ${\text{Li}}_{s}(z)$ indica il polilogaritmo.

Equazione funzionale

L'equazione funzionale mette in relazioni i valori della funzione di Hurwitz sulla parte destra e sinistra del piano complesso. Per $1\leq m\leq n$ interi, per ogni valore di $s$ si ha

$\zeta \left(1-s,{\frac {m}{n}}\right)={\frac {2\Gamma (s)}{(2\pi n)^{s}}}\sum _{k=1}^{n}\left[\cos \left({\frac {\pi s}{2}}-{\frac {2\pi km}{n}}\right)\;\zeta \left(s,{\frac {k}{n}}\right)\right].$

Alcune somme finite

Le seguenti somme finite sono strettamente collegate all'equazione funzionale, alcune delle quali possono essere valutate in forma chiusa

$\sum _{r=1}^{m-1}\zeta \left(s,{\frac {r}{m}}\right)\cos {\dfrac {2\pi rk}{m}}={\frac {m\Gamma (1-s)}{(2\pi m)^{1-s}}}\sin {\frac {\pi s}{2}}\cdot \left\{\zeta \left(1-s,{\frac {k}{m}}\right)+\zeta \left(1-s,1-{\frac {k}{m}}\right)\right\}-\zeta (s)$

$\sum _{r=1}^{m-1}\zeta \left(s,{\frac {r}{m}}\right)\sin {\dfrac {2\pi rk}{m}}={\frac {m\Gamma (1-s)}{(2\pi m)^{1-s}}}\cos {\frac {\pi s}{2}}\cdot \left\{\zeta \left(1-s,{\frac {k}{m}}\right)-\zeta \left(1-s,1-{\frac {k}{m}}\right)\right\}$

$\sum _{r=1}^{m-1}\zeta ^{2}\left(s,{\frac {r}{m}}\right)={\big (}m^{2s-1}-1{\big )}\zeta ^{2}(s)+{\frac {2m\Gamma ^{2}(1-s)}{(2\pi m)^{2-2s}}}\sum _{l=1}^{m-1}\left\{\zeta \left(1-s,{\frac {l}{m}}\right)-\cos \pi s\cdot \zeta \left(1-s,1-{\frac {l}{m}}\right)\right\}\zeta \left(1-s,{\frac {l}{m}}\right)$

dove $m$ è un intero positivo maggiore di $2$ e $s$ è un numero complesso..

Trasformata di Fourier

La trasformata discreta di Fourier della funzione zeta di Hurwitz rispetto all'ordine $s$ è la funzione chi di Legendre.

Valori razionali

La funzione zeta di Hurwitz calcolata nei numeri razionali compare in molte identità impressionanti. In particolare, in termini dei polinomi di Eulero $E_{n}(x)$:

$E_{2n-1}\left({\frac {p}{q}}\right)=(-1)^{n}{\frac {4(2n-1)!}{(2\pi q)^{2n}}}\sum _{k=1}^{q}\zeta \left(2n,{\frac {2k-1}{2q}}\right)\cos {\frac {(2k-1)\pi p}{q}}$

e

$E_{2n}\left({\frac {p}{q}}\right)=(-1)^{n}{\frac {4(2n)!}{(2\pi q)^{2n+1}}}\sum _{k=1}^{q}\zeta \left(2n+1,{\frac {2k-1}{2q}}\right)\sin {\frac {(2k-1)\pi p}{q}}$

Inoltre,

$\zeta \left(s,{\frac {2p-1}{2q}}\right)=2(2q)^{s-1}\sum _{k=1}^{q}\left[C_{s}\left({\frac {k}{q}}\right)\cos \left({\frac {(2p-1)\pi k}{q}}\right)+S_{s}\left({\frac {k}{q}}\right)\sin \left({\frac {(2p-1)\pi k}{q}}\right)\right]$

vale per ogni $1\leq p\leq q$. $C_{\nu }(x)$ e $S_{\nu }(x)$ sono definite per mezzo della funzione chi di Legendre $\chi _{\nu }$,

$C_{\nu }(x)=\operatorname {Re} \,\chi _{\nu }(e^{ix})$

e

$S_{\nu }(x)=\operatorname {Im} \,\chi _{\nu }(e^{ix}).$

Per valori interi di $\nu$, possono essere espressi in termini dei polinomi di Eulero. Si possono derivare queste relazioni utilizzando l'equazione funzionale insieme alla formula di Hurwitz.

Espansioni in serie

Serie di Taylor

La derivata della funzione zeta di Hurwitz rispetto alla seconda variabile è una traslazione:

${\frac {\partial }{\partial q}}\zeta (s,q)=-s\zeta (s+1,q).$

Perciò, la serie di Taylor ha la caratteristica forma umbrale:

$\zeta (s,x+y)=\sum _{k=0}^{\infty }{\frac {y^{k}}{k!}}{\frac {\partial ^{k}}{\partial x^{k}}}\zeta (s,x)=\sum _{k=0}^{\infty }{s+k-1 \choose s-1}(-y)^{k}\zeta (s+k,x).$

Alternativamente,

$\zeta (s,q)={\frac {1}{q^{s}}}+\sum _{n=0}^{\infty }(-q)^{n}{s+n-1 \choose n}\zeta (s+n),$

con $|q|<1$.

Strettamente connessa è la formula di Stark–Keiper:

$\zeta (s,N)=\sum _{k=0}^{\infty }\left[N+{\frac {s-1}{k+1}}\right]{s+k-1 \choose s-1}(-1)^{k}\zeta (s+k,N)$

che vale per $N$ intero e $s$ arbitrario. Vedere la formula di Faulhaber per una relazione simile sulle somme finite di potenze di interi.

Serie di Laurent

L'espansione in serie di Laurent può essere utilizzata per definire le costanti di Stieltjes che compaiono nella serie

$\zeta (s,q)={\frac {1}{s-1}}+\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{n!}}\gamma _{n}(q)\;(s-1)^{n}.$

In particolare, $\gamma _{0}(q)=-\psi (q)$ e$\gamma _{0}(1)=-\psi (1)=\gamma _{0}=\gamma$.

Legami con altre funzioni

Legame con i polinomi di Bernoulli

La funzione $\beta$ definita precedentemente generalizza i polinomi di Bernoulli:

$B_{n}(x)=-\Re \left[(-i)^{n}\beta (x;n)\right]$

dove $\Re (z)$ indica la parte reale di $z$. Alternativamente,

$\zeta (-n,x)=-{B_{n+1}(x) \over n+1}.$

In particolare, la relazione vale per $n=0$ e si ha

$\zeta (0,x)={\frac {1}{2}}-x.$

Legame con la funzione theta di Jacobi

Se $\vartheta (z,\tau )$ è la funzione theta di Jacobi, allora

$\int _{0}^{\infty }\left[\vartheta (z,it)-1\right]t^{s/2}{\frac {dt}{t}}=\pi ^{-(1-s)/2}\Gamma \left({\frac {1-s}{2}}\right)\left[\zeta (1-s,z)+\zeta (1-s,1-z)\right]$

vale per $\operatorname {Re} (s)>0$ e $z$ complesso, ma non intero. Per $z$ intero , la formula diventa

$\int _{0}^{\infty }\left[\vartheta (n,it)-1\right]t^{s/2}{\frac {dt}{t}}=2\ \pi ^{-(1-s)/2}\ \Gamma \left({\frac {1-s}{2}}\right)\zeta (1-s)=2\ \pi ^{-s/2}\ \Gamma \left({\frac {s}{2}}\right)\zeta (s).$

dove $\zeta$ è la funzione zeta di Riemann. Si noti che questa ultima forma è l'equazione funzionale della funzione zeta di Riemann, come scritta in origine da Riemann. La distinzione tra $z$ intero e non tiene conto del fatto che la funzione theta di Jacobi converge alla funzione delta di Dirac in $z$ se $t\rightarrow 0$.

Legame con le funzioni L di Dirichlet

Se l'argomento è un numero razionale, si può esprimere la funzione zeta di Hurwitz come combinazione lineare di funzioni L di Dirichlet e vice versa: La Zeta di Hurwitz coincide con la Zeta di Riemann $\zeta (s)$ quando $q=1$, se $q=1/2$ è uguale a $(2^{s}-1)\zeta (s)$, e se $q=n/k$ con $k>2$, $(n,k)>1$ e $0<n<k$, allora

$\zeta (s,n/k)={\frac {k^{s}}{\varphi (k)}}\sum _{\chi }{\overline {\chi }}(n)L(s,\chi ),$

dove la somma è sui caratteri di Dirichlet mod $k$. Nella direzione opposta si ha la combinazione lineare

$L(s,\chi )={\frac {1}{k^{s}}}\sum _{n=1}^{k}\chi (n)\;\zeta \left(s,{\frac {n}{k}}\right).$

Esiste anche il teorema di moltiplicazione

$k^{s}\zeta (s)=\sum _{n=1}^{k}\zeta \left(s,{\frac {n}{k}}\right),$

di cui una utile generalizzazione è la relazione di distribuzione

$\sum _{p=0}^{q-1}\zeta (s,a+p/q)=q^{s}\,\zeta (s,qa).$

(Questa ultima forma è valida solo se $q$ è un numero naturale e $1-qa$ non lo è.)

Zeri

Se $q=1$, la funzione zeta di Hurwitz si riduce alla funzione zeta di Riemann; se $q=1/2$ si riduce alla funzione zeta di Riemann moltiplicata per una semplice funzione di variabile complessa $s$ (vide supra), riconducendosi in ogni caso al difficile studio degli zeri della Zeta di Riemann. In particolare, non esistono zeri con parte reale maggiore o uguale a 1. Tuttavia, se $0<q<1$ e $q\neq 1/2$, allora esistono degli zeri della funzione zeta di Hurwitz nella fascia $1<\operatorname {Re} (s)<1+\epsilon$ per ogni $\epsilon$ reale positivo. Questo fatto fu dimostrato da Davenport e Heilbronn per $q$ razionale o trascendente, e da Cassels per gli irrazionali algebrici.

Applicazioni

La funzione zeta di Hurwitz compare in svariate discipline. Più comunemente, si presenta nella teoria dei numeri, dove il suo studio è il più profondo e sviluppata. Tuttavia, compare anche nello studio dei frattali e dei sistemi dinamici. Nella statistica applicata, è presente nella legge di Zipf e in quella di Zipf–Mandelbrot. Nella fisica delle particelle, compare in una formula di Julian Schwinger, fornendo un risultato esatto della velocità di produzione di coppia di un elettrone di Dirac.

Casi speciali e generalizzazioni

La funzione zeta di Hurwitz con $m$ un intero positivo è collegata alla funzione poligamma:

$\psi ^{(m)}(z)=(-1)^{m+1}m!\zeta (m+1,z)\ .$

Per interi negativi $-n$, i valori sono collegati ai polinomi di Bernoulli:

$\zeta (-n,x)=-{\frac {B_{n+1}(x)}{n+1}}\ .$

La funzione zeta di Barnes generalizza la Zeta di Hurwitz come

$\zeta _{N}(s,w|a_{1},...,a_{N})=\sum _{n_{1},\dots ,n_{N}\geq 0}{\frac {1}{(w+n_{1}a_{1}+\cdots +n_{N}a_{N})^{s}}}$

dove $w$ e $a_{j}$ hanno parte reale positiva e $\operatorname {Re} (s)>N$.

Un'ulteriore generalizzazione viene dalla funzione trascendente di Lerch:

$\Phi (z,s,q)=\sum _{k=0}^{\infty }{\frac {z^{k}}{(k+q)^{s}}}$

e quindi

$\zeta (s,q)=\Phi (1,s,q).\,$

Infine compaiono la funzione ipergeometrica

$\zeta (s,a)=a^{-s}\cdot {}_{s+1}F_{s}(1,a_{1},a_{2},\ldots a_{s};a_{1}+1,a_{2}+1,\ldots a_{s}+1;1)$ dove $a_{1}=a_{2}=\ldots =a_{s}=a{\text{, }}a\notin \mathbb {N} {\text{ e }}s\in \mathbb {N} ^{+}.$

e la funzione G di Meijer

$\zeta (s,a)=G\,_{s+1,\,s+1}^{\,1,\,s+1}\left(-1\;\left|\;{\begin{matrix}0,1-a,\ldots ,1-a\\0,-a,\ldots ,-a\end{matrix}}\right)\right.\qquad s\in \mathbb {N} ^{+}.$

Bibliografia

• Apostol, T. M. (2010), "Hurwitz zeta function", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, MR 2723248
• vedere capitolo 12 di Apostol, T. M. (1976), Introduction to analytic number theory, Undergraduate Texts in Mathematics, New York-Heidelberg: Springer-Verlag, ISBN 978-0-387-90163-3, MR 0434929, Zbl 0335.10001
• Milton Abramowitz and Irene A. Stegun, Handbook of Mathematical Functions, (1964) Dover Publications, New York. ISBN 0-486-61272-4. (vedere Paragrafo 6.4.10 per le relazione con la funzione poligamma.)
• Harold Davenport, Multiplicative number theory, Lectures in advanced mathematics, vol. 1, Chicago, Markham, 1967, Zbl 0159.06303.
• Jeff Miller e Victor S. Adamchik, Derivatives of the Hurwitz Zeta Function for Rational Arguments, in Journal of Computational and Applied Mathematics, vol. 100, 1998, pp. 201–206, DOI:10.1016/S0377-0427(98)00193-9. URL consultato il 1º maggio 2019 (archiviato dall'url originale il 17 marzo 2010).
• Linas Vepstas, The Bernoulli Operator, the Gauss–Kuzmin–Wirsing Operator, and the Riemann Zeta (PDF), su linas.org.
• István Mező e Ayhan Dil, Hyperharmonic series involving Hurwitz zeta function, in Journal of Number Theory, vol. 130, n. 2, 2010, pp. 360–369, DOI:10.1016/j.jnt.2009.08.005.

Voci correlate

• Funzione zeta di Riemann
• Funzione speciale
• Funzione Gamma
• Polinomio di Bernoulli
• Trasformata di Mellin
• Teoria analitica dei numeri

Collegamenti esterni

• (EN) Eric W. Weisstein, Funzione zeta di Hurwitz, su MathWorld, Wolfram Research.