Equazione di Bernoulli

Principio o Teorema di Bernoulli.

Acqua in caduta

In fluidodinamica, l'equazione o Teorema di Bernoulli rappresenta una particolare forma semplificata delle equazioni di Navier-Stokes, ottenuta in caso di flusso non viscoso (ovvero flusso nel quale la viscosità può essere trascurata), dall'integrazione lungo una linea di flusso, e descrive il moto di un fluido lungo tale linea.

L'equazione rappresenta matematicamente il principio di Bernoulli (o effetto Bernoulli) che descrive il fenomeno per cui in un fluido ideale su cui non viene applicato un lavoro, per ogni incremento della velocità si ha simultaneamente una diminuzione della pressione o un cambiamento nell'energia potenziale gravitazionale del fluido. Prende il nome dello scienziato svizzero Daniel Bernoulli (1700 - 1782), nonostante fosse già noto in precedenza ad altri studiosi, fra cui Eulero.

Per la validità del teorema di Bernoulli non è necessario che il fluido sia non viscoso puntualmente ma è nulla la risultante di tali azioni viscose che sono legate al rotore della vorticità, ma basta che il flusso sia incomprimibile, irrotazionale (potenziale) e stazionario (derivata euleriana nulla).

In queste ipotesi, le equazioni di Navier-Stokes possono essere ridotte ad una forma semplificata (equazioni di Eulero), che, integrate lungo una linea di flusso, conducono all'equazione di Bernoulli, che può essere espressa nella forma:

$p + \rho{v^2 \over 2} + \rho gh = \mathrm{costante}$

in cui:

• v rappresenta la velocità del fluido lungo la linea di flusso,
• g è l'accelerazione di gravità,
• h è la quota altimetrica (ovvero l'altezza rispetto ad un riferimento orizzontale, di un qualsiasi punto all`interno del condotto),
• p rappresenta la pressione di tipo statico lungo la linea di flusso,
• ρ è la densità del fluido.

Il teorema di Bernoulli senza calcolo integrale

Il teorema di Bernoulli può essere dimostrato anche senza ricorrere al calcolo integrale.

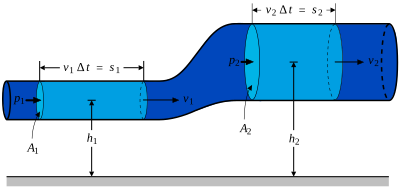
Il lavoro compiuto dalle forze di superficie per spostare il fluido di un tratto $\Delta l$ è pari a

$L_1 = p_1 S_1\Delta l = p_1V_1$

dove $p_1$ è la pressione agente sulla sezione $S_1$, e $V_1$ è il volume di fluido che ha attraversato $\Delta l$.

Analogamente sarà necessario un lavoro per spostare il fluido presente in una sezione a valle di $S_2$. Tale lavoro sarà:

$L_2 = -p_2V_2$

Ne segue che il lavoro totale compiuto dalle forze di superficie è:

$L_S = L_1 + L_2 = p_1V_1 - p_2V_2$

Il lavoro compiuto dalle forze di volume per spostare il fluido dall'altezza $h_1$ all'altezza $h_2$ corrisponderà alla variazione di energia potenziale gravitazionale:

$L_V = mgh_1 - mgh_2$

La somma di $L_S$ ed $L_V$, sarà uguale alla variazione di energia cinetica:

$L_S + L_V = {1 \over 2}mv_2^2 - {1 \over 2}mv_1^2$

da cui segue che:

$p_1V_1 - p_2V_2 + mgh_1 - mgh_2= {1 \over 2}mv_2^2 - {1 \over 2}mv_1^2$

che equivale a:

$p_1V_1 + mgh_1 + {1 \over 2}mv_1^2 = p_2V_2 + mgh_2 + {1 \over 2}mv_2^2$

dividendo quindi ambo i membri per il volume si ottiene:

$p_1 + \rho gh_1 + {1 \over 2}\rho v_1^2 = p_2 + \rho gh_2 + {1 \over 2}\rho v_2^2$

che equivale a dire:

$p + \rho gh + {1 \over 2}\rho v^2 = \mathrm{costante}$

in cui:

• p è la pressione
• ρ è la densità (costante) del fluido
• v è la velocità
• g è l'accelerazione di gravità
• h è l'altezza.

Applicazioni del teorema di Bernoulli

Velocità di efflusso torricelliana

Per approfondire, vedi Legge di Torricelli.

L'applicazione più famosa del teorema di Bernoulli è il calcolo della velocità di fuoriuscita di un fluido da un recipiente forato.

Si consideri un recipiente di forma qualsiasi riempito di un fluido, su cui è stato praticato un foro all'altezza $h_0 = 0$. Considerando come $A_1$ la sezione del recipiente, $h$ l'altezza relativa ad $h_0$ a cui si trova la superficie libera del liquido e $A_2$ la sezione del foro si ottiene:

$p_1 + \rho gh + {1 \over 2}\rho v_1^2 = p_2 + \rho gh_0 + {1 \over 2}\rho v_2^2$

ma $p_1 = p_2$ quindi:

$\rho gh + {1 \over 2}\rho v_1^2 = \rho gh_0 + {1 \over 2}\rho v_2^2$

Dal momento che $h_0 = 0$

$\rho gh + {1 \over 2}\rho v_1^2 = {1 \over 2}\rho v_2^2$

Siccome il flusso è costante, $v_1$ è trascurabile rispetto a $v_2$ (poiché $A_1 \gg A_2$), per cui:

$\rho gh = {1 \over 2}\rho v_2^2$

da cui segue

$v_2^2 = 2gh$

o

$v_2 = \sqrt{2gh}$

anche detta velocità di efflusso torricelliana poiché Torricelli giunse allo stesso risultato nel 1644 prima dei lavori di Bernoulli.

Portanza

Per approfondire, vedi Portanza.

Effetto di Bernoulli su un profilo alare

L'equazione di Bernoulli è anche in grado di quantificare (entro certi limiti) la portanza, ovvero la componente della forza normale al moto del fluido che agisce su un corpo immerso.

La portanza è data infatti dalla differenza di velocità che si ottiene volutamente dalla particolare forma dell'ala, che è costruita in modo da rendere la velocità dell'aria sulla faccia superiore maggiore di quella sulla faccia inferiore. Questa tecnica permette di generare una forza diretta verso l'alto data da una pressione sulla faccia inferiore maggiore di quella sulla faccia superiore.

$p_i + {1 \over 2}\rho v_i^2 = p_s + {1 \over 2}\rho v_s^2$

• $p_i$: pressione dell'aria sulla faccia inferiore
• $v_i$: velocità dell'aria sulla faccia inferiore
• $p_s$: pressione dell'aria sulla faccia superiore
• $v_s$: velocità dell'aria sulla faccia superiore

Quindi la differenza di pressione tra la faccia inferiore e superiore dell'ala sarà:

$(p_i-p_s) = {1 \over 2}\rho v_s^2 - {1 \over 2}\rho v_i^2$

Questa differenza di pressione ($p_i-p_s$) ha semplicemente l'effetto di una pressione $p$ della stessa intensità di ($p_i-p_s$): infatti viene prodotta una forza che è direttamente proporzionale alla superficie inferiore dell'ala. Infatti, per definizione:

$p = {F \over A}$

quindi la forza risultante sarà:

$F = pA$

Il principio di Bernoulli non basta tuttavia per spiegare il fenomeno della portanza; si deve considerare anche l'effetto della curvatura delle linee di corrente sul profilo e la deviazione di esse verso il basso (Effetto Coandă).

Altri effetti spiegabili con l'equazione di Bernoulli

Ci sono molti fenomeni della vita di tutti i giorni che sono spiegabili tramite l'equazione di Bernoulli:

• il distacco e la distruzione dei tetti delle costruzioni che vengono colpite da venti molto forti (durante uragani o eventi atmosferici molto violenti): infatti in questi casi le costruzioni, che sono al loro interno approssimativamente isolate rispetto all'esterno, sono sottoposte ad una grande differenza di pressione causata dalla forte velocità dell'aria esterna, che produce una diminuzione della pressione esterna, mentre la pressione all'interno della casa rimane invariata. La forza esercitata sulla superficie del tetto dalla differenza di pressione (che va dal basso verso l'alto) è capace di scoperchiarlo;

• l'aterosclerosi è una malattia provocata dall'accumulo di materiale lipidico(grasso) nello strato più interno delle arterie. Per l'equazione di Bernoulli ad una diminuzione della sezione della cavità dove scorre il liquido (in questo caso sangue) corrisponde un aumento di velocità di quest'ultimo il quale provoca un abbassamento della pressione interna in quel punto. Di conseguenza la pressione esterna sarà maggiore di quella interna e tenderà a schiacciare l'arteria così da diminuire ulteriormente il flusso di sangue;

• la chiusura di una porta in una stanza attraversata dal vento, anche nel caso in cui il vento soffi nella direzione in cui la porta dovrebbe aprirsi: questo perché la velocità dell'aria causa una depressione che induce il movimento della porta stessa.

Nei casi citati è possibile trascurare il termine gravitazionale dell'equazione di Bernoulli, in quanto le linee di flusso a cui si fa riferimento hanno approssimativamente la stessa energia potenziale.

Voci correlate

• Fluidodinamica
• Aerodinamica
• Effetto Venturi
• Flusso potenziale
• Flusso laminare
• Daniel Bernoulli
• Legge di Torricelli
• Principio di Archimede
• Equazione di Bernoulli instazionaria
• Teorema di Kutta-Žukovskij

Altri progetti

• Commons

• Commons contiene immagini o altri file su Equazione di Bernoulli

Portale Meccanica: accedi alle voci di Wikipedia che trattano di meccanica