Vettore di Lenz

In meccanica classica, il Vettore di Laplace-Rouge-Lenz (o semplicemente Vettore di Lenz) è un vettore utilizzato comunemente per descrivere la forma e l'orientazione dell'orbita di un corpo celeste attorno ad un altro, come nel caso della rivoluzione di un pianeta attorno al sole. Per due corpi interagenti secondo la gravità Newtoniana, il vettore di Lenz è una costante del moto, nel senso che esso, per una data orbita, conserva il suo aspetto indipendentemente dal punto o dal momento in cui esso venga calcolato ; in modo equivalente, si può dire che il vettore venga “conservato” durante il moto. Più in generale, questo vettore risulta conservato in tutti i problemi in cui due corpi interagiscono mediante una forza centrale che varia secondo la legge dell'inverso del quadrato delle distanza; tali problemi sono soprannominati Problemi di Keplero .

L'atomo di idrogeno è un esempio di problema di questo tipo, in quanto comprende due particelle cariche interagenti attraverso la Forza di Coulomb. Il vettore di Lenz rivestì una importantissima funzione nella prima derivazione quantistica dello spettro di emissione dell'atomo di idrogeno prima dello sviluppo dell'Equazione di Schrödinger. Tuttavia, questo approccio oggi è scarsamente utilizzato.

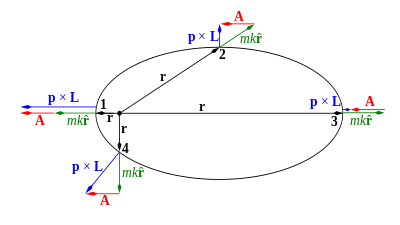
In meccanica classica e quantistica, quantità conservate generalmente corrispondono a simmetrie del sistema. La conservazione del vettore di Lenz corrisponde ad una simmetria alquanto inusuale:il problema di Keplero è infatti matematicamente equivalente a quello di una particella in moto libero sul confine tridimensionale di una ipersfera,, cosicchè l'intero problema risulta simmetrico rispetto certe rotazioni di questo spazio quadri-dimensionale. Questa alta simmetria è il risultato di due proprietà del problema di Keplero: il vettore velocità si muove su di un cerchio perfetto e, per una energia meccanica predisposta, tutti questi cerchi di velocità si intersecano insieme negli stessi due punti.

Molte generalizzazioni del vettore di Lenz sono state elaborate con lo scopo di incorporare gli effetti della relatività speciale, campi elettromagnetici o altri tipi di forze centrali.

Contesto

Una singola particella in moto dentro un campo di forze conservative possiede al massimo quattro costanti del moto: l'energia totale E e le tre componenti cartesiane del momento angolare L. L'orbita della particella è confinata in un piano definito dal momento iniziale p (o, equivalentemente, la velocità v) ed il raggio vettore r fra la particella stessa ed il centro del campo di forze.

Così come è stato definito precedentemente, il vettore di Lenz A giace sempre sul piano orbitale di qualsiasi forza centrale. Tuttavia, esso risulta costante solo per una forza centrale che decresca secondo la legge dell'inverso del quadrato. Per la maggior parte delle forze centrali, invece, A non è costante, ma cambia sia in lunghezza che in direzione; se la forza risponde solo approssimativamente al criterio sopra citato, il vettore A è piuttosto costante in lunghezza, ma ruota lentamente direzione. È altresì possibile una forma più generale del vettore di Lenz, indicata con ${\mathcal {A}}$, ma questo nuovo vettore risulta essere una funzione piuttosto complicata della posizione, ed in genere non può essere espresso in forma compatta.

Il piano su cui si svolge il moto è perpendicolare al vettore momento angolare L, che è costante; questa proprietà geometrica può essere espressa matematicamente con l'equazione del prodotto scalare fra vettori r·L=0; analogamente, poiché A giace nel medesimo piano, A·L = 0.

Storia della riscoperta

Il vettore di Lenz A è una costante del moto all'interno del problema di Keplero, ed è utile per descrivere le orbite dei corpi celesti, come il caso del moto di un pianeta attorno al Sole. Ciò nondimeno, esso è stato per lungo tempo poco conosciuto ed utilizzato fra i fisici, possibilmente poichè esso risulta meno intuitivo di altre quantità come il momento ed il momento angolare. Di conseguenza, esso è stato "riscoperto" indipendentemente diverse volte negli ultimi tre secoli. Jakob Hermannè stato il primo a dimostrare che A è una costante nel caso delle forze centrali con proporzionalità quadratica inversa, e portò avanti gli studi riguardo la sua connessione all'eccentricità delle orbite celesti. Il suo lavoro venne generalizzato nella sua forma moderna da Johann Bernoulli nel 1710. Alla fine del secolo, Pierre-Simon de Laplace riscoprì la conservazione di A, derivandola analiticamente, invece che geometricamente. Nella metà del diciannovesimo secolo, William Rowan Hamilton elaborò l'equivalente vettore eccentricità e lo utilizzò per dimostrare che il vettore momento p si muove lungo un cerchio per moti in campi di forze centrali (Figura 3). all'inizio del ventesimo secolo, [Josiah Willard Gibbs]] derivò lo stesso vettore utilizzando metodi di analisi vettoriale. La derivazione di Gibbs fu utilizzata a mo' di esempio da Carle Runge in un popolare libro di testo tedesco sui vettori, che fu a sua volta citato da Wilhelm Lenz nel suo testo sulla (vecchia) trattazione in meccanica quantistica dello spettro dell'atomo di idrogeno. Nel 1926, il vettore fu utilizzato da Wolfgang Pauli per ottenere lo spettro dell'idrogeno utilizzando la formulazione matriciale della meccanica quantistica, ma non l'equazione di Schrödinger; dopo la pubblicazione di Pauli, esso divenne noto come "vettore di Rouge-Lenz".

Definizione matematica

Per una singola particella in moto dentro un campo di forze centrali decritto dall'equazione $\mathbf {F} (r)={\frac {-k}{r^{2}}}\mathbf {\hat {r}}$, il vettore di Lenz A è definito dalla formula

Figura 1: Il vettore di Lenz A (in rosso) in quattro punti (indicati 1, 2, 3 e 4) sull'orbita ellittica di un punto materiale in moto in un campo di forze centrali. Il centro di attrazione è indicato con un piccolo cerchio nero da cui si origina il vettore posizione (nero). Il vettore momento angolare L è perpendicolare all'orbita. I vettori complanari p×L e (mk/r)r sono in blu ed in verde, rispettivamente. Il vettore A è costante in direzione e modulo.

$\mathbf {A} =\mathbf {p} \times \mathbf {L} -mk\mathbf {\hat {r}}$

dove

• $m\!\,$ è la massa del punto materiale,
• $\mathbf {p} \!\,$ è il vettore quantità di moto,
• $\mathbf {L} =\mathbf {r} \times \mathbf {p} \!\,$ è il vettore momento angolare,
• $k\!\,$ è il parametro che descrive l'intensità della forza centrale,
• $\mathbf {r} \!\,$ è il vettore posizione della particella (Figura 1), e
• $\mathbf {\hat {r}} \!\,$ è il corrispondente vettore unitario, $\mathbf {\hat {r}} ={\frac {\mathbf {r} }{r}}$ dove r è il modulo di r.

Poiché la forza considerata è conservativa, l'energia totale E è una costante del moto

$E={\frac {p^{2}}{2m}}-{\frac {k}{r}}={\frac {1}{2}}mv^{2}-{\frac {k}{r}}$

In oltre, essa è anche una forza centrale, e perciò il vettore momento angolare L è anch'esso conservato e definisce il piano in cui la particella si muove. Il vettore di Lenz A è perpendicolare al momento angolare L poiché sia p × L che r sono perpendicolari a L. Da ciò segue che A giace nel piano dell'orbita.

Questa definizione del vettore di Lenz inerisce ad un singolo punto materiale di massa m in moto sotto l'azione di una forza fissa. Tuttavia, la stessa definizione può essere estesa al caso di due corpi come il problema di Keplero, ponendo m pari alla massa ridotta dei due corpi ed r come il raggio vettore fra i due corpi.

Molte varianti al vettore di Lenz possono essere utilizzate per esprimere la stessa costante del moto. La più utilizzata è il vettore eccentricità, ottenuta da A dopo una divisione per $mk$.

$\mathbf {e} ={\frac {\mathbf {A} }{mk}}={\frac {1}{mk}}(\mathbf {p} \times \mathbf {L} )-\mathbf {\hat {r}}$

Derivazione della geometria orbitale

Figura 2: Versione semplificata della Figura 1, con rappresentato l'angolo θ fra A ed r in un punto dell'orbita.

Forma ed orientamento dell'orbita può essere determinata a partire dal vettore di Lenz come segue. Eseguendo il prodotto scalare fra A ed il vettore posizione r si ottiene l'equazione

$\mathbf {A} \cdot \mathbf {r} =Ar\cos \theta =\mathbf {r} \cdot \left(\mathbf {p} \times \mathbf {L} \right)-mkr$

dove θ è l'angolo fra r ed A (Figura 2). Permutando il triplo prodotto scalare

$\mathbf {r} \cdot \left(\mathbf {p} \times \mathbf {L} \right)=\left(\mathbf {r} \times \mathbf {p} \right)\cdot \mathbf {L} =\mathbf {L} \cdot \mathbf {L} =L^{2}$

e riordinando si ottiene la formula, valida per le sezioni coniche

${\frac {1}{r}}={\frac {mk}{L^{2}}}\left(1+{\frac {A}{mk}}\cos \theta \right)$

dell'eccentricità $e\!\,$

$e={\frac {A}{mk}}={\frac {\left|\mathbf {A} \right|}{mk}}$

ed il lato retto

$\left|4p\right|={\frac {2L^{2}}{mk}}$

Il semiasse maggiore a della sezione conica può essere definito a partire dal lato retto e dall'eccentricità

$a\left(1\pm e^{2}\right)=2p={\frac {L^{2}}{mk}}$

dove il segno meno è proprio dell' ellisse ed il segno più dell' iperbole.

Il prodotto scalare di A con se stesso dà origine ad una equazione contenente l'energia meccanica E

$A^{2}=m^{2}k^{2}+2mEL^{2}\,$

che può essere scritta in termini di eccentricità

$e^{2}-1={\frac {2L^{2}}{mk^{2}}}E$

Dunque, se l'energia E è negativa (orbita chiusa), l'eccentricità è più piccola di uno e l'orbita è una ellisse. Al contrario, se l'energia è positiva (orbita aperta), l'eccentricità è più grande di uno e l'orbita è rappresentata da una iperbole. In fine, se l'energia è esattamente zero, l'eccentricità è uno e l'orbita ha forma parabolica. In tutti i casi considerati, la direzione di A giace lungo l'asse di simmetria della sezione conica e punta dal centro della forza verso l'apside, il punto di massima vicinanza.

Odografo circolare del momento

Figura 3: Il vettore momento p (in blu) si muove su di un cerchio mentre la particella si muove lungo una ellisse. I quattro punti evidenziati corrispondono a quelli in Figura 1. il cerchio è centrato sull'asse y in posizione A/L (in magenta), con raggio mk/L (verde). L'angolo η determina l'eccentricità e dell'orbita ellittica (cos η = e).

la conservazione del vettore di Lenz A e del vettore momento angolare L è molto utile per mostrare che il vettore momento (quantità di moto) p si muove su di un cerchio nel caso di una forza centrale.

Eseguendo il prodotto scalare di

$mk~{\hat {\mathbf {r} }}=\mathbf {p} \times \mathbf {L} -\mathbf {A}$

con se stesso si ottiene

$(mk)^{2}=A^{2}+p^{2}L^{2}+2\mathbf {L} \cdot (\mathbf {p} \times \mathbf {A} )~.$

In seguito scegliendo L lungo l'asse z, ed il semiasse maggiore come asse x, si ottiene l'equazione per p,

$p_{x}^{2}+\left(p_{y}-A/L\right)^{2}=\left(mk/L\right)^{2}~.$

In altre parole, il vettore quantità di moto p è confinato in un cerchio di raggio mk/L centrato nel punto (0, A/L). L'eccentricità e corrisponde al coseno dell'angolo η mostrato in Figura 3. Nel limite dell'orbita circolare, e dunque all'annullarsi di A, il cerchio possiede centro nell'origine (0,0). Per brevità, è anche utile introdurre la variabile $p_{0}={\sqrt {2m\left|E\right|}}$. Questo odografo circolare è utile per illustrare la simmetria del problema di Keplero.

Costanti del moto e superintegrabilità

Le sette quantità scalari E, A ed L (essendo vettori, gli ultimi due contribuiscono per tre quantità ciascuno) sono correlate da due equazioni, A · L = 0 e A² = m²k² + 2 m E L², dando origine a cinque costanti del moto indipendenti. Questo risultato è coerente con le sei condizioni iniziali (ovvero, i vettori velocità e posizione della particella, di tre componenti ciascuno) che specificano l'orbita del corpo, dato che l'istante di partenza non è determinato da queste costanti. Poiché il modulo di A (e la correlata eccentricità orbitale e) possono essere determinati a partire dal momento angolare L e l'energia E, solo la direzione di A è conservata indipendentemente; in più, poiché A deve essere sempre perpendicolare a L, contribuisce solo con una ulteriore quantità conservata.

Un sistema meccanico con d gradi di libertà può avere al massimo 2d− 1 costanti del moto, poiché ci sono 2d condizioni iniziali e l'istante iniziale non può essere determinato a partire da una costante. Un sistema con più di d costanti del moto è chiamato superintegrabile ed un sistema con 2d− 1 costanti è detto massimamente superintegrabile. Poiché la soluzione dell'Equazione di Hamilton-Jacobi in una coordinata del sistema può fornire solo d costanti del moto, un sistema superintegrabile può essere scomposto in più di un sistema di coordinate. Il problema di Keplero è massimamente superintegrabile, poiché possiede tre gradi di libertà (d=3) e cinque costanti del moto indipendenti; la sua equazione di Hamilton-Jacobi è scomponibile sia in coordinate sferiche che in coordinate paraboliche.

Sistemi massimamente superintegrabili seguono un'orbita chiusa ed unidimensionale all'interno dello spazio delle fasi, poiché l'orbita è data dall'intersezione della isosuperficie delle costanti del moto. Conseguentemente, le orbite sono perpendicolari a tutti i gradienti di tutte queste isosuperfici indipendenti, cinque in questo specifico caso, e quindi sono determinate dal prodotto vettoriale generalizzato di tutti questi gradienti. Come risultato, tutti i sistemi superintegrabili sono automaticamente descritti dalla meccanica di Nambu, o, equivalentemente, dalla Meccanica Hamiltoniana. I sistemi massimamente superintegrabili possono essere quantizzati usando relazioni commutative. Ciò nondimeno, in modo equivalente, possono anche essere quantizzati nell'insieme di relazioni di Nambu, come per il classico problema d i Keplero nell'atomo di idrogeno.