Parità dello zero

La parità dello zero è una nozione matematica caratterizzata, nonostante la sua semplicità, da limitata consapevolezza nella popolazione delle società occidentali, dovuta a bias cognitivo e spesso a fraintendimenti del concetto nel percorso di istruzione scolastica inferiore. Lo zero è infatti un numero pari in quanto ne soddisfa banalmente la definizione, essendo un multiplo intero di 2 dato dal fatto che 0 × 2 = 0. Ciononostante, una percentuale significativa di studenti, adulti e insegnanti nutre convinzioni errate sull'argomento, e tra le più comuni vi è l'idea che zero non sia né pari né dispari.
Le regole di parità dell'aritmetica (come pari - pari = pari) richiedono che lo 0 sia pari. Lo 0 è l'elemento neutro additivo dell'insieme degli interi pari ed è l'elemento a partire dal quale tutti gli altri numeri naturali pari sono definiti ricorsivamente. Alcune applicazioni di questa ricorsione, utilizzate dalla teoria dei grafi alla geometria computazionale, si basano sul fatto che lo 0 sia pari. Oltre ad essere divisibile per 2, lo 0 è divisibile per ogni intero positivo. Nel sistema numerico binario utilizzato dai computer, è particolarmente importante che lo 0 sia divisibile per ogni potenza di 2: in questo senso, 0 è il numero "più pari" di tutti.
Tra il pubblico in generale, la parità di 0 può essere fonte di confusione, solitamente a causa di una non ottimale educazione matematica. In esperimenti sul tempo di reazione, la maggior parte delle persone è più lenta a identificare 0 come pari di quanto sia veloce ad identificare come pari 2, 4, 6, o 8. Alcuni studenti di matematica (e talvolta anche alcuni insegnanti), pensano che lo 0 sia dispari, o sia pari che dispari, o nessuno dei due. I ricercatori in didattica della matematica propongono di usare queste idee sbagliate come opportunità di apprendimento. Lo studiare uguaglianze come 0 × 2 = 0 può rendere visibili i dubbi degli studenti nel chiamare lo 0 un numero e nell'utilizzarlo in aritmetica. Il discuterne in classe può portare gli studenti ad apprezzare i principi fondamentali del ragionamento matematico, come ad esempio l'importanza delle definizioni. Valutare la parità di questo numero particolare è uno dei primi esempi di un tema importantissimo in matematica: l'astrazione di un concetto familiare a un ambiente non familiare.
Perché zero è pari[modifica | modifica wikitesto]
La definizione tradizionale di "numero pari" può essere usata per dimostrare direttamente che 0 è pari. Un numero viene chiamato "pari" se è un multiplo intero di 2. Come esempio, la ragione per cui 10 è pari è che è uguale a 5 × 2. Allo stesso modo, 0 è un multiplo intero di 2, in particolare 0 × 2 = 0, quindi 0 è pari.[1]
È anche possibile spiegare perché 0 è pari senza riferimento a definizioni formali.[2] Le seguenti spiegazioni illustrano l'idea che 0 è pari in termini di concetti numerici fondamentali. Da questa base, si può fornire fondamento logico per la definizione stessa e la sua applicabilità a 0.
Spiegazioni di base[modifica | modifica wikitesto]

Zero è un numero, e i numeri sono usati per contare. Dato un insieme di oggetti, si usa un numero per indicare quanti oggetti ci sono. Zero è il conteggio nessun oggetto, in termini più formali, è il numero di oggetti presenti in un insieme vuoto. Il concetto di parità viene utilizzato per fare dei gruppi di due oggetti. Se gli oggetti in un insieme possono essere divisi in gruppi da due, senza che rimanga nessun oggetto, allora il numero di oggetti iniziale è pari. Se un oggetto rimane, allora il numero di oggetti è dispari. L'insieme vuoto contiene zero gruppi da due, e nessun oggetto è lasciato fuori da questo raggruppamento, quindi zero è pari.[4]
Queste idee possono essere illustrate disegnando oggetti a coppie. È difficile descrivere zero gruppi da due, o sottolineare la non esistenza di un oggetto rimasto, quindi è utile disegnare altri gruppi e confrontarli con zero. Ad esempio, in un gruppo di cinque oggetti, vi sono due coppie. Ancora più importante, c'è un oggetto residuo, quindi 5 è dispari. Nel gruppo di quattro oggetti, non c'è oggetto avanzato, quindi 4 è pari. Nel gruppo di un solo oggetto, non ci sono coppie, e c'è un oggetto avanzato, di conseguenza 1 è dispari. Nel gruppo di 0 oggetti, non c'è nessun oggetto avanzato, quindi 0 è pari.[5]
C'è un'altra definizione concreta di numero pari: se gli oggetti in un insieme possono essere divisi in due gruppi di uguale dimensione, allora il numero di oggetti è pari. Questa definizione è equivalente alla prima. Anche in questo caso, lo 0 è pari perché l'insieme vuoto può essere diviso in due gruppi di elementi entrambi contenenti 0 elementi e di conseguenza uguali fra loro (0/2 = 0/2 = 0).
I numeri possono anche essere visualizzati come punti sulla retta dei numeri. Quando i numeri pari e dispari sono rappresentati in modi diversi, lo schema che seguono diventa evidente, soprattutto se sono inclusi anche i numeri negativi:

I numeri pari si alternano ai numeri dispari. A partire da qualsiasi numero pari, contando su o giù di due in due si raggiunge un altro numero pari, e non c'è nessun motivo per saltare lo zero.[6]
Con l'introduzione della moltiplicazione, la parità può essere affrontata in maniera più formale utilizzando espressioni aritmetiche. Ogni numero intero è il risultato di una delle seguenti formule:
- (2 × n ) + 0
- (2 × n ) + 1
I numeri espressi dalla prima formula sono pari, quelli espressi dalla seconda sono dispari. Ad esempio 1 è dispari perché:
- 1 = (2 × 0 ) + 1
e 0 è pari perché:
- 0 = (2 × 0 ) + 0
Fare una tabella di questi risultati rafforza l'immagine della retta dei numeri sopra riportata.[7]
Definizione di numero pari[modifica | modifica wikitesto]
La definizione precisa di un termine matematico, come ad esempio "pari" che significa "multiplo intero di due", è in definitiva una convenzione. Al contrario di "pari", alcuni termini matematici sono costruiti escludendo di proposito i casi banali o degeneri. I numeri primi sono un noto esempio. Prima del XX secolo la definizione di primalità era differente e matematici di rilievo quali Goldbach, Lambert, Legendre, Cayley e Kronecker scrivevano che 1 è un numero primo. La moderna definizione di numero primo è un intero positivo con esattamente 2 divisori, quindi 1 non è primo. Questa definizione è oggi preferita perché essa si adatta in modo più naturale ai teoremi matematici che riguardano i numeri primi. Per esempio il teorema fondamentale dell'aritmetica è più facile da enunciare se 1 non è considerato primo.[8]
Sarebbe possibile ridefinire il termine "pari" in modo che non includa più 0. Tuttavia, in questo caso, la nuova definizione renderebbe più difficile formulare teoremi riguardanti i numeri pari. L'effetto può essere facilmente visto nelle regole algebriche dei numeri pari e dispari.[9] Le regole più importanti riguardano addizione, sottrazione, moltiplicazione:
- pari ± pari = pari;
- dispari ± dispari = pari;
- pari × intero = pari.
Con l'inserimento di valori appropriati nei membri di sinistra di queste uguaglianze, si possono produrre degli 0 nei membri di destra:
- 2 - 2 = 0;
- -3 + 3 = 0;
- 4 × 0 = 0.
Le regole qui sopra sarebbero pertanto errate se 0 non fosse pari.[9] Nella migliore delle ipotesi, queste regole dovrebbero essere modificate. Per esempio, un testo di studio di prova afferma che i numeri pari sono "multipli interi di due", ma afferma anche che zero non è "né pari né dispari".[10] Di conseguenza, le regole del testo per i numeri pari e dispari contengono eccezioni:
- pari ± pari = pari (o zero);
- dispari ± dispari = pari (o zero);
- pari × intero (diverso da zero) = pari.[10]
Fare un'eccezione per zero nella definizione dei numeri pari forza a fare eccezioni in tutte le regole che riguardano i numeri pari. Da un'altra prospettiva, prendendo le regole rispettate dai numeri pari positivi e richiedendo che continuino a funzionare per tutti gli interi si arriva alla conclusione che zero deve essere pari.[9]
Contesti matematici[modifica | modifica wikitesto]
Innumerevoli risultati nella teoria dei numeri invocano il teorema fondamentale dell'aritmetica e le proprietà algebriche dei numeri pari, quindi la scelta della definizione di numero pari ha conseguenze di vasta portata. Ad esempio, il fatto che i numeri positivi abbiano una fattorizzazione unica significa che si può determinare se un numero ha un numero pari o dispari di fattori primi distinti. Poiché 1 non è primo, né ha fattori primi, è un prodotto di 0 primi distinti, poiché 0 è un numero pari, 1 ha un numero pari di fattori primi distinti. Ciò implica che la funzione di Möbius assuma il valore μ(1) = 1, che è necessario affinché essa sia una funzione moltiplicativa e affinché la formula di inversione di Möbius funzioni.[11]
Zero non è dispari[modifica | modifica wikitesto]
Un numero n è dispari se esiste un numero intero k tale che n = 2k + 1. Un modo per dimostrare che 0 è pari è per assurdo: supponiamo che 0 sia dispari. In questo caso per la proprietà appena citata esiste un intero k tale che 0 = 2k + 1. Ma l'unica soluzione reale di quest'equazione è k = -1/2 che non è intero. Contraddizione. Quindi 0 non è dispari.
Quindi, se si dimostra che un numero è dispari, esso sarà necessariamente diverso da 0. Questa osservazione, apparentemente banale, fornisce un ottimo modo per dimostrare che un numero è diverso da 0.
Teoria dei grafi[modifica | modifica wikitesto]
Un risultato classico della teoria dei grafi afferma che un grafo di ordine dispari ha sempre almeno un vertice pari (l'ordine di un grafo è il numero dei suoi vertici). (Già questa affermazione richiede che zero sia pari: il grafo vuoto ha ordine pari e un vertice isolato è pari.)[12] Per dimostrare l'affermazione si dimostra un'affermazione più forte che è più facilmente dimostrabile: ogni grafo di ordine dispari ha un numero dispari di vertici pari. Quest'ultima affermazione è spiegata da un'affermazione ancora più generale, nota come lemma delle strette di mano: qualsiasi grafo ha un numero pari di vertici di grado dispari.[13] Infine, il numero pari di vertici dispari è naturalmente spiegato dalla formula della somma dei gradi.
Il lemma di Sperner è un'applicazione più avanzata della stessa strategia. Il lemma afferma che un certo tipo di colorazione su una triangolazione di un simplesso ha un sottosimplesso che contiene tutti i colori della colorazione. Piuttosto che costruire direttamente una tale simplesso, è più conveniente dimostrare che esiste un numero dispari di tali sottosimplessi attraverso un processo di induzione. Una formulazione più forte del lemma spiega perché questo numero è dispari: esso naturalmente decresce come (n + 1) + n se si considerano le due possibili orientazioni di un simplesso.

Un altro uso della proprietà di 0 di essere pari nella teoria dei grafi è il seguente. Un grafo bipartito è un grafo i cui vertici sono divisi in due colori tali che vertici adiacenti hanno colori differenti. Se un grafo connesso non ha cicli dispari, allora è possibile costruire una bipartizione scegliendo un vertice base v e colorando ogni vertice nero o bianco a seconda se la sua distanza da v è pari o dispari. Poiché la distanza di v da se stesso è 0, e 0 è pari, il vertice base è colorato in modo diverso dai vertici ad esso adiacenti, cioè quelli che sono a distanza 1.[14]
Alternanza fra pari e dispari[modifica | modifica wikitesto]
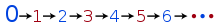
Il fatto che lo 0 sia pari, insieme al fatto che i numeri pari e dispari sono alternati, è sufficiente per determinare la parità di ogni altro numero naturale. Questa idea può essere formalizzata in una definizione ricorsiva dell'insieme dei numeri naturali pari:
- 0 è pari;
- (n + 1) è pari se e solo se n non è pari.
Questa definizione ha il vantaggio concettuale di basarsi solo sugli assiomi minimali dei numeri naturali: l'esistenza di 0 e l'esistenza del successore di un numero. Dunque, è utile per l'implementazione di sistemi logici al computer come LF e l'Isabelle theorem prover.[15] Con questa definizione, la parità di 0 non è un teorema, ma un assioma. Infatti, "0 è un numero pari" può essere interpretato come uno degli assiomi di Peano, di cui tutti gli altri numeri naturali pari sono un modello.[16] Una costruzione simile estende la definizione di parità ai numeri ordinali transfiniti: ogni ordinale limite è pari, compreso lo 0, e i successori degli ordinali limite sono dispari.[17]
Geometria computazionale[modifica | modifica wikitesto]

Il classico test del punto nel poligono della geometria computazionale utilizza le precedenti idee. Per determinare se un punto giace all'interno di un poligono, si considera una semiretta dal punto all'infinito e si conta il numero di volte che la semiretta interseca il bordo del poligono. Il numero di intersezioni è pari se e solo se il punto è esterno al poligono. Questo algoritmo funziona perché, se la semiretta non incrocia mai il poligono, allora il numero di intersezioni è 0, che è pari, e il punto è esterno. Ogni volta che la semiretta incrocia il poligono il numero di intersezioni si alterna tra pari e dispari e il punto tra interno ed esterno.[18]
Algebra astratta[modifica | modifica wikitesto]

In algebra astratta, gli interi pari formano varie strutture algebriche che richiedono l'inclusione dello 0. Il fatto che l'identità additiva (lo 0) sia pari, insieme con la parità delle somme, degli inversi additivi dei numeri pari e dell'associatività dell'addizione, comporta che gli interi pari formano un gruppo. Inoltre, il gruppo degli interi pari rispetto all'addizione è un sottogruppo del gruppo di tutti gli interi (questo è un esempio elementare del concetto di sottogruppo). La precedente osservazione che la regola "pari - pari = pari" forzi 0 a essere pari è un comportamento generale: ogni sottoinsieme non vuoto di un gruppo additivo che è chiuso rispetto alla sottrazione deve essere un sottogruppo e in particolare, deve contenere l'identità.[19]
Poiché gli interi pari formano un sottogruppo degli interi, essi partizionano gli interi in classi laterali. Queste classi laterali possono essere descritte come classi di equivalenza della seguente relazione di equivalenza: x ~ y se (x − y) è pari. Qui la proprietà di 0 di essere pari è direttamente manifestata come la riflessività della relazione binaria ~.[20] Ci sono solo due classi laterali di questo sottogruppo (i numeri pari e i numeri dispari), così esso ha indice 2.
Analogamente, il gruppo alternante è un sottogruppo di indice 2 del gruppo simmetrico su n oggetti. Gli elementi del gruppo alternante, dette permutazioni pari, sono i prodotti di un numero pari di trasposizioni. La funzione identità, che è un prodotto vuoto di trasposizioni, è una permutazione pari poiché 0 è pari ed è l'elemento neutro del gruppo.[21]
La regola "pari × intero = pari" significa che i numeri pari formano un ideale nell'anello degli interi e la precedente relazione d'equivalenza può essere descritta come un'equivalenza modulo questo ideale. In particolare, gli interi pari, sono esattamente quegli interi k con k ≡ 0 (mod 2). Questa formulazione è utile per la ricerca delle radici intere di un polinomio.[22]
Ordine 2-adico[modifica | modifica wikitesto]
Si può stabilire che alcuni multipli di 2 sono "più pari" di altri nel seguente senso. Un numero intero è più pari di un altro se è diviso da una potenza di 2 maggiore. Ad esempio, i multipli di 4 sono doppiamente pari, poiché possono essere divisi per 2 due volte e sono "più pari" di quelli che possono essere divisi per 2 una sola volta. Si ha che 0 non è solo divisibile per 4, ma è l'unico numero ad essere divisibile per ogni potenza di 2, sorpassando quindi tutti gli altri numeri in "essere pari".[23]
Una conseguenza di questo fatto compare nell'ordinamento a bit invertiti dei dati di tipo intero usato da alcuni algoritmi informatici, come la trasformata di Fourier veloce di Cooley-Tukey. Questo ordinamento ha la proprietà che quanto più il primo 1 che compare è a sinistra nell'espansione binaria di un numero, cioè quante più volte esso è divisibile per 2, tanto prima quel numero comparirà. Poiché l'inversione dei bit di 0 è sempre 0, esso può essere diviso per 2 un qualunque numero di volte e la sua espansione binaria non contiene nessun 1, così esso è sempre il primo.[24]
Sebbene 0 sia divisibile per 2 più volte di ogni altro numero, non è immediato quantificare esattamente quante volte lo sia. Per ogni intero non nullo n, si definisce ordine 2-adico, o 2-ordine, di n come il numero di volte che n è divisibile per 2. Questa descrizione non funziona per 0, non importa quante volte 0 è diviso per 2, esso sarà comunque divisibile per 2 ancora una volta. La convenzione utilizzata è porre il 2-ordine di 0 uguale a infinito in questo caso particolare.[25] Questa convenzione non è ristretta al caso 2-adico, ma è un assioma della valutazione additiva in algebra astratta.[26]
Le potenze di 2, cioè 1, 2, 4, 8,..., formano una semplice successione di numeri con 2-ordine crescente. Nell'insieme dei numeri 2-adici tale successione converge, in effetti, a 0.[27]
Educazione[modifica | modifica wikitesto]

Il concetto della parità di zero è trattato spesso nei primi due o tre anni dell'educazione primaria, mentre è introdotto il concetto di numeri pari o dispari.[29]
Conoscenza degli studenti[modifica | modifica wikitesto]
Il grafico a destra[28] descrive le credenze dei bambini circa la parità di zero, man mano che avanzano dal primo al sesto anno del sistema educativo inglese (dai 5 ai 10 anni). I dati provengono da Len Frobisher, che ha condotto due indagini sugli scolari inglesi. Frobisher era interessato a come la conoscenza della parità delle cifre da sole si traducesse nella conoscenza della parità di un numero composto da multiple cifre e zero era importante nei risultati (se un numero termina con 0,2,4,6,8 allora è pari).[30]
In un sondaggio preliminare condotto su circa 400 bambini di sette anni, il 45% ha risposto che zero è pari.[31] Una ricerca successiva offrì più scelte:
- pari
- dispari
- sia pari che dispari
- nessuno dei due
- non lo so
- nessuna risposta
Questa seconda volta, il numero di bambini della stessa fascia di età che rispondevano che lo zero è pari scese al 32%.[32] La percentuale di risposte corrette nel decidere se zero è pari inizialmente sale e poi rimane stabile intorno al 50% dai 7 ai 10 anni.[33] Come paragone, il più facile esercizio di identificare la parità di una sola cifra, aveva una percentuale di successo intorno all'85%.[34]
Nelle interviste, Frobisher stimolava il ragionamento degli studenti. Uno studente del 5º anno (9 anni) aveva deciso che 0 è pari perché si trovava nella tabellina del 2. Uno studente del 4º anno (8 anni) si rese conto che 0 può essere diviso in parti uguali. Un altro studente del 4º anno aveva motivato la parità di 0 dicendo "1 è dispari e se vado giù [0] è pari".[35] In un altro studio Annie Keth osservò una classe di 15 studenti del 2º anno in cui gli studenti si erano convinti l'un l'altro che 0 fosse un numero pari basandosi sull'alternanza fra pari e dispari e sulla possibilità di dividere in due parti uguali un insieme di zero cose.[36]
Idee sbagliate degli studenti sulla parità di zero[modifica | modifica wikitesto]
Le interviste hanno rivelato anche le idee sbagliate che stanno dietro alle risposte errate. Uno studente del secondo anno era "convinto" che lo zero fosse dispari, sulla base del fatto che "è il primo numero da cui si comincia a contare".[37] Uno studente del 4º anno si riferì a zero come a niente e pensava che non fosse né dispari né pari poiché non è un numero.[38]
Ulteriori indagini[modifica | modifica wikitesto]
| Affermazioni fatte dagli studenti[39] |
|---|
| Lo zero non è né pari né dispari. |
| Lo zero potrebbe essere pari. |
| Lo zero non è dispari. |
| Lo zero deve essere pari. |
| Lo zero non è un numero pari. |
| Lo zero sarà sempre un numero pari. |
| Lo zero non sarà sempre un numero pari. |
| Lo zero è pari. |
| Lo zero è speciale. |
Ricerche più approfondite furono condotte da Esther Levenson, Pessia Tsamir e Dina Tirosh, che intervistarono 2 studenti del 6º anno (prima media) che andavano molto bene alle loro lezioni di matematica. Uno studente preferiva utilizzare la teoria per dimostrare le affermazioni matematiche mentre l'altro preferiva utilizzare esempi pratici. Entrambi gli studenti all'inizio pensavano che 0 non fosse né pari né dispari per ragioni differenti. Levenson, Tsamir e Tirosh mostrarono come il ragionamento degli studenti rifletteva i loro concetti di zero e di divisione.[40]
Deborah Loewenberg Ball analizzò le idee di qualche studente appartenente al 3º anno (8 anni) a proposito dei numeri pari, dei numeri dispari e di 0 di cui avevano appena discusso con un gruppo di studenti del quarto anno (9 anni). Gli studenti avevano discusso la parità dello zero, le proprietà dei numeri pari e come venisse fatta la matematica. La questione dello zero assunse varie forme, come si può vedere nella lista qui a destra.[39] Ball e i suoi altri colleghi sostennero che questo episodio dimostrava come gli studenti potessero "fare matematica a scuola", in opposizione alla comune riduzione della disciplina alla risoluzione meccanica di esercizi.
Uno dei temi affrontati più vastamente nella letteratura di ricerca è il disaccordo fra le immagini di concetto della parità e le loro definizioni di concetto.[41] Gli studenti del sesto grado di Levenson et al definivano i numeri pari come "numeri multipli di 2 o numeri divisibili per 2" ma non erano in grado di applicare questa definizione a 0 perché non erano sicuri di come moltiplicare o dividere 0 per due. Il ricercatore alla fine li portò a concludere che 0 fosse pari e gli studenti presero differenti percorsi per arrivare a questa conclusione:
- disegnarono una combinazione di immagini;
- utilizzarono delle definizioni;
- utilizzarono delle spiegazioni pratiche;
- utilizzarono delle spiegazioni teoriche.
In un altro studio, David Dickerson e Damien Pitman esaminarono l'uso delle definizioni di cinque laureandi in matematica. Essi scoprirono che i laureandi erano in gran parte in grado di applicare la definizione di "pari" a 0, ma non erano ancora convinti da questo ragionamento, dal momento che era in conflitto con le loro immagini concettuali.
Conoscenza degli insegnanti[modifica | modifica wikitesto]
Dei ricercatori di didattica della matematica all'Università del Michigan hanno incluso in una loro indagine un quiz vero falso con la seguente domanda "0 è un numero pari?" all'interno di un database di più di 250 domande progettato per misurare la conoscenza dei contenuti delle professoresse. Per loro la domanda rappresentava "cultura generale... che ogni adulto istruito dovrebbe avere"; inoltre considerarono la loro domanda "ideologicamente neutrale", poiché la sua risposta non sarebbe variata fra la matematica insegnata in modo tradizionale e la matematica insegnata con metodi innovativi. In uno studio svolto dal 2000 al 2004 su un campione di 700 professori delle elementari negli Stati Uniti, le performance generali su queste domande prevedettero in maniera significativa i risultati degli studenti in test standardizzati dopo aver partecipato alle lezioni dei professori.[42] In uno studio approfondito svolto nel 2008, dei ricercatori scoprirono una scuola in cui tutti professori insegnavano che 0 non era né dispari né pari, la causa era un professore che aveva fatto da esempio a tutti gli altri. Questo errore concettuale era stato diffuso da un insegnante di matematica nella loro scuola.
Quanti professori hanno idee sbagliate sulla parità di zero?[modifica | modifica wikitesto]
Non è certo quanti professori abbiano conoscenze sbagliate a proposito dello 0 poiché gli studi del Michigan non pubblicarono dati per le domande individuali. Betty Lichtenberg un professore associato di didattica della matematica all'Università della Florida del Sud in uno studio del 1972 riportò che, quando fu dato ad un gruppo di professori delle elementari un quiz vero o falso che includeva la domanda "0 è pari?", essi la considerarono una domanda "tosta" e i due terzi risposero "falso".[43]
Implicazioni nell'istruzione[modifica | modifica wikitesto]
Da un punto di vista puramente matematico, dimostrare che 0 è pari richiede solamente l'applicazione di una definizione, ma nel contesto dell'educazione sono necessarie delle spiegazioni aggiuntive. Un problema riguarda un fondamento della prova la definizione di pari come multiplo intero di 2 non è sempre conosciuta: uno studente nei primi anni dell'istruzione primaria potrebbe non aver ancora imparato cosa significano i termini "intero" o "multiplo" ed è ancora meno probabile che sappiano come moltiplicare per 0.[44] L'affermare una definizione di parità per tutti interi può sembrare una scorciatoia concettuale arbitraria in quanto tutti i numeri pari trovati fino a quel momento erano positivi.
Effetti positivi conseguenti all'insegnare che zero è pari[modifica | modifica wikitesto]
Il fatto che 0 sia pari può aiutare a capire che, mentre il concetto di numero viene esteso dai soli numeri interi positivi a tutti gli interi, includendo 0 e i numeri negativi, anche le proprietà dei numeri come la parità vengono estese in modo non banale.[45]
Cognizione numerica[modifica | modifica wikitesto]

Anche gli adulti che credono che lo 0 sia pari, tuttavia, non sono familiari con questo concetto, fatto che diminuisce il loro tempo di reazione quando devono giudicare se un numero è pari o no. Stanislas Dehaene, un pioniere nel campo della cognizione numerica, ha condotto una serie di esperimenti di questo tipo nei primi anni 1990. Un numero in cifre o in lettere lampeggia su un monitor che un soggetto sta guardando, e un computer registra il tempo necessario al soggetto per premere uno dei due pulsanti per identificare il numero come pari o dispari. I risultati hanno mostrato che per identificare 0 era necessario più tempo che per identificare un qualsiasi altro numero pari. Alcune varianti dell'esperimento hanno trovato ritardi lunghi fino a 60 millisecondi o circa il 10% del tempo di reazione medio - una differenza piccola ma significativa.[47]
Gli esperimenti di Dehaene non erano stati progettati specificamente per indagare la parità dello 0, ma per confrontare modelli concorrenti di come l'informazione di parità venga elaborata ed estratta. Il modello più specifico, l'ipotesi dell'utilizzo del calcolo mentale, suggerisce che la reazione a 0 deve essere veloce; 0 è un numero piccolo, ed è facile calcolare 0 × 2 = 0. (È stato notato che i soggetti dell'esperimento riescono a calcolare e dire il risultato della moltiplicazione per 0 più velocemente del risultato di una moltiplicazione per numeri diversi da 0, anche se sono più lenti a verificare i risultati proposti come 2 × 0 = 0.) I risultati degli esperimenti hanno suggerito che qualcosa di diverso stava accadendo: l'informazione di parità apparentemente era richiamata dalla memoria insieme a un gruppo di proprietà correlate, come l'essere primo o una potenza di due. Sia la sequenza di potenze di 2 che la sequenza dei numeri positivi pari 2, 4, 6, 8,... sono categorie mentali ben distinte, i cui membri sono prototipicamente pari. Lo 0 non appartiene a nessuna lista, quindi le risposte erano più lente.[48]
Ripetuti esperimenti hanno mostrato un ritardo in 0 per soggetti di diversa età, nazione e conoscenze linguistiche, messi a guardare numeri in cifre, detti lettera per lettera e detti lettera per lettera in uno specchio. Il gruppo di Dehaene ha trovato un fattore di differenziazione: la competenza matematica. In uno dei loro esperimenti, gli studenti della École normale supérieure sono stati divisi in due gruppi: quelli impegnati in studi letterari e quelli impegnati a studiare matematica, fisica o biologia. Il rallentamento nel definire la parità dello 0 è stato "trovato sostanzialmente nel primo gruppo [letterario]", e infatti, "prima dell'esperimento, alcuni soggetti [letterari] non erano sicuri se 0 fosse pari o dispari e la sua parità doveva essere ricordata dalla definizione matematica".[49]
Questa forte dipendenza del tempo di risposta con la familiarità mina nuovamente l'ipotesi di calcolo mentale.[50] L'effetto suggerisce anche che non è opportuno includere lo 0 in esperimenti in cui i numeri pari e dispari sono confrontati come gruppo. Come uno studio dice, "La maggior parte dei ricercatori sembrano concordare sul fatto che lo 0 non è un tipico numero pari e non deve essere indagato come parte della linea dei numeri mentale".[51]
Vita di tutti i giorni[modifica | modifica wikitesto]
Alcuni dei contesti in cui la parità dello zero fa la sua apparizione sono puramente retorici. L'argomento fornisce il materiale per bacheche Internet e siti web in cui si chiedono consigli agli esperti.[52] Il linguista Joseph Grimes riflette che chiedere "Zero è pari?" alle coppie sposate è un buon modo per creare disaccordo.[53] Le persone che pensano che lo zero non sia né pari né dispari possono utilizzare la parità di zero come prova che ogni regola ha un controesempio,[54] o come esempio di una domanda trabocchetto.[55]
Intorno al 2000, i media hanno notato un paio di pietre miliari insolite: la data "19/11/1999" è stata l'ultima data del calendario composta solo da cifre dispari che si sarebbe verificata per un tempo molto lungo e che la data "02/02/2000" sarebbe stata la prima data formata da solo cifre pari dopo molto tempo.[56] Poiché questi risultati fanno uso del fatto che 0 è pari, alcuni lettori furono in disaccordo con l'idea.[57]
Nei test standardizzati, se una domanda riguarda il comportamento dei numeri pari, potrebbe essere necessario tenere a mente che 0 è pari.[58] Delle pubblicazioni ufficiali relative al GMAT e al GRE test sia stato che 0 sia pari.[59]
Il fatto che 0 sia pari è rilevante nella suddivisione fra pari e dispari con cui le automobili possono guidare o acquistare la benzina a giorni alterni, secondo la parità dell'ultima cifra nelle loro targhe. Metà dei numeri in un dato intervallo terminano in 0, 2, 4, 6, 8 e l'altra metà in 1, 3, 5, 7, 9, quindi ha senso includere 0 con i numeri pari. Tuttavia, nel 1977, un sistema di razionamento Parigi portò alla confusione. Durante un giorno per soli numeri dispari, la polizia evitò di multare i conducenti le cui targhe terminavano con 0, perché i guidatori non sapevano se 0 fosse pari.[60] Per evitare tale confusione, la legislazione pertinente a volte ribadisce che lo 0 è pari, tali leggi sono state approvate nel Nuovo Galles del Sud[61] e Maryland.[62]
Sulle navi della US Navy, gli scomparti contrassegnati da numeri pari si trovano sul lato sinistro, ma lo zero è riservato per i comparti che intersecano la linea di mezzeria. Cioè, i numeri da sinistra a destra erano nel seguente ordine: 6-4-2-0-1-3-5.[63]
Nel gioco della Roulette, il numero 0 non conta come pari o dispari, dando al Casinò un vantaggio su tali scommesse.[64] Allo stesso modo, la parità di zero può influenzare la percentuale di restituzione nei giochi d'azzardo quando il risultato dipende dal fatto che un certo numero casuale sia pari o dispari e il numero risulta essere uguale a zero.[65]
Anche il gioco del pari o dispari ne è influenzato: se entrambi i giocatori gettano zero dita, il numero totale delle dita è uguale a 0, quindi il giocatore che aveva scelto pari vince.[66] Un manuale per insegnanti suggerisce questo gioco come un modo per introdurre i bambini al concetto che 0 è divisibile per 2.[67]
Reminiscenza filosofica del parimpari, studiato durante il percorso scolastico, potrebbe generare confusione. Nella Scuola pitagorica il parimpari è riferito al numero 1, come elemento di collegamento tra i numeri pari ed i numeri dispari. A diversi anni di distanza dallo studio, il termine parimpari potrebbe essere inteso come sia pari che dispari, o nessuno di questi, ed il numero a cui più facilmente si può associare questo significato è lo 0, distorcendo notevolmente il significato originario. Infatti per i Pitagorici i numeri partivano da 1 e lo zero non esisteva. Infine la Scuola pitagorica considerava il numero uno come numero né pari né dispari, o entrambi, e ciò può aumentare la confusione derivante da uno studio non approfondito e/o non recente:
«Sembra adunque che questi filosofi nel considerare il numero come principio delle cose esistenti ne facciano una causa materiale come proprietà e come modo. Come elementi del numero fissano il pari e il dispari, il primo infinito, l'altro finito. L'uno partecipa di ambedue questi caratteri (essendo insieme pari e dispari). Ogni numero proviene dall'uno e l'intero universo, come già ho detto, è numeri. Altri fra di loro dicono che i principi sono dieci [...]»
Note[modifica | modifica wikitesto]
- ^ Penner, 1999, p. 34: Lemma B.2.2, L'intero 0 è pari e non è dispari. Penner usa il simbolo matematico ∃, il quantificatore di esistenza, per enunciare l'affermazione: "Per dimostrare che 0 sia pari, noi dobbiamo dimostrare che ∃k (0 = 2k), e questo segue dall'uguaglianza 0 = 2 ⋅ 0."
- ^ Ball Lewis Thames, 2008, p. 15 discute questa sfida per le maestre delle elementari, che vogliano dare spiegazioni matematiche per affermazioni matematiche, ma i loro studenti non usano mai le stesse definizioni e non le capiscono quando sono introdotte.
- ^ Compare Lichtenberg, p. 535 Fig. 1
- ^ Lichtenberg, 1972, pp. 535–536 "...i numeri rispondono alla domanda "Quanti?" per gli insiemi di elementi ... zero è il numero che descrive l'insieme vuoto... se gli elementi di ogni insieme sono cancellati a gruppi di 2 [e non rimane niente]... allora il numero di elementi di quell'insieme è un numero pari."
- ^ Lichtenberg, 1972, pp. 535–536 "Zero gruppi di due asterischi sono cerchiati. Non avanzano asterischi. Di conseguenza, lo zero è un numero pari."
- ^ Lichtenberg, 1972, p. 537; vedi Fig. 3. "Se i numeri pari rispondono a un certo criterio... non c'è nessuna ragione per fare un'eccezione per lo zero all'interno di quel criterio."
- ^ Lichtenberg, 1972, pp. 537–538 "A un livello più avanzato ... i numeri espressi come (2 × ▢) + 0 sono numeri pari... zero risponde senza problemi a questa definizione."
- ^ Gowers, 2002, p. 118 "La decisione che può sembrare arbitraria di togliere l'uno dai numeri primi… non esprime nessuna informazione profonda sui numeri: semplicemente è una convenzione utile, adottata in modo che ci sia un unico modo di fattorizzare un qualsiasi numero in primi." Per una discussione più dettagliata, vedi Caldwell, Xiong.
- ^ a b c Partee, 1978, p. xxi.
- ^ a b Stewart, 2001, p. 54 Queste regole sono date, ma non sono citate testualmente.
- ^ Devlin, 1985, pp. 30–33.
- ^ Berlinghoff Grant Skrien, 2001 Per i vertici isolati vedere p. 149; per i gruppi vedere p. 311.
- ^ Lovász Pelikán Vesztergombi, 2003, pp. 127–128.
- ^ Anderson, 2001, p. 53; Hartsfield Ringel, 2003, p. 28
- ^ Lorentz, 1994, pp. 5–6; Lovas Pfenning, 2008, p. 115; Nipkow Paulson Wenzel, 2002, p. 127
- ^ Bunch, 1982, p. 165.
- ^ Salzmann Grundhöfer Hähl Löwen, 2007, p. 168.
- ^ Wise, 2002, pp. 66–67.
- ^ Dummit Foote, 1999, p. 48.
- ^ Andrews, 1990, p. 100.
- ^ Tabachnikova Smith, 2000, p. 99; Anderson Feil, 2005, pp. 437–438
- ^ Barbeau, 2003, p. 98.
- ^ Arnold, 1919, p. 21 "Secondo lo stesso test lo zero sorpassa tutti gli altri numeri in 'Parità'.'"; Wong, 1997, p. 479 "Di conseguenza, l'intero b000⋯000 = 0 è 'il più pari.'
- ^ Wong, 1997, p. 479.
- ^ Gouvêa, 1997, p. 25 Per un primo generico p: "Il ragionamento qui è che possiamo ovviamente dividere 0 per p, il risultato è 0, che possiamo dividere per p, e il risultato è 0, che possiamo dividere per p...(ellissi nell'originale)".
- ^ Krantz, 2001, p. 4.
- ^ Salzmann Grundhöfer Hähl Löwen, 2007, p. 224.
- ^ a b Frobisher, 1999, p. 41.
- ^ Questo è vero negli Stati Uniti D'America, in Canada, in Gran Bretagna, in Australia, e in Israele; vediLevenson, Tsamir.
- ^ Frobisher, 1999, pp. 31 (Introduzione); 40–41 (Il numero zero); 48 (Implicazioni per l'insegnamento).
- ^ Frobisher, 1999, pp. 37, 40, 42; i risultati provengono da un'indagine condotta a metà della sessione estiva del 1992.
- ^ Frobisher, 1999, p. 41 "La percentuale di bambini del 2º anno che sceglievano che zero è un numero pari è molto più bassa che nel precedente studio, 32% rispetto al 45%"
- ^ Frobisher, 1999, p. 41 "Il successo nel decidere se zero è pari o no non continua a crescere con l'età, con circa un bambino su due, tra i 6 e gli 11 anni, che mette la crocetta nella casella 'pari'..."
- ^ Frobisher, 1999, pp. 40–42, 47; questi risultati derivano da uno studio effettuato nel febbraio del 1999, su 481 bambini, provenienti da tre scuole differenti con differenti livelli di apprendimento.
- ^ Frobisher, 1999, p. 41, attribuito a "Jonathan"
- ^ Keith, 2006, pp. 35–68 "C'era un piccolo disaccordo sull'idea che zero fosse un numero pari. Gli studenti convinsero i pochi che non erano d'accordo con due argomentazioni. La prima era che i numeri seguono uno schema ...dispari, pari, dispari, pari, dispari, pari... e poiché due è pari e uno è dispari il numero prima di uno, che non sia una frazione, sarebbe zero. Dunque zero dev'essere pari. La seconda argomentazione era che se una persona ha zero cose e le divide in due parti uguali allora ce ne sarebbero zero in ogni gruppo. I due gruppi avrebbero lo stesso numero di oggetti: zero."
- ^ Frobisher, 1999, p. 41, attribuito a "Joseph"
- ^ Frobisher, 1999, p. 41, attribuito a "Richard"
- ^ a b Ball Lewis Thames, 2008, p. 27, Figura 1.5 "Affermazioni matematiche sullo zero."
- ^ Levenson Tsamir Tirosh, 2007, pp. 83–95.
- ^ Levenson Tsamir Tirosh, 2007; Dickerson Pitman, 2012
- ^ Ball Hill Bass, 2005, pp. 14–16.
- ^ Lichtenberg, 1972, p. 535.
- ^ Ball Lewis Thames, 2008, p. 15. Vedi anche l'introduzione di Ball per una discussione sulle definizioni appropriate.
- ^ Come concluso da Levenson, Tsamir, citando Freudenthal, p. 460
- ^ Nuerk, Iversen: "Si può osservare che zero differisce fortemente da tutti gli altri numeri indipendentemente dalla mano usata per rispondere. (Vedere la linea che separa zero dagli altri numeri.)"
- ^ Vedi i dati in Dehaene, Bossini, e riassunti da Nuerk, Iversen.
- ^ Dehaene Bossini Giraux, 1993, pp. 374–376.
- ^ Dehaene Bossini Giraux, 1993, pp. 376–377.
- ^ Dehaene Bossini Giraux, 1993, p. 376 "In un qualche senso intuitivo, la nozione di parità è familiare solo per i numeri più grandi di 2. Infatti, prima dell'esperimento, dei soggetti [L] non erano certi sul fatto che 0 fosse pari o dispari e lo [che è pari] hanno dovuto ricavare dalla definizione di pari. La prova, in breve, suggerisce che [la parità] invece di essere calcolata sul momento usando il criterio di divisibilità per due, l'informazione di parità è presa dalla memoria insieme a un numero e alle sue altre proprietà... Se si accede a una memoria semantica quando si decide se un numero è pari o dispari, allora le differenze fra gli individui dovrebbero essere trovate a seconda della familiarità dei soggetti con i concetti dei numeri."
- ^ Nuerk Iversen Willmes, 2004, pp. 838, 860–861.
- ^ The Math Forum participants, 2000; Straight Dope Science Advisory Board, 1999; Doctor Rick, 2001
- ^ Grimes, 1975, p. 156 "...uno può porre questa domanda a una coppia sposata di propria volontà (1) Lo zero è pari?... Molte coppie non sono d'accordo..."
- ^ Wilden Hammer, 1987, p. 104.
- ^ Snow, 2001; Morgan, 2001
- ^ Steinberg, 1999; Siegel, 1999; Stingl, 2006
- ^ Sones Sones, 2002 "Segue che zero è pari e che 2/20/2000 risolve senza problemi il 'mistero'. Sì, è sempre sorprendente quante persone sono infastidite dal dire che zero è pari..."; Column 8 readers, 2006a "'...secondo i matematici, il numero zero, insieme ai numeri negativi e alle frazioni, non è né pari né dispari,' scrive Etan..."; Column 8 readers, 2006b "'Io sono d'accordo sul fatto che zero sia pari, ma il Professor Bunder lo vuole 'dimostrare' affermando che 0 = 2 x 0? Secondo questa logica (da un 'laureato' in logica matematica, niente meno), poiché 0 = 1 x 0, 0 è anche dispari!' Il professore controbatterà a questo, logicamente, egli ha delle motivazioni sensate per farlo, ma forse noi stiamo considerando questo argomento un po' troppo alla leggera..."
- ^ Kaplan Staff, 2004, p. 227.
- ^ Graduate Management Admission Council, 2005, pp. 108, 295–297; Educational Testing Service, 2009, p. 1
- ^ Arsham, 2002; Questa affermazione è attribuita al broadcast heute del primo di ottobre, 1977. Il racconto di Arsham è ripetuto da Crumpacker, p. 165.
- ^ Sones Sones, 2002 "Il matematico di stato Penn George Andrews, che si riferisce a un partizionamento del gas in Australia... Poi qualcuno nel parlamento del Nuovo Galles del Sud affermò che in questo razionamento le targhe terminanti in zero non avrebbero mai potuto ottenere del gas, perché 'zero non è né dispari né pari'. Quindi il parlamento del Nuovo Galles del Sud emise una legge per cui inerentemente al razionamento del gas, lo zero è pari!'"
- ^ Una specifica di legge del 1980 in Maryland, "(a)Nei giorni pari la benzina potrà essere comprata solo dai guidatori i cui veicoli con targhe personalizzate non hanno numeri o i cui veicoli le cui targhe standard terminano con numeri pari. Questo non deve includere le targhe dei radioamatori. Lo zero è pari; (b) Nei giorni dispari..." quotazione parziale presa da Department of Legislative Reference, Laws of the State of Maryland, Volume 2, 1974, p. 3236. URL consultato il 2 giugno 2013.
- ^ Cutler, 2008, pp. 237–238.
- ^ Brisman, 2004, p. 153.
- ^ Smock, 2006; Hohmann, 2007; Turner, 1996
- ^ Diagram Group, 1983, p. 213.
- ^ Baroody Coslick, 1998, p. 1.33.
- ^ Citato in Pier Michele Giordano, I presocratici, Edizioni ARS G. L., Vercelli 1996, pp. 103-104.
Bibliografia[modifica | modifica wikitesto]
- Ian Anderson, A First Course in Discrete Mathematics, London, Springer, 2001, ISBN 1-85233-236-0.
- Marlow Anderson e Todd Feil, A First Course in Abstract Algebra: Rings, Groups, And Fields, London, CRC Press, 2005, ISBN 1-58488-515-7.
- Edna Andrews, Markedness Theory: the union of asymmetry and semiosis in language, Durham, Duke University Press, 1990, ISBN 0-8223-0959-9.
- C. L. Arnold, The Number Zero, in The Ohio Educational Monthly, vol. 68, n. 1, gennaio 1919, pp. 21-22. URL consultato l'11 aprile 2010.
- Hossein Arsham, Zero in Four Dimensions: Historical, Psychological, Cultural, and Logical Perspectives, The Pantaneto Forum, gennaio 2002. URL consultato il 24 settembre 2007 (archiviato dall'url originale il 25 settembre 2007).
- Deborah Loewenberg Ball, Heather C. Hill e Hyman Bass, Knowing Mathematics for Teaching: Who Knows Mathematics Well Enough To Teach Third Grade, and How Can We Decide? (PDF), in American Educator, 2005. URL consultato il 16 settembre 2007.
- Deborah Loewenberg Ball, Jennifer Lewis e Mark Hoover Thames, Making mathematics work in school (PDF), in Journal for Research in Mathematics Education, M14, 2008, pp. 13–44 and 195–200. URL consultato il 4 marzo 2010.
- Edward Joseph Barbeau, Polynomials, Springer, 2003, ISBN 0-387-40627-1.
- Arthur Baroody e Ronald Coslick, Fostering Children's Mathematical Power: An Investigative Approach to K-8, Lawrence Erlbaum Associates, 1998, ISBN 0-8058-3105-3.
- William P. Berlinghoff, Kerry E. Grant e Dale Skrien, A Mathematics Sampler: Topics for the Liberal Arts, 5th rev., Rowman & Littlefield, 2001, ISBN 0-7425-0202-3.
- Kim C. Border, Fixed Point Theorems with Applications to Economics and Game Theory, Cambridge University Press, 1985, ISBN 0-521-38808-2.
- Andrew Brisman, Mensa Guide to Casino Gambling: Winning Ways, Sterling, 2004, ISBN 1-4027-1300-2.
- Bryan H. Bunch, Mathematical Fallacies and Paradoxes, Van Nostrand Reinhold, 1982, ISBN 0-442-24905-5.
- Chris K. Caldwell e Yeng Xiong, What is the Smallest Prime?, in Journal of Integer Sequences, vol. 15, n. 9, 27 dicembre 2012, arXiv:1209.2007.
- Column 8 readers, Column 8, The Sydney Morning Herald, First, 10 marzo 2006, p. 18.
- Column 8 readers, Column 8, The Sydney Morning Herald, First, 16 marzo 2006, p. 20.
- Bunny Crumpacker, Perfect Figures: The Lore of Numbers and How We Learned to Count, Macmillan, 2007, ISBN 0-312-36005-3.
- Thomas J. Cutler, The Bluejacket's Manual: United States Navy, Centennial, Naval Institute Press, 2008, ISBN 1-55750-221-8.
- Stanislas Dehaene, Serge Bossini e Pascal Giraux, The mental representation of parity and numerical magnitude (PDF), in Journal of Experimental Psychology: General, vol. 122, n. 3, 1993, pp. 371-396, DOI:10.1037/0096-3445.122.3.371. URL consultato il 13 settembre 2007 (archiviato dall'url originale il 19 luglio 2011).
- Keith Devlin, The golden age of mathematics, in New Scientist, vol. 106, n. 1452, aprile 1985.
- Diagram Group, The Official World Encyclopedia of Sports and Games, Paddington Press, 1983, ISBN 0-448-22202-7.
- David S Dickerson e Damien J Pitman, Advanced college-level students' categorization and use of mathematical definitions (PDF), in Tai-Yih Tso (a cura di), Proceedings of the 36th Conference of the International Group for the Psychology of Mathematics Education, vol. 2, luglio 2012, pp. 187-195 (archiviato dall'url originale il 18 dicembre 2013).
- David S. Dummit e Richard M. Foote, Abstract Algebra, 2e, New York, Wiley, 1999, ISBN 0-471-36857-1.
- Educational Testing Service, Mathematical Conventions for the Quantitative Reasoning Measure of the GRE® revised General Test (PDF), Educational Testing Service, 2009. URL consultato il 6 settembre 2011.
- H. Freudenthal, Didactical phenomenology of mathematical structures, Dordrecht, The Netherlands, Reidel, 1983.
- Len Frobisher, Primary School Children's Knowledge of Odd and Even Numbers, in Anthony Orton (a cura di), Pattern in the Teaching and Learning of Mathematics, London, Cassell, 1999, pp. 31-48.
- Fernando Quadros Gouvêa, p-adic numbers: an introduction, 2nd, Springer-Verlag, 1997, ISBN 3-540-62911-4.
- Timothy Gowers, Mathematics: A Very Short Introduction, Oxford University Press, 2002, ISBN 978-0-19-285361-5.
- Graduate Management Admission Council, The Official Guide for GMAT Review, 11th, McLean, VA, Graduate Management Admission Council, settembre 2005, ISBN 0-9765709-0-4.
- Joseph E. Grimes, The Thread of Discourse, Walter de Gruyter, 1975, ISBN 90-279-3164-X.
- Nora Hartsfield e Gerhard Ringel, Pearls in Graph Theory: A Comprehensive Introduction, Mineola, Courier Dover, 2003, ISBN 0-486-43232-7.
- Heather C. Hill, Merrie L. Blunk, Charalambos Y. Charalambous, Jennifer M. Lewis, Geoffrey C. Phelps, Laurie Sleep e Deborah Loewenberg Ball, Mathematical Knowledge for Teaching and the Mathematical Quality of Instruction: An Exploratory Study, in Cognition and Instruction, vol. 26, n. 4, 2008, pp. 430-511, DOI:10.1080/07370000802177235.
- George Hohmann, Companies let market determine new name, Charleston Gazette, 25 ottobre 2007, p. P1C, Template:Factiva.
- Kaplan Staff, Kaplan SAT 2400, 2005 Edition, Simon and Schuster, 2004, ISBN 0-7432-6035-X.
- Annie Keith, Mathematical Argument in a Second Grade Class: Generating and Justifying Generalized Statements about Odd and Even Numbers, in Teachers Engaged in Research: Inquiry in Mathematics Classrooms, Grades Pre-K-2, IAP, 2006, ISBN 1-59311-495-8.
- Steven George Krantz, Dictionary of algebra, arithmetic, and trigonometry, CRC Press, 2001, ISBN 1-58488-052-X.
- Esther Levenson, Pessia Tsamir e Dina Tirosh, Neither even nor odd: Sixth grade students' dilemmas regarding the parity of zero, in The Journal of Mathematical Behavior, vol. 26, n. 2, 2007, pp. 83-95, DOI:10.1016/j.jmathb.2007.05.004.
- Betty Plunkett Lichtenberg, Zero is an even number, in The Arithmetic Teacher, vol. 19, n. 7, novembre 1972, pp. 535-538.
- Richard J. Lorentz, Recursive Algorithms, Intellect Books, 1994, ISBN 1-56750-037-4.
- William Lovas e Frank Pfenning, A Bidirectional Refinement Type System for LF, in Electronic Notes in Theoretical Computer Science, vol. 196, 22 gennaio 2008, pp. 113-128, DOI:10.1016/j.entcs.2007.09.021. URL consultato il 16 giugno 2012.
- László Lovász, József Pelikán e Katalin L. Vesztergombi, Discrete Mathematics: Elementary and Beyond, Springer, 2003, ISBN 0-387-95585-2.
- Frank Morgan, Old Coins, Frank Morgan's Math Chat, The Mathematical Association of America, 5 aprile 2001. URL consultato il 22 agosto 2009.
- Tobias Nipkow, Lawrence C. Paulson e Markus Wenzel, Isabelle/Hol: A Proof Assistant for Higher-Order Logic, Springer, 2002, ISBN 3-540-43376-7.
- Hans-Christoph Nuerk, Wiebke Iversen e Klaus Willmes, Notational modulation of the SNARC and the MARC (linguistic markedness of response codes) effect, in The Quarterly Journal of Experimental Psychology A, vol. 57, n. 5, luglio 2004, pp. 835-863, DOI:10.1080/02724980343000512.
- Barbara Hall Partee, Fundamentals of Mathematics for Linguistics, Dordrecht, D. Reidel, 1978, ISBN 90-277-0809-6.
- Robert C. Penner, Discrete Mathematics: Proof Techniques and Mathematical Structures, River Edje, World Scientific, 1999, ISBN 981-02-4088-0.
- H. Salzmann, T. Grundhöfer, H. Hähl e R. Löwen, The Classical Fields: Structural Features of the Real and Rational Numbers, Cambridge University Press, 2007, ISBN 0-521-86516-6.
- Robert Siegel, Analysis: Today's date, November 19th, 1999, contains all odd numbers; the next even-numbered date will be February 2nd, 2000, All Things Considered, National Public Radio, 19 novembre 1999, Template:Factiva.
- Doug Smock, The odd bets: Hines Ward vs. Tiger Woods, Charleston Gazette, 6 febbraio 2006, p. P1B, Template:Factiva.
- Tony Snow, Bubba's fools, Jewish World Review, 23 febbraio 2001. URL consultato il 22 agosto 2009.
- Bill Sones e Rich Sones, To hide your age, button your lips, Deseret News, 8 maggio 2002, p. C07, Template:Factiva.
- Ross M. Starr, General Equilibrium Theory: An Introduction, Cambridge University Press, 1997, ISBN 0-521-56473-5.
- Neil Steinberg, Even year, odd facts, Chicago Sun-Times, 5XS, 30 novembre 1999, p. 50, Template:Factiva.
- Mark Alan Stewart, 30 Days to the GMAT CAT, Stamford, Thomson, 2001, ISBN 0-7689-0635-0.
- Jim Stingl, 01:02:03 04/05/06; We can count on some things in life, Milwaukee Journal Sentinel, Final, 5 aprile 2006, p. B1, Template:Factiva.
- Olga M. Tabachnikova e Geoff C. Smith, Topics in Group Theory, London, Springer, 2000, ISBN 1-85233-235-2.
- The Math Forum participants, A question around zero, Math Forum » Discussions » History » Historia-Matematica, Drexel University, 2000. URL consultato il 25 settembre 2007.
- Julian Turner, Sports Betting – For Lytham Look to the South Pacific, The Guardian, 13 luglio 1996, p. 23, Template:Factiva.
- Anthony Wilden e Rhonda Hammer, The rules are no game: the strategy of communication, Routledge Kegan & Paul, 1987, ISBN 0-7100-9868-5.
- Stephen Wise, GIS Basics, CRC Press, 2002, ISBN 0-415-24651-2.
- Samuel Shaw Ming Wong, Computational Methods in Physics and Engineering, World Scientific, 1997, ISBN 981-02-3043-5.
Altri progetti[modifica | modifica wikitesto]
 Wikimedia Commons contiene immagini o altri file sulla parità dello zero
Wikimedia Commons contiene immagini o altri file sulla parità dello zero
Collegamenti esterni[modifica | modifica wikitesto]
- Doctor Rick, Is Zero Even?, Ask Dr. Math, The Math Forum, 2001. URL consultato il 6 giugno 2013.
- Straight Dope Science Advisory Board, Is zero odd or even?, The Straight Dope Mailbag, 1999. URL consultato il 6 giugno 2013.
- Is Zero Even? - Numberphile, video with Dr. James Grime, University of Nottingham