Onda sinusoidale

In fisica, un'onda sinusoidale è un'onda descritta matematicamente dalla funzione seno. Una sinusoide o curva sinusoidale è la curva rappresentata dal grafico del seno. Una sinusoide è analoga alla curva relativa alla funzione coseno, detta cosinusoide, sfasata di .
Definizione[modifica | modifica wikitesto]
Un'onda sinusoidale è un'onda dove la variabile è una funzione della forma:
dove è l'ampiezza, mentre:
è la pulsazione (o velocità angolare, indica quanti periodi ci sono in un intervallo di ). Inoltre:
è la frequenza, che indica quante volte in un'unità di tempo la funzione si ripete, e:
è il periodo, con oppure la fase.
Il grafico di una tale classe di funzioni è compreso tra le rette e .
Poiché si tratta di una funzione periodica, detto il periodo si ha:
Caratteristiche[modifica | modifica wikitesto]

Usando la formula di Eulero, un'onda sinusoidale può essere rappresentata come la parte reale della funzione:
dove è il vettore d'onda, che identifica la direzione di propagazione dell'onda al posto della velocità di propagazione. Il suo modulo è chiamato pulsazione spaziale, ed è legato alla lunghezza d'onda dalla relazione:
Lo scalare è l'ampiezza dell'onda, e rappresenta il massimo valore della grandezza rappresentativa dell'onda in un periodo. Il termine rappresenta la fase iniziale dell'onda.
Le onde sinusoidali sono una soluzione particolare dell'equazione delle onde. L'onda è una funzione dello spazio e tempo, per cui un'onda monodimensionale associa ad ogni posizione spaziale e ad ogni tempo un'ampiezza di oscillazione attorno alla posizione di equilibrio:
Sono possibili perciò due punti di vista:
- Scegliendo di valutare la dimensione temporale ( è fissato), si esprime l'oscillazione in dipendenza dal tempo come .
- Scegliendo di focalizzare l'attenzione sullo stato di un mezzo perturbato in un certo istante ( è fissato) si ha l'"istantanea" dell'onda, cioè la forma d'onda (il suo profilo al tempo fissato di osservazione). L'oscillazione può essere espressa in funzione della posizione come .
In entrambi i casi si può partire dalla dipendenza co-sinusoidale delle variabili nel moto armonico, ricavate considerando quest'ultimo come un'opportuna proiezione di un moto circolare uniforme:
dove è l'ampiezza dell'oscillazione e è la fase iniziale. Attribuendo a un valore di 90 gradi si può passare da una forma in coseno a una in seno, quindi le espressioni sono equivalenti. L'espressione è in per attuare la "visualizzazione" dell'oscillazione lungo l'asse verticale del sistema coordinato.
Fissando la variabile si ha:
dove è il periodo dell'onda. La fase iniziale è nulla, e se la perturbazione sul mezzo si propaga dall'inizio muovendosi con velocità di fase allora essa raggiungerà un altro punto (a destra dell'origine) a una certa distanza dopo un tempo:
Ciò significa che il punto alla coordinata avrà, al tempo , uno spostamento verticale uguale a quello che aveva il punto iniziale t1 secondi prima. La propagazione è quindi descritta dall'espressione:
Raccogliendo si può passare a una forma più comune che talvolta si trova sui testi:
Se si chiama numero d'onda la quantità , e se la pulsazione è , il rapporto già noto dallo studio del moto circolare consente di pervenire formalmente all'equazione delle onde armoniche:
Se all'espressione in coseno iniziale si fosse aggiunta una fase di 90° si sarebbe ottenuta un'espressione in seno negativo poiché , e questo avrebbe portato a un'espressione sinusoidale con i segni interni invertiti, cioè , che talvolta viene presentata sui testi.
Considerando il secondo caso dell'elenco sopra, ad un tempo fissato:

Si è espresso il tempo come , sostituendo e usando la relazione fondamentale delle onde (la lunghezza d'onda è lo spazio percorso da un'onda con velocità di fase in un periodo ): in ogni caso, quel che conta è che si ottiene una cosinusoide di periodo spaziale dipendente solo dalla posizione . Se l'impulso si sta muovendo lungo l'asse delle ascisse, inducendo un'oscillazione sulle ordinate, ad un certo istante successivo a quello fissato il punto alla certa coordinata avrà un'elevazione uguale a quella del punto da cui l'impulso è partito secondi prima. L'onda si propaga quindi (verso destra) con un profilo dato da:
mentre si sarebbe dovuta considerare un'espressione in parentesi tonda del tipo se si fosse voluta descrivere la propagazione verso sinistra. Esprimendo e sostituendo, si ha l'espressione:
che considerando la relazione goniometrica è analoga a quella ottenuta in precedenza (perché si cambiano i segni dell'argomento).
-
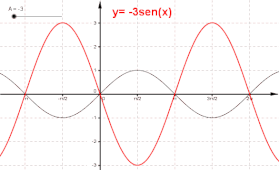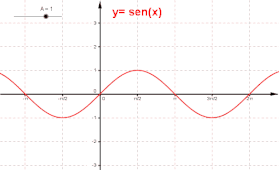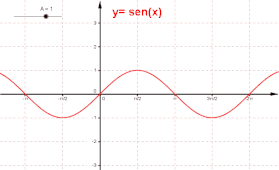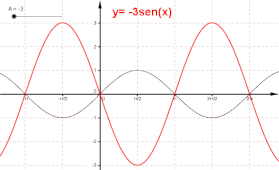
Il parametro A (Ampiezza) provoca una dilatazione lungo l'asse y
-
Il parametro (pulsazione) provoca una dilatazione lungo l'asse x
-
Il parametro (fase) provoca una traslazione orizzontale
-
Il parametro k provoca una traslazione verticale
Bibliografia[modifica | modifica wikitesto]
- (EN) M. Abramowitz, I.A. Stegun, "Handbook of mathematical functions" , Dover, reprint (1972) pp. §4.3
Voci correlate[modifica | modifica wikitesto]
Altri progetti[modifica | modifica wikitesto]
 Wikimedia Commons contiene immagini o altri file sull'onda sinusoidale
Wikimedia Commons contiene immagini o altri file sull'onda sinusoidale
Collegamenti esterni[modifica | modifica wikitesto]
- (EN) Yu.A. Gor'kov, Sinusoid, in Encyclopaedia of Mathematics, Springer e European Mathematical Society, 2002.
- (EN) Yu.A. Gor'kov, Sine, in Encyclopaedia of Mathematics, Springer e European Mathematical Society, 2002.














![{\displaystyle f(\xi )=f_{\max }\,\Re {\left[\mathrm {e} ^{i({\vec {k}}\cdot {\vec {r}}+\omega t+\phi )}\right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c01a684646168eae054e8e6e0edec704e356495)















![{\displaystyle y=y_{\max }\,\cos \left[{\frac {2\pi }{\tau }}(t-t1)\right]=y_{\max }\,\cos \left[{\frac {2\pi }{\tau }}\left(t-{\frac {x}{v}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e5c1431858ee6a73bc5b07a034af20d76941167)
![{\displaystyle y=y_{\max }\,\cos \left[2\pi \left({\frac {t}{\tau }}-{\frac {x}{\lambda }}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9995c42c3d0c6118fb2e5959f265253f97c7d5b8)








![{\displaystyle y=\sin \left[2\pi \left({\frac {x}{2\pi }}-{\frac {t}{2\pi }}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ef0273363022869b60c8a806cd66e00bd945ec8)





![{\displaystyle y=y_{\max }\,\cos \left[{\frac {2\pi }{\lambda }}(x-vt)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4b00f672aa842a19aa259c9ec1949b7246a5e77)


![{\displaystyle y=y_{\max }\,\cos \left[2\pi \left({\frac {x}{\lambda }}-{\frac {t}{\tau }}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08dbd6d9af37e6212eb1e3108af54083a22b6df5)