Accuratezza
Nella teoria degli errori, l'accuratezza è il grado di corrispondenza del dato teorico, desumibile da una serie di valori misurati (campione di dati), con il dato reale o di riferimento, ovvero la differenza tra valore medio campionario e valore vero o di riferimento. Indica la vicinanza del valore trovato a quello reale. È un concetto qualitativo che dipende sia dagli errori casuali che da quelli sistematici.
In passato, specie nel mondo anglosassone o nell'ambiente elettrico-elettronico, il termine accuratezza era sinonimo di precisione. Nella moderna metrologia i due termini invece indicano concetti differenti, e l'accostamento deve essere pertanto evitato. La precisione di una misurazione è, infatti, una connotazione globale non direttamente quantificabile. È riferibile, invece, più correttamente, a due aspetti quantificabili di quella misurazione: la accuratezza e la ripetibilità di quella misura.
Concetto d'accuratezza[modifica | modifica wikitesto]
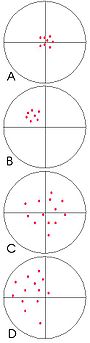
Per chiarire il concetto, si faccia riferimento ad una nota analogia con una serie di frecce scagliate su un bersaglio: più la serie di frecce tende a colpire il centro del bersaglio, più questa si definisce accurata. Nell'immagine a destra, gli esempi A e C rappresentano due rosate accurate, in quanto tutte e due tendono "mediamente" verso il centro del bersaglio.
Come si nota, mentre la rosata "A" si presenta circoscritta intorno al centro, la rosata "C" si presenta dispersa su una larga superficie. La dispersione della serie di frecce non incide sull'accuratezza (ovvero la "tendenza" delle frecce ad andare verso il centro cioè verso il valore medio di riferimento), ma è definibile in termini di scarsa ripetibilità dei risultati dei tiri (varianza dei tiri).
La rosata B, pur essendo ripetibile, non si presenta accurata, in quanto non tende a colpire il centro del bersaglio. Lo scostamento del tiro, costante e ripetibile, evidenzia invece un errore sistematico nel lancio delle frecce rispetto al valore medio di riferimento cioè il centro del bersaglio. Le misure possono però dirsi ripetibili o a varianza bassa (impropriamente: 'più precise') rispetto al loro valore medio campionario.
L'esempio D mostra infine il caso peggiore, in cui i risultati non sono né accurati né ripetibili.
Nelle scienze militari, il concetto di accuratezza viene impiegato tecnicamente anche per indicare l'accuratezza di fuoco. Questo misura la precisione di fuoco espressa dalla vicinanza di un insieme di tiri diretti al bersaglio e attorno ad esso, rispetto a quelli fuori bersaglio[1].
Accuratezza della misura[modifica | modifica wikitesto]
In accordo con concetto generale, l'accuratezza della misura è il grado di concordanza tra il valore medio desunto attraverso una o più misure e il relativo valore vero cioè il valore assunto come riferimento.
L'errore che deriva dallo scostamento tra il valore misurato e il valore vero è chiamato errore d'accuratezza (o semplicemente accuratezza) e, come già accennato, normalmente non è un contributo nella valutazione dell'incertezza di misura (si veda più avanti per il caso degli strumenti). Comunemente questo errore è espresso come:
- dove:
- = errore d'accuratezza
- = valore misurato
- = valore vero
Nel caso più semplice, il valore misurato è il valore ottenuto da una singola misura; altrimenti, specie dove si sospetta l'esistenza di fonti di errori casuali significativi, è la media di una serie di misure fatte mantenendo le medesime condizioni.
Relatività dell'accuratezza[modifica | modifica wikitesto]
Bisogna notare che il valore vero è un valore convenzionale, tanto più che nessun valore può essere perfettamente noto. Il valore vero, pur essendo convenzionale, è dedotto da misure effettuate con strumenti molto precisi, cioè strumenti i cui valori misurati, di una stessa grandezza fisica, si discostano molto poco fra loro. Ad esempio, non assumeremmo mai come valore vero della massa di un oggetto, il valore medio misurato con una bilancia che ha fornito un set di misure del genere: 20,3 g; 25,4 g 32,5g 27,9 g. Al contrario il valore medio della stessa grandezza, misurato con una bilancia che ha fornito quest'altro set di misure:" 20,3 g; 20,2 g; 20,1 g ; 20,2 g può ragionevolmente essere assunto come valore vero. Ne consegue che il concetto d'accuratezza va sempre messo in relazione al valore-vero che gli operatori considerano "giusto", per scelta, dove tale scelta è motivata dalla precisione dello strumento con cui è stato ottenuto quel valore: la precisione è oggettiva non soggettiva.
Esempio:
- Supponiamo di voler verificare l'accuratezza di misura di una bilancia usando un peso campione da 1 kg.
- Posando il peso campione sul piatto della bilancia, potremmo leggere una misura di 1,0001 kg. Siccome il peso "giusto" è considerato il peso nominale del campione, potremmo dedurre che l'accuratezza della bilancia è di 0,1 g.
- D'altronde potremmo disporre di un peso campione di classe "M2" e, analizzando il rapporto di taratura di quest'ultimo, scoprire che il peso reale del campione è proprio 1,0001 kg (il valore rientra nella classe di precisione citata). In tal caso si può dedurre che la bilancia sia assolutamente accurata, con la precisione limitata esclusivamente dalla sua risoluzione e dall'incertezza di misura del campione.
In questo caso, se è considerato "vero" il valore nominale del peso, lo strumento risulta inaccurato; ma se invece è considerato "vero" il valore del rapporto di taratura, lo stesso strumento risulta molto accurato. Ciò è possibile in quanto, facendo un'analisi più approfondita, si è potuto cambiare il "valore convenzionalmente vero" usato come riferimento.
Correzione degli errori d'accuratezza[modifica | modifica wikitesto]
Come si è accennato, la presenza d'errori costanti che "spostano" le letture reali dal valore vero, indicano l'esistenza di fonti di errori sistematici.
Una volta riconosciuti e adeguatamente caratterizzati, gli errori sistematici possono essere corretti agendo sul valore misurato. Riprendendo l'esempio precedente, se la bilancia in taratura presentasse a tutti i pesi campione usati una lettura superiore dello 0,01 %, si potrebbe pensare di correggere a posteriori tutte le misure da essa effettuata, annullando l'errore d'accuratezza.
Un altro sistema per correggere gli errori d'accuratezza è quello di agire a priori, calibrando opportunamente la strumentazione di misura o eliminando fisicamente le fonti d'errore sistematico.
Accuratezza strumentale[modifica | modifica wikitesto]
Si definisce accuratezza strumentale l'attitudine di uno strumento di misura a dare indicazioni prive d'errori sistematici, e tendenti al valore vero del misurando,
Uno strumento deteriorato o alterato, usato per acquisire una serie di valori, potrebbe apparire preciso in quanto i valori ottenuti potrebbero essere vicini tra loro, ma essere scarsamente accurato se questi valori differiscono dal valore reale del misurando. Si pensi per esempio, ad un metro impiegato ad una temperatura ambientale elevata e quindi allungatosi a causa della dilatazione termica.
La valutazione dell'accuratezza strumentale viene fatta tarando lo strumento tramite opportuni campioni. Per il calcolo dell'errore d'accuratezza valgono le indicazioni generali riportate nel paragrafo precedente.
Accuratezza strumentale e incertezza di misura[modifica | modifica wikitesto]
Come detto in precedenza, gli errori sistematici per loro natura possono essere corretti, e pertanto l'errore d'accuratezza non dovrebbe influire sull'incertezza di misura.
Nella pratica però spesso la correzione degli errori d'accuratezza su strumenti di misura:
- non è facilmente realizzabile;
- pur teoricamente realizzabile, non è conveniente per l'uso che si fa dello strumento;
- risulta troppo lunga o macchinosa date le necessità applicative.
In questo modo l'utilizzatore finisce per considerare come "vero" il valore direttamente letto sullo strumento, corretto o meno. In tal caso, l'errore d'accuratezza finisce a tutti gli effetti per peggiorare la precisione di misura, o in termini metrologici: aumentare l'incertezza di misura strumentale.
In pratica, all'incertezza di misura dovuta agli altri errori non correggibili (risoluzione, ripetibilità, incertezza dei campioni, ecc.) si somma anche l'incertezza che deriva dalla mancata correzione degli errori sistematici. Pertanto, in linea di massima:
- ,
- dove:
- = incertezza di misura dello strumento
- = errore d'accuratezza
- = altri contributi d'incertezza
Esempio: un operatore raramente si porrà il problema di correggere dagli errori d'accuratezza le letture effettuate su un manometro. Normalmente per praticità, farà una misura e considererà "vero" il valore letto. Per dare un senso alla misura, bisognerà così sommare all'incertezza dovuta agli errori non correggibili, anche il massimo errore d'accuratezza rilevato dalla taratura.
Questo è un problema comune a molti sistemi di misura a lettura diretta (indicatori digitali, voltmetri, ecc.): il vantaggio di questi strumenti sta nella praticità della lettura, che non si vuole ovviamente annullare con la necessità di complicate correzioni sulle misure. Si finisce così per pagarlo con un aumento dell'incertezza strumentale.
Approccio statistico[modifica | modifica wikitesto]
Con la pubblicazione della norma ISO GUM (Guide Uncertainty Measurement), introdotta in Italia con la norma UNI CEI ENV 13005 "Guida all'espressione dell'incertezza di misura", e la diffusione dell'approccio statistico nella determinazione dell'incertezza di misura, è nata la necessità d'integrare (dove necessario) il contributo all'incertezza dovuta agli errori d'accuratezza non corretti.
Oggi diverse norme e raccomandazioni cercano di uniformare le valutazioni dei contributi d'incertezza, almeno per tipologia di strumenti. Ma a tutt'oggi, presso gli organi di normazione o presso chi si occupa attivamente del calcolo dell'incertezza di misura, vi è ancora discussione di come effettuare l'integrazione tra contributi derivanti da errori casuali e quelli derivanti da errori sistematici.
Un metodo semplice, anche se forse troppo conservativo, è valutare il contributo d'incertezza pari al massimo errore d'accuratezza (rilevato da una serie di misure) diviso radice 3; cioè:
- dove:
- = massimo errore d'accuratezza rilevato
- = contributo all'incertezza dell'errore d'accuratezza.
In questo caso l'incertezza estesa viene espressa con un fattore di copertura pari a 1 (che, in una distribuzione normale, rappresenta una probabilità pari a circa il 68 % che il valore vero del misurando ricada all'interno dell'intervallo tra il valore misurato ), anche se, normalmente, nei documenti le incertezze estese vengono espresse con fattore di copertura pari a 2, per avere una probabilità, all'interno di una distribuzione normale, del 95,45 % .
Il coefficiente di "radice 3" si applica dal momento che si considera una distribuzione rettangolare dell'incertezza. Tale scelta è dettata dal momento che è la più conservativa tra le dispersioni semplici, ossia quella che meno sottostima l'incertezza di misura.
Note[modifica | modifica wikitesto]
- ^ North Atlantic Treaty Organization, Nato Standardization Agency AAP-6 - Glossary of terms and definitions, p 43.
Voci correlate[modifica | modifica wikitesto]
- Classe di precisione
- Misurazione
- Precisione
- Sensibilità di un sistema di misura
- Standardizzazione (statistica)
Altri progetti[modifica | modifica wikitesto]
 Wikiquote contiene citazioni di o su accuratezza
Wikiquote contiene citazioni di o su accuratezza Wikizionario contiene il lemma di dizionario «accuratezza»
Wikizionario contiene il lemma di dizionario «accuratezza»
Collegamenti esterni[modifica | modifica wikitesto]
- (EN) accuracy, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.










