Notazione posizionale

Nel sistema decimale il numero 1125 è il risultato dell'operazione 5x10⁰+2x10¹+1x10²+1x10³

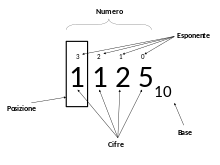
La notazione posizionale è un metodo di scrittura dei numeri, nel quale ogni posizione è collegata alla posizione vicina da un moltiplicatore, chiamato base del sistema di numerazione. Ogni posizione può essere rappresentata da un simbolo o da una quantità limitata di simboli. Il valore di una cifra equivale alla cifra stessa moltiplicata per la base elevata alla posizione di cifra precedente. Il numero di simboli necessari è almeno uguale alla base o alla più grande base ausiliaria utilizzata. Il sistema decimale consueto utilizza dieci simboli, più i simboli per i numeri segnati e i numeri con virgola, mentre il sistema sessagesimale babilonese si serve di un sistema ausiliare per ogni posizione.

Sistemi di notazione

Varie notazioni posizionali, di cui talune ibride (posizionali ed additive), permettono di rappresentare i numeri. Ecco diversi modi di scrivere il numero 9.018 in alcuni di questi sistemi.

Notazioni ibride

Le notazioni ibride utilizzano simboli che rappresentano le potenze della base, come nelle numerazioni cinese e giapponese. Così, 十 = $10$, 百 = 10², 千 = 10³, 万 = 10⁴ nel sistema giapponese. Queste numerazioni utilizzano, come per le potenze della base, simboli che rappresentano le subpotenze della base stessa. Così, 割 = 10⁻¹, 分 = 10⁻², 厘 = 10⁻³, 毛 = 10⁻⁴ nel sistema giapponese.

• Esempio

9.018 si scrive 九千十八 con il sistema utilizzato per la numerazione giapponese (decimale), ossia 9 × 1.000 + [1×]10 + 8.

Notazioni posizionali ed additive

Per la numerazione babilonese, a carattere sessagesimale, i numeri erano formati in modo additivo fino a 60, essendo i valori così ottenuti combinati secondo il principio posizionale.

• Esempio

9.018 si scrive ossia le cifre 2,30,18 (la virgola separa le cifre) che nel sistema sessagesimale babilonese significa 2×60² + 30×60¹ + 18×60⁰ = 9 018.

Notazioni esclusivamente posizionali

• Con cifre formate da una giusta posizione di elementi

9.018 si scrive

con il sistema utilizzato per la numerazione maya (vigesimale, ma irregolare), ossia 1[×7.200] + 5[×360] + 0[×20] + 18, o 1,05,00,18 con la virgola come separatore di posizioni.

• Con base ausiliaria

9.018 si scrive 2,30,38 con il sistema (sessagesimale) utilizzato per la traduzione dei testi mesopotamici, ossia 2[×3.600] + 30[×60] + 38.

• Senza base ausiliaria, senza zero

9.018 si scrive 8X18 nel sistema posizionale sperimentale senza zero (decimale), ossia 8[×1.000] + 10[×100] + 1[×10] + 8, ou 8,10,1,8, con la virgola come separatore di posizioni.

• Senza base ausiliaria, con zero

9.018 si scrive ๙๐๑๘ con il sistema utilizzato per la numerazione thai (decimale), ossia 9[×1.000] + 0[×100] + 1[×10] + 8, o 9.018, allo stesso modo dei nostri numeri arabo-indiani.

Simboli posizionali

Allo stesso modo che nel nostro sistema, nei sistemi di numerazione babilonese, maya e thai non s'impiega nessun simbolo per separare ciascuna posizione. Ciononostante, in assenza dello zero posizionale, nel sistema babilonese, poteva significare, ad esempio, tanto uno quanto sessanta. Tuttavia, in altre scritture, questi marcatori di posizione si rivelano sistematici, come la virgola utilizzata per la traduzione dei testi mesopotamici.

Solo i numeri interi avevano una rappresentazione nel sistema di numerazione maya. Nella numerazione babilonese, contrariamente alla punteggiatura che noi poniamo tra la cifra delle unità e quella dei decimi, nessun marcatore di posizione separava la parte intera dalla parte frazionaria del numero. Così, nel sistema babilonese poteva, ad esempio, non solo significare uno e sessanta, ma anche un sessantesimo. Quanto alla numerazione thai, essa utilizza, come nel nostro sistema, un marcatore di posizione per separare le potenze di mille.

Storia

Antichità

La creazione dei sistemi aritmetici posizionali, in particolare del sistema decimale, fu iniziata dai Cinesi nella loro numerazione nel II secolo a.C., poi completata verso l'anno 500 dell'era cristiana in India.

Nell'antichità, si utilizzavano esclusivamente numerosi sistemi non posizionali, il cui esempio più noto è la numerazione romana, dove, ad esempio, il numero trentotto si scrive con l'aiuto di non meno di sette cifre (XXXVIII), mentre il numero cinquanta, si accontenta di uno solo (L). È chiaro che, in un tale sistema di notazione, una semplice operazione come una moltiplicazione si rivela praticamente impossibile da effettuare senza strumenti di calcolo (abaco, tavolette di calcolo a gettoni o altri).

Medioevo

È grazie all'intemediazione di Al-Khuwarizmi (dal cui nome deriva la parola algoritmo) che gli Europei hanno preso conoscenza dell'esistenza della numerazione indiana posizionale. Verso l'anno mille, dopo aver trascorso più di cinque secoli ad interessarsi all'esistenza di questo nuovo sistema, essi lo rifiutarono ancora per quasi altri cinque secoli. E tuttavia un ecclesiastico aperto come il francese Gerbert d'Aurillac, il futuro papa di Roma Silvestro II, che per primo descrisse il sistema che utilizzavano gli Arabi di Spagna, non disse nulla in questo senso. Egli descrisse il nuovo sistema con interesse e benevolenza.

Perciò l'Europa del Medioevo continuava, forse non a torto, a fare la piccola contabilità mediante pallottolieri e gettoni, scrivendo i risultati nei testi in latino e, naturalmente, utilizzando le cifre romane non posizionali. Si può dire che il sistema aritmetico posizionale, così come i cosiddetti numeri arabi, non era utilizzato nell'Europa del Medioevo, salvo che da utilizzatori isolati e sospetti agli occhi degli altri, come ad esempio dal matematico italiano Leonardo Fibonacci e più tardi, naturalmente, il matematico francese Nicolas Chuquet.

È soltanto nel Rinascimento, con il risveglio delle scienze, che l'Europa infine comprese che non poteva più ostacolare questo nuovo sistema, mille anni (!) dopo la sua invenzione in India. Alla fine tutto il mondo occidentale ammette che quello è molto più semplice di questo. La lotta tra gli abachisti e gli algoristi, che era durata quasi tre secoli, conduce infine alla vittoria sul campo di questi ultimi.

La notazione posizionale ha reso possibile una rappresentazione semplice di tutti i numeri. Fu una delle maggiori scoperte della storia della matematica. Essa ha permesso lo sviluppo dell'aritmetica e della matematica moderna.

Voci correlate

• Sistema di numerazione
• Base (aritmetica)
• Cifra
• Binary-coded decimal

Altri progetti

Altri progetti

• Wikimedia Commons

• Wikimedia Commons contiene immagini o altri file su notazione posizionale

Collegamenti esterni

• (EN) positional numeral system, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.