Sistema di numerazione babilonese
Il sistema di numerazione babilonese è il sistema numerico utilizzato dalle società mesopotamiche, un sistema sessagesimale in cui le 60 cifre vengono scritte con un sistema additivo basato su tre simboli:
- un chiodo verticale (
 ) rappresenta l'unità;
) rappresenta l'unità; - un punzone con la punta diretta a sinistra (
 ) rappresenta la decina;
) rappresenta la decina; - due chiodi obliqui (
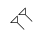 ) indicano la quantità nulla dell'entità numerica a cui fanno riferimento (così come lo zero viene usato nel sistema decimale per indicare la quantità nulla delle unità oppure delle decine e dei multipli seguenti, allo stesso modo nel sistema sessagesimale i due chiodi obliqui indicano quantità nulla delle unità oppure delle sessantine e dei multipli seguenti).
) indicano la quantità nulla dell'entità numerica a cui fanno riferimento (così come lo zero viene usato nel sistema decimale per indicare la quantità nulla delle unità oppure delle decine e dei multipli seguenti, allo stesso modo nel sistema sessagesimale i due chiodi obliqui indicano quantità nulla delle unità oppure delle sessantine e dei multipli seguenti).
Le civiltà mesopotamiche furono le prime a utilizzare sia il principio posizionale sia il numero zero.
60 numeri (lo zero e le altre 59 cifre)[modifica | modifica wikitesto]
Inizialmente, nel sistema di numerazione sessagesimale babilonese lo zero è rappresentato da un "blank space"[1], in lingua italiana "spazio bianco" oppure "spazio vuoto", mentre le restanti 59 cifre vengono scritte con caratteri speciali, detti in lingua italiana "chiodi" e "punzoni", combinati tra loro seguendo un sistema di numerazione additivo. A seconda dell'epoca e del luogo alcune cifre venivano scritte in modo un poco diverso, per esempio i numeri sette, otto e nove venivano espressi con tre file di chiodi oppure con due file soltanto, fermo restando che la quantità totale di chiodi era la stessa in entrambe le raffigurazioni. Nella tabella seguente riportiamo i segni cuneiformi numerici presenti nel Pennsylvania Sumerian Dictionary Project[2]:

Caratteristiche[modifica | modifica wikitesto]
Con il sistema di numerazione babilonese i numeri inferiori al 60 vengono scritti con un sistema di numerazione additivo, per esempio il numero 19 viene scritto sommando una decina a nove unità e si scrive quindi con un punzone e nove chiodi:
il numero 40 viene scritto sommando 4 decine:
I numeri superiori al 60 vengono scritti utilizzando un sistema posizionale le cui cifre sono quelle create con il sistema additivo, per cui se indichiamo con a il valore di una cifra nella prima posizione, il suo valore nella n-esima posizione sarà a × 60n-1. Il numero 68 viene quindi visto come 68 = 1 × 601 + 8 × 600 e viene scritto:
Il numero 132 nel sistema babilonese viene visto come 132 = 2 × 601 + 12 × 600 e viene rappresentato nel seguente modo:
Il numero 7514 = 2 × 602 + 5 × 601 + 14 × 600 viene scritto in questo modo:
Inconvenienti[modifica | modifica wikitesto]
Il sistema di numerazione babilonese presenta alcuni inconvenienti. Il fatto di utilizzare un sistema di numerazione misto tra quello additivo e quello posizionale crea delle ambiguità, per esempio i numeri 2 e 61 nel sistema babilonese vengono scritti utilizzando gli stessi simboli (![]() ) e possono essere confusi. Questo problema è stato ovviato dai babilonesi inserendo uno spazio tra le diverse posizioni. Il numero 2 può essere quindi rappresentato come
) e possono essere confusi. Questo problema è stato ovviato dai babilonesi inserendo uno spazio tra le diverse posizioni. Il numero 2 può essere quindi rappresentato come ![]() mentre il numero 61, grazie all'uso dello spazio, come
mentre il numero 61, grazie all'uso dello spazio, come ![]()
![]() .
.
Un problema ulteriore del sistema babilonese è caratterizzato dal fatto che le posizioni vuote indicanti quantità nulle non sono visivamente esplicite e quindi, per esempio, il numero ![]()
![]() non si capisce se sia un 64 = 1 × 601 + 4 × 600 oppure un 3604 = 1 × 602 + 0 × 601 + 4 × 600 oppure un 216 004 = 1 × 603 + 0 × 602 + 0 × 601 + 4 × 600. Per risolvere questo problema è stato introdotto l'uso del simbolo di due chiodi obliqui verso la fine del periodo paleobabilonese (fine del secondo millennio a.C.)[3] per indicare la quantità nulla dell'entità numerica presente in quella posizione:
non si capisce se sia un 64 = 1 × 601 + 4 × 600 oppure un 3604 = 1 × 602 + 0 × 601 + 4 × 600 oppure un 216 004 = 1 × 603 + 0 × 602 + 0 × 601 + 4 × 600. Per risolvere questo problema è stato introdotto l'uso del simbolo di due chiodi obliqui verso la fine del periodo paleobabilonese (fine del secondo millennio a.C.)[3] per indicare la quantità nulla dell'entità numerica presente in quella posizione:
Con l'uso di tale segno, il numero 3604 = 1 × 602 + 0 × 601 + 4 × 600, che necessita di una quantità nulla della quantità 601 per essere rappresentato, sarà quindi scritto come:
Il simbolo ![]() equivale alla cifra 0 del sistema di numerazione arabo nel suo indicare la quantità nulla relativa a una posizione vuota.
equivale alla cifra 0 del sistema di numerazione arabo nel suo indicare la quantità nulla relativa a una posizione vuota.
Note[modifica | modifica wikitesto]
- ^ Rudolf Hajossy, Plimpton 322 : A Universal Cuneiform Table for Old Babylonian Mathematicians, Builders, Surveyors and Teachers (PDF), in Tatra Mountains: Matehematical Publications, vol. 106, n. 67, 2016.
- ^ The Pennsylvania Sumerian Dictionary, su psd.museum.upenn.edu. URL consultato il 12 luglio 2018 (archiviato dall'url originale il 26 giugno 2013).
- ^ Jens Høyrup, A hypothetical history of Old Babylonian mathematics: places, passages, stages, development.
Voci correlate[modifica | modifica wikitesto]
Altri progetti[modifica | modifica wikitesto]
 Wikimedia Commons contiene immagini o altri file su sistema di numerazione babilonese
Wikimedia Commons contiene immagini o altri file su sistema di numerazione babilonese









