Rumore (elettronica)

In elettronica il rumore è una forma di segnale elettrico indesiderato (disturbo, interferenza, ecc), interno o esterno, che può sommarsi al segnale originario, provocando perdite e/o alterazioni dell'informazione.
Descrizione[modifica | modifica wikitesto]
Si distingue tra rumore e disturbo: per rumore solitamente si intendono segnali di origine aleatoria provenienti dall'interno e vengono descritti in termini probabilistici, mentre i disturbi sono segnali che provengono dall'esterno e possono pertanto essere descritti in termini deterministici ovvero interferenze.
Il rumore consiste di "fluttuazioni" dovute a proprietà fondamentali della materia e in quanto tali di origine interna e non eliminabili (es: rumore termico). Queste fluttuazioni che si osservano a livello macroscopico derivano da fluttuazioni a livello microscopico. Si manifestano nella forma di segnali casuali il cui andamento nel tempo non è descrivibile analiticamente, ma solo in termini statistici.
L'effetto indesiderato consiste dunque in un'alterazione o distorsione del segnale utile contenente informazione tale da poter inficiare (ad esempio) il corretto processo di rilevazione/elaborazione a valle della trasmissione.
Tipi di rumore[modifica | modifica wikitesto]
La sorgente di rumore più comune negli apparati e dispositivi elettronici è il rumore termico, esso è infatti intrinseco di ogni elemento dissipativo (es. resistori) che si trovi ad una temperatura diversa dallo zero assoluto. Poiché il rumore termico è la principale sorgente del rumore interno è solito intendere, per convenzione, come rumore interno solo quello termico.
Scoperto da Johnson e teorizzato analiticamente da Nyquist, questo rumore è conseguenza dell'agitazione termica dei portatori di carica in un conduttore. Infatti, poiché la distribuzione degli elettroni all'interno di un conduttore in funzione del tempo non è uniforme, in un certo istante si può manifestare un eccesso di cariche a una estremità, mentre nell'istante successivo questo eccesso può trasferirsi all'altra.
Il loro movimento caotico è tale da creare ai capi di un resistore una differenza di potenziale che mediamente vale 0 Volt (si dice che il valore medio del processo rumore bianco è nullo) perché il numero degli elettroni che fluiscono verso un'estremità del conduttore è uguale al numero di quelli che fluiscono verso l'altra. Tale tensione se misurata con uno strumento che non carichi il resistore è altamente variabile e descrivibile solo in termini statistici: il valore quadratico medio (quadrato del valore efficace) dipende dalla temperatura ed è pari a
dove:
- k= W/Hz*K è la costante di Boltzmann;
- R è la resistenza elettrica del conduttore;
- è la banda equivalente di rumore;
- T è la temperatura in kelvin (K)
Si può quindi affermare che un qualsiasi resistore rumoroso avente resistenza R, detto resistore caldo, può essere rappresentato con un resistore avente lo stesso valore di resistenza R di quello rumoroso, detto resistore freddo, in serie ad un generatore di tensione di rumore il cui valore efficace è dato dall'equazione sopra citata.
Altri rumori elettronici (oltre al rumore termico):
- rumore shot
- rumore 1/f (o rumore Flicker)
- rumore Burst
- rumore valanga
- rumore ottico cioè fotoni indesiderati prodotti negli apparati optoelettronici in conseguenza del fenomeno dell'emissione spontanea.
Tra i disturbi:
- Segnali armonici prodotti da rapide variazioni di corrente in sistemi oscillanti
- Disturbi elettrici di provenienza esterna (vedi compatibilità elettromagnetica)
- Il clutter (nei sistemi Radar)
Trattazione matematica[modifica | modifica wikitesto]
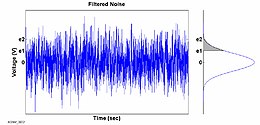
In genere il rumore, essendo intrinsecamente stocastico, viene analizzato usando la teoria dei processi stocastici: si assume perciò che il rumore sia stazionario, cioè ha proprietà invarianti nel tempo, e sia ergodico cioè tutte le proprietà d'insieme del processo sono estraibili da una singola osservazione. Perché sia possibile trattare il rumore bisogna che se ne possa associare una qualche distribuzione di probabilità. In genere se la distribuzione è gaussiana, come nella maggior parte dei casi, allora la sua distribuzione è nota:
dove rappresenta il suo valore medio e la sua deviazione standard entrambi costanti nel tempo se il processo è stazionario. Inoltre è necessario conoscere la funzione di autocorrelazione:
che rappresenta la correlazione fra due campioni del processo a distanza temporale . la correlazione è massima per , cioè quando la correlazione è il valore quadratico medio del processo.
Per , la funzione di autocorrelazione rappresenta il grado di prevedibilità di una realizzazione al tempo una volta nota al tempo t.

Dunque lo studio del rumore passa per la definizione di una appropriata distribuzione di probabilità e come funzione di correlazione nel caso dei segnali che ci interessa si usa lo spettro di potenza e si utilizzano le relazioni di Wiener-Chinčin:
cioè della trasformata e antitrasformata di Fourier della funzione di autocorrelazione. Lo spettro ottenuto è , ma in genere essendo simmetrico si utilizza lo spettro di potenza unilatero positivo. Le relazioni di Wiener-Chinčin possono allora scriversi esplicitamente:
A seconda dei casi le grandezze possono essere misurate in tensione allora l'unità di misura degli spettri è o in corrente allora . Dagli spettri di potenza dei segnali si possono anche ricavare gli spettri di ampiezza di rumore:
Per calcolare il valore efficace della tensione o della corrente in un intervallo di banda si applica semplicemente:
Voci correlate[modifica | modifica wikitesto]
- Rumore bianco
- Rumore rosa
- Rumore termico
- Rumore gaussiano
- Radiofrequenza
- Cifra di rumore
- Temperatura equivalente di rumore
- Rapporto segnale/rumore
Altri progetti[modifica | modifica wikitesto]
 Wikimedia Commons contiene immagini o altri file su rumore
Wikimedia Commons contiene immagini o altri file su rumore
Collegamenti esterni[modifica | modifica wikitesto]
- Direttiva 89/336/CEE sui disturbi di radiofrequenza (PDF), su italtec.it.
- (EN) random noise / noise, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
| Controllo di autorità | Thesaurus BNCF 30807 |
|---|












![{\displaystyle S_{xx}(\omega )=\mathbf {F} [R_{xx}(\tau )]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/753ae49f217d1fcbbe00f6451dad330dac59e5d7)
![{\displaystyle R_{xx}(\tau )=\mathbf {F} ^{-1}[S_{xx}(\omega )]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5351679e949d151b8008260c51e653bddd1bc3dd)





![{\displaystyle V_{n}(\omega )={\sqrt {S_{vv}(\omega )}}\,\,\,\,\,[V/{\sqrt {Hz}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f075f0d39c13607c729028560002e3d2da026e62)
![{\displaystyle I_{n}(\omega )={\sqrt {S_{ii}(\omega )}}\,\,\,\,\,[A/{\sqrt {Hz}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ca53f8c6e52dc294617e30abac4e18f7801e8e0)
