Inversione di popolazione
In fisica, più specificamente in meccanica statistica, si definisce inversione di popolazione la condizione per cui in un sistema costituito da componenti elementari (per esempio molecole, atomi o particelle) ci sono più elementi in stato eccitato che in quello di minore energia.
Questa particolare condizione è la chiave per ottenere l'emissione laser e per il funzionamento di alcuni tipi di transistor, diodi e altri strumenti composti da semiconduttori.
L'interazione luce-materia[modifica | modifica wikitesto]
Ci sono tre tipi possibili di interazione tra un sistema atomico e la luce:
Assorbimento[modifica | modifica wikitesto]
Se una luce di frequenza ν21 passa attraverso un gruppo di atomi che si trovano allo stato fondamentale, esiste la possibilità che la radiazione venga assorbita, causando la loro transizione a uno stato energetico eccitato. La probabilità di assorbimento è proporzionale a due fattori: l'intensità della radiazione e la popolazione N1 allo stato fondamentale. Su questo effetto è basato ad esempio un fotorivelatore o fotodiodo.
Emissione spontanea[modifica | modifica wikitesto]
Se un certo numero di atomi si trovano nello stato eccitato, può avvenire un decadimento spontaneo allo stato fondamentale con una probabilità proporzionale al loro numero N2. La differenza in energia tra i due stati ΔE viene emessa dagli atomi sotto forma di fotoni di frequenza ν21.
I fotoni sono emessi in maniera stocastica e senza relazioni di fase; in altre parole, l'emissione spontanea avviene in maniera incoerente, come in una normale lampadina. In assenza di ulteriori processi, il numero di atomi nello stato eccitato al tempo t è dato dalla relazione:, dove N2(0) è il numero di atomi eccitati al tempo t=0, e τ21 è il tempo di vita medio della transione tra i due stati.
Emissione stimolata[modifica | modifica wikitesto]
Se un atomo si trova già nello stato eccitato, potrebbe essere perturbato dal passaggio di un fotone dotato di una frequenza ν21 corrispondente al gap energetico di transizione tra lo stato eccitato e lo stato fondamentale. In questo caso l'atomo eccitato collassa allo stato fondamentale inducendo la produzione di un secondo fotone di frequenza ν21. Il fotone originale non è assorbito dall'atomo, e così il risultato complessivo sono due fotoni di medesima frequenza. Questo processo è noto come emissione stimolata, e la sua rate è proporzionale al numero di atomi N2 nello stato eccitato e dalla densità di radiazione della luce
Il dettaglio fondamentale dell'emissione stimolata è che il fotone indotto ha la medesima frequenza e costante di fase dell'inducente: i due si trovano così ad essere coerenti. Questa proprietà permette l'amplificazione ottica, e la produzione del sistema laser. Durante l'intera fase di laseraggio tutti e tre i tipi di interazione luce-materia sopra descritti avvengono. Inizialmente gli atomi vengono portati allo stato eccitato mediante un processo detto di pompaggio che descriveremo poi. Alcuni di questi atomi decadranno per emissione spontanea, rilasciando luce incoerente sotto forma di fotoni di frequenza ν. Alcuni di questi fotoni verranno assorbiti dagli atomi dello stato fondamentale e andranno persi nel fenomeno del laseraggio. Altri fotoni andranno a causare emissione stimolata negli atomi eccitati, che reagiranno rilasciando un ulteriore fotone coerente dando origine all'amplificazione ottica.
Se il numero di fotoni che sono amplificati per unità di tempo è maggiore rispetto a quelli assorbiti ciò che si ottiene è un continuo incremento di quelli prodotti: il laser viene dichiarato oltre la soglia.
Nella descrizione precedentemente fatta dei fenomeni di assorbimento ed emissione abbiamo detto che la probabilità di questi due processi sono entrambi proporzionali al numero di atomi sullo stato fondamentale N1 e su quello eccitato N2. Se lo stato fondamentale ha una popolazione più elevata rispetto a quella di quello eccitato (N1 > N2), il processo di assorbimento dominerà e ci sarà una attenuazione nel numero di fotoni. Se la popolazione dei due stati sarà la medesima (N1 = N2), la probabilità di assorbimento della luce bilancerà esattamente la probabilità di emissione; il materiale matrice del laser diviene otticamente trasparente
Se invece il livello ad energia più elevata ha una popolazione maggiore rispetto a quello ad energia più bassa ((N1 < N2), il processo di emissione dominerà, e la luce nel sistema andrà aumentando. È chiaro quindi che per produrre una maggiore probabilità di emissione stimolata piuttosto che di assorbimento è richiesto che il rapporto di popolazione tra i due stati sia N2/N1 > 1, ossia per il fenomeno laser è richiesta una inversione di popolazione.
La popolazione e la distribuzione di Boltzmann[modifica | modifica wikitesto]
Per capire cos'è una inversione di popolazione è necessario prima studiare come è costituita una "popolazione normale" nella meccanica statistica. Prendiamo ad esempio un gruppo di atomi, supponendo per semplicità che possano assumere solo due stati energetici diversi, il primo con energia E1 e l'altro con energia E2. Diciamo che E2>E1, per cui lo stato 1 sarà lo stato fondamentale e il 2 lo stato eccitato.
Ogni atomo nello stato eccitato ha una certa probabilità P21 di decadere nello stato fondamentale emettendo energia, entro un certo intervallo di tempo, e ogni atomo nello stato fondamentale ha una certa probabilità P12 di assorbire energia (dagli altri atomi del sistema, o da urti con l'esterno del sistema stesso) e di passare nello stato eccitato, nello stesso intervallo di tempo. Quindi, il rapporto fra atomi eccitati e atomi normali dipenderà sia dal rapporto fra le due distribuzioni stocastiche (che descrivono il numero di atomi nello stato relativo al passare del tempo) sia dalla temperatura del sistema, che esprime la densità di energia mediamente disponibile nel sistema; poiché le due distribuzioni sono esponenziali, la formula risultante è:
dove e sono rispettivamente il numero di atomi nel secondo e nel primo stato, T è la temperatura del sistema e k è la costante di Boltzmann. T deve essere espressa in kelvin o in gradi Rankine. Le due probabilità P12 e P21 sono identiche (la dimostrazione di questo fatto fu uno dei risultati più importanti di tutta la fisica del XIX secolo) e sono "incorporate" nella costante di Boltzmann.
Considerando degli atomi a temperatura ambiente all'equilibrio termodinamico, con un salto di energia fra i due stati di 2,07 eV (un valore pari all'energia media di un fotone di luce visibile) la frazione di atomi in stati eccitati è infinitesimo: 1,8 x 10-38. Esso cresce lentamente all'aumentare della temperatura, ma rimane sempre molto piccolo; a una temperatura di 4000 K avremmo ancora solo quattro atomi eccitati su diecimila. Ottenere una inversione di popolazione a temperatura ambiente è impossibile, se non si altera l'equilibrio termodinamico del sistema con una fonte di energia esterna.
Creare una inversione di popolazione[modifica | modifica wikitesto]
È ugualmente impossibile raggiungere una condizione di inversione di popolazione in un sistema di atomi che abbiano soltanto due stati energetici possibili: poiché la probabilità di salto energetico da uno stato all'altro è la stessa nei due sensi, il massimo che potremmo ottenere sarebbe un "pareggio": lo stesso numero di atomi in tutti e due gli stati. Per ottenere il risultato che cerchiamo ci servono degli atomi che possano assumere (almeno) tre stati energetici diversi. Nel caso dei laser, i dispositivi che più di tutti sfruttano il fenomeno dell'inversione di popolazione, si usano (quasi) solo sistemi atomici a tre o a quattro livelli energetici; nei dispositivi a semiconduttore non esistono livelli energetici ma intere bande di energie permesse; in questo caso il fenomeno dell'inversione di popolazione si esprime nello svuotamento e nel riempimento di queste bande da parte degli elettroni e delle lacune.
Sistemi a tre livelli di energia[modifica | modifica wikitesto]
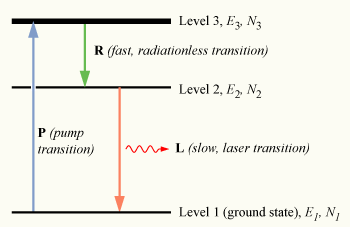
Per raggiungere la condizione di non equilibrio, è necessario ricorrere a un metodo indiretto per popolare lo stato eccitato. Per comprendere come esso viene realizzato, possiamo utilizzare come modello il cosiddetto sistema "laser a tre livelli". Consideriamo di nuovo un sistema di N atomi, in questo caso con ogni atomo capace di esistere in uno qualsiasi dei tre livelli di energia, con livelli numerati 1,2, e 3, con energie E1,E2 e E3, e popolazioni N1, N2 e N3, rispettivamente.
Da notare che E1 < E2 < E3; con l'energia del livello 2 intermedia tra lo stato fondamentale e quella dello stato 3.
Inizialmente il sistema di atomi si trova all'equilibrio termico e la maggior parte degli atomi si troverà sullo stato fondamentale: N1 ≈ N, N2 ≈ N3 ≈ 0. Se noi ora sottoponiamo gli atomi per esempio a una radiazione luminosa di frequenza ν31, dove E3-E1 = hν31, il processo di assorbimento ottico ecciterà gli atomi dallo stato fondamentale al livello 3. Questo processo è chiamato pompaggio, e in generale non coinvolge sempre direttamente l'assorbimento luminoso; altri metodi per eccitare il materiale matrice del laser utilizzano scariche elettriche oppure reazioni chimiche. Il livello 3 viene chiamato livello di pompaggio, e la transizione energetica E1 → E3 transizione di pompaggio, che viene indicata con P nell'immagine.
Se noi continuiamo a pompare gli atomi, ecciteremo un gran numero di questi nel livello 3, così che N3 > 0. In un materiale medium per laser è richiesto che questi atomi eccitati transiscano rapidamente al livello 2. L'energia rilasciata in questa transizione potrebbe essere emessa sotto forma di fotone (emissione spontanea) ma in pratica la transizione 3→2 (indicata con R nel diagramma) è usualmente non radiativa, con l'energia trasferita sotto forma di moto vibrazionale al materiale circostante l'atomo, senza la generazione effettiva di un fotone.
A questo punto un atomo che si trova sul livello 2 può decadere con emissione spontanea allo stato fondamentale, rilasciando un fotone di frequenza ν21 (dato da E2-E1 = hν21), decadimento indicato con la lettera L nel diagramma, che prende il nome di transizione laser . Se la vita media di questa transizione, τ21 è maggiore del tempo di vita medio della transizione non radiativa 3→2 τ32 (se τ21 >> τ32), la popolazione dell'E3 sarà fondamentalmente 0 (N3 ≈ 0) e la popolazione dello stato eccitato sarà accumulata nel livello 2 (N2 > 0). Se più della metà degli N atomi può essere accumulata in questo stato, questo diventerà maggiore rispetto a quella dello stato fondamentale N1. Una inversione di popolazione (N2 > N1 ) è così stata ottenuta tra i livelli 1 e 2, e l'amplificazione ottica alla frequenza ν21 può iniziare.
Poiché almeno metà della popolazione di atomi deve essere eccitata dallo stato fondamentale per ottenere l'inversione di popolazione, il medium del laser deve subire un pompaggio molto elevato. Ciò rende il sistema laser a tre livelli sostanzialmente inefficiente, nonostante sia stato il primo tipo di laser a essere sviluppato, utilizzando come materiale matrice il rubino nel 1960 da Theodore Maiman. Un sistema laser a tre livelli può presentare anche, come ulteriore inconveniente, una transizione radiativa tra i livelli 3 e 2, e una non radiativa tra il 2 e l'1.
Sistemi a quattro livelli di energia[modifica | modifica wikitesto]

In questo caso ci troviamo a lavorare con quattro livelli di energia, di energia E1, E2, E3, E4, e popolazione N1, N2, N3, N4, rispettivamente. Le energie di ciascun livello sono prese così che E1 < E2 < E3 < E4. In questo sistema, la transizione di pompaggio P eccita gli atomi dello stato fondamentale (livello 1) entro la banda di pompaggio (livello 4). Da quest'ultimo livello, avviene un rapido decadimento non radiativo Ra al livello 3. Poiché il tempo di vita medio della transizione laser L è lungo rispetto a quello Ra (τ32 >> τ43), la popolazione va aumentando sul livello 3 (che prende il nome di livello laser superiore), il quale a questo punto può rilassare spontaneamente oppure per emissione stimolata al livello 2 (livello laser inferiore). Questo livello ha poi un rapido decadimento non radiativo Rb allo stato fondamentale.
Come prima, la presenza di una transizione di decadimento non radiativa comporta che la popolazione della banda di pompaggio si svuoti rapidamenete (N4 ≈ 0). Lo stesso avviene nel livello laser inferiore con energia E2 dove gli atomi rilassano rapidamente sullo stato fondamentale, quindi (N2 ≈ 0). Questa ultima considerazione è particolarmente importante, poiché qualunque accumulo di popolazione sul livello 3 comporterà una situazione di inversione di popolazione rispetto al livello 2. Infatti, N3 > 0 implica che N3 > N2. Perciò l'amplificazione ottica e il laseraggio avverranno a una frequenza di ν32 (E3-E2 = hν32).
Poiché è necessario che solo pochi atomi vengano eccitati nel livello laser superiore per arrivare in condizioni di inversione di popolazione, un sistema laser a quattro livelli si rivela molto più efficiente di un sistema a tre livelli. In termini reali, in un processo laser sono coinvolti più di quattro livelli energetici, con fenomeni di eccitazione e rilassamento più complessi tra questi livelli. In particolare la banda di pompaggio può essere costituita da più livelli energetici distinti, il che consente il pompaggio ottico del medium mediante un gran numero di lunghezze d'onda.
Da notare che sia nei sistemi a tre livelli che in quelli a quattro, l'energia della transizione di pompaggio è maggiore rispetto a quella della transizione laser. Questo comporta che, se un laser è pompato otticamente, la frequenza della luce pompante deve essere maggiore di quella risultante dalla luce laser. In altre parole, la lunghezza d'onda del pompaggio è più piccola della lunghezza d'onda del laser. È possibile però in alcuni medium usare l'assorbimento multiplo di fotoni tra differenti transizioni a bassa energia per arrivare al livello di pompaggio: i laser che utilizzano questo tipo di soluzione prendono il nome di laser ad alta conversione.
In molti laser, come descritto nei modelli sopra presentati, il laseraggio coinvolge la transizione di atomi tra differenti stati energetici elettronici, ma va considerato che questo non è il solo meccanismo che può portare al fenomeno del laser. Per esempio, ci sono molti tipi di laser comuni (per esempio quelli a diossido di carbonio) dove il medium laser è costituito da molecole complete, e i livelli energetici corrispondono ai modi rotazionali e vibrazionali delle molecole.
Bibliografia[modifica | modifica wikitesto]
- Svelto, Orazio (1998). Principles of Lasers, 4th ed. (trans. David Hanna), Springer. ISBN 0-306-45748-2
- Demtröder, W., Atoms, Molecules and Photons. Springer-Verlag (2006)
Voci correlate[modifica | modifica wikitesto]
Collegamenti esterni[modifica | modifica wikitesto]
- (EN) population inversion, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
| Controllo di autorità | GND (DE) 4434069-2 |
|---|



