Assonometria

L'assonometria (o 'proiezione assonometrica, dal greco áxon, asse e métron, misura, cioè misura in base agli assi) è un metodo di rappresentazione grafica trattato dalla geometria descrittiva. Fu formalizzata dall'inglese William Farish nella prima metà dell'Ottocento. Rappresentazioni assonometriche erano già utilizzate nel tardo medioevo per la realizzazione di fortezze militari ma venivano derivate dalla prospettiva tanto da essere chiamate prospettive militari[1]
L'assonometria si basa sull'utilizzo di tre assi geometrici (semirette) che hanno un unico punto di origine O e sui quali sono riportate le tre dimensioni che un oggetto possiede nello spazio reale.
Il principio alla base dell'assonometria è la proiezione di un oggetto geometrico su un piano (piano di proiezione o quadro), lungo la direzione determinata da un punto improprio (retta di proiezione o centro di proiezione), cioè posto all'infinito. Una caratteristica dell'assonometria è di poter rappresentare contemporaneamente tutte le dimensioni di un oggetto.
Differisce dalla prospettiva poiché non rappresenta ciò che l'occhio effettivamente vede: in particolare le linee parallele rimangono parallele e gli oggetti distanti non si riducono di dimensioni. Può essere considerata una prospettiva conica il cui centro è stato posto all'infinito, cioè molto lontano dall'oggetto osservato.
Le proiezioni assonometriche si basano sul Teorema di Polke, secondo il quale ogni tripla di vettori complanari può essere sempre ottenuta come una proiezione di una tripla di vettori ortogonali tra loro, posti nello spazio euclideo.
Un'assonometria viene detta ortogonale oppure obliqua a seconda che il raggio di proiezione sia o meno ortogonale al piano di proiezione. Inoltre una assonometria può essere classificata anche in base alle riduzioni assonometriche applicate (ovvero la modifica delle misure dei tre assi del sistema di riferimento). Per questo un'assonometria, tanto ortogonale che obliqua, può essere monometrica se la costante di riduzione è uguale su tutti gli assi; dimetrica, se la costante di riduzione è uguale solo su due assi; oppure trimetrica, se la costante di riduzione è diversa per tutti gli assi.
Assonometria obliqua
[modifica | modifica wikitesto]Si ha l'assonometria obliqua quando il raggio di proiezione è obliquo rispetto al quadro di proiezione. In considerazione del fatto che il quadro può essere parallelo ad un piano del triedro di riferimento (xyz), o incidente a tutte le sue facce, l'assonometria può essere rispettivamente di due tipi: l'assonometria cavaliera e l'assonometria generica.
Assonometria cavaliera
[modifica | modifica wikitesto]L'assonometria cavaliera[2] è un tipo di assonometria obliqua in cui il piano di proiezione (detto anche quadro) è parallelo a uno dei tre piani del sistema di riferimento.[3] Un'assonometria cavaliera può essere solo monometrica (tutte le misure sugli assi rimangono invariate) oppure dimetrica (si riduce la misura dell'asse perpendicolare al quadro).
Assonometria cavaliera frontale
[modifica | modifica wikitesto]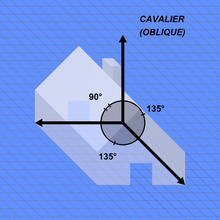
L'assonometria cavaliera viene detta frontale se il piano di proiezione è verticale (xz o yz).
Siccome il quadro è parallelo al piano verticale, il prospetto frontale mantiene la vera forma e misure.
Per convenzione nella "cavaliera rapida" l'asse perpendicolare al quadro (asse y) viene inclinato 45° rispetto all'asse orizzontale. Inoltre, per non renderla innaturale all'occhio umano, si compie una riduzione assonometrica dimezzando le misure relative all'asse y.
L'assonometria cavaliera rapida viene utilizzata di frequente a motivo della sua facilità di costruzione, ma è possibile rappresentare l'asse y inclinato e con misure a piacere, purché proporzionali.
-
Cerchio in assonometria cavaliera frontale
Assonometria cavaliera militare
[modifica | modifica wikitesto]
L'assonometria cavaliera viene detta militare se il piano di proiezione è orizzontale.
Siccome il quadro è parallelo al piano orizzontale, la pianta mantiene la vera forma e misure. Per questo motivo era usata nel passato da ingegneri militari per rappresentare rapidamente l'estensione di fortificazioni.
Per rendere l'assonometria più compatta, si può compiere una riduzione assonometrica dimezzando le misure relative alle altezze (asse z).
L'assonometria cavaliera militare che non ha subito riduzioni sull'asse z è detta semplicemente assonometria monometrica.
Assonometria generica
[modifica | modifica wikitesto]I raggi di proiezione sono obliqui rispetto al quadro e a sua volta il quadro è inclinato rispetto al triedro di riferimento (xyz). Dunque gli assi della terna di riferimento xyz formano angoli diversi con il quadro. Si differenzia dall'assonometria trimetrica ortogonale (vedi sotto) per il fatto che l'immagine O' dell'origine O degli assi xyz non coincide con l'ortocentro del triangolo delle tracce txy, txz, tyz.
Assonometria ortogonale
[modifica | modifica wikitesto]Si ha l'assonometria ortogonale quando i raggi proiettanti sono ortogonali al quadro di proiezione, il quale tuttavia deve essere inclinato rispetto ai tre piani di riferimento. A seconda degli angoli che forma il quadro con gli assi di riferimento xyz, l'assonometria ortogonale può essere isometrica, dimetrica o trimetrica.[4]
Assonometria isometrica
[modifica | modifica wikitesto]
Un'assonometria ortogonale è detta isometrica quando gli assi formano tra loro tre angoli uguali. In questo caso il quadro di proiezione è inclinato in egual misura rispetto a tutti e tre i piani principali e quindi il triangolo delle tracce è un triangolo equilatero. Siccome gli assi formano tre angoli uguali, i rapporti di riduzione lungo i tre assi sono uguali tra loro. Molto spesso, per comodità, vengono riportate direttamente le misure reali causando un leggero ingrandimento della proiezione.
Per una corretta esecuzione, preso come riferimento l'asse verticale z, bisogna tracciare un asse y inclinato di 120° rispetto all'asse verticale che guardi verso destra e un asse x inclinato di 120° rispetto all'asse verticale che guardi verso sinistra.
-
Cerchio in assonometria isometrica
-
Una rappresentazione in assonometria isometrica
Assonometria dimetrica
[modifica | modifica wikitesto]Un'assonometria ortogonale è detta dimetrica quando gli assi formano tra loro due angoli uguali ed uno diverso. In questo caso il quadro di proiezione è inclinato in egual misura rispetto a due piani ma non al terzo e quindi il triangolo delle tracce è un triangolo isoscele. Siccome due dei tre assi formano lo stesso angolo con il piano di proiezione, i rapporti di riduzione saranno medesimi sui due assi e diversi sull'altro.
Assonometria trimetrica
[modifica | modifica wikitesto]Un'assonometria ortogonale viene detta trimetrica quando gli assi formano tra loro tre angoli diversi. In questo caso il quadro di proiezione è diversamente inclinato rispetto tutti e tre i piani e quindi il triangolo delle tracce è un triangolo scaleno. Siccome gli assi formano tra loro tre angoli diversi i rapporti di riduzione saranno diversi su tutti e tre gli assi.
Note
[modifica | modifica wikitesto]- ^ Cfr. Massimo Scolari, Elementi per una storia dellaxonometria.
- ^ Il termine francese cavalier indicava una collina artificiale posta all'interno di una fortificazione militare che permetteva di vedere al di là delle mura la zona sottostante. Cfr Etymologie des maths
- ^ Le proiezioni assonometriche (PDF), su architettura-old.unicampania.it. URL consultato il 12 settembre 2021 (archiviato dall'url originale il 12 settembre 2021).
- ^ C. Bonfigli e C. R. Braggio, Geometria descrittiva e prospettiva, Hoepli, 2000.
Voci correlate
[modifica | modifica wikitesto]- Proiezioni ortogonali
- Planivolumetria
- Proiezione (geometria)
- Spaccato
- Teorema di Pohlke
- Triangolo delle tracce
Altri progetti
[modifica | modifica wikitesto] Wikizionario contiene il lemma di dizionario «assonometria»
Wikizionario contiene il lemma di dizionario «assonometria»




