Teoria delle code
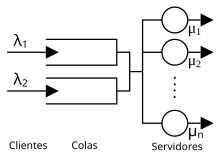
La teoria delle code è lo studio matematico delle linee di attesa (o code) e di processi correlati, quali il processo di arrivo in coda, l'attesa (essenzialmente un processo di immagazzinamento) e il processo di servizio. Può essere applicata ad un'ampia varietà di problemi, soprattutto nel campo dei trasporti, delle telecomunicazioni, della fornitura di servizi (ad es. in sanità) e delle operazioni aziendali. Usualmente considerata una branca della ricerca operativa, le sue origini risalgono al 1909 quando l'ingegnere danese Agner Krarup Erlang pubblicò un articolo intitolato The theory of probability and telephone conversations relativo alle attese nelle chiamate telefoniche.
Descrizione[modifica | modifica wikitesto]
Notazione di Kendall[modifica | modifica wikitesto]



Nel 1953, David George Kendall introdusse la notazione A/B/C, successivamente estesa come 1/2/3/4/5/6 al fine di fornire una descrizione immediata del modello del sistema a code:
- Un codice che descrive la distribuzione di probabilità dei tempi di arrivo dei jobs nel sistema; i codici più usati sono:
- "M" per "di Markov", implicante una distribuzione esponenziale negativa unilatera per i tempi di servizio o tra gli arrivi: ciò implica l'assenza di memoria di questi ultimi;
- "D" per distribuzione "degenere" o "deterministica" dei tempi di servizio;
- "E" per una distribuzione di Erlang con come parametro di forma;
- "G" per una distribuzione "generale".
- Un codice che rappresenta la distribuzione di probabilità dei tempi di servizio dei jobs, usando gli stessi simboli precedenti.
- Il numero di canali di servizio, detti anche serventi, o server (ad esempio gli sportelli alla posta).
- Le dimensioni massime del sistema, che corrisponde alla somma tra i jobs in coda e i jobs nei canali di servizio; quando il massimo viene raggiunto ulteriori arrivi vengono rifiutati. Se non indicata la dimensione si intende infinita.
- Le dimensioni della popolazione da cui possono arrivare i clienti; questo limita il ritmo di arrivi, tanti più jobs sono presenti nella coda tanti meno ne sono disponibili per entrare nel sistema. Se non indicata la dimensione si intende infinita.
- L'ordine con il quale sono serviti i jobs nella coda (per default è FIFO):
- First Come First Served (FCFS) (o First In First Out - FIFO) (il primo che arriva viene servito per primo);
- Last Come First Served (LCFS) (o Last In First Out - LIFO) (l'ultimo che arriva viene servito per primo);
- Service In Random Order (SIRO) (servizio in ordine casuale);
- PRI (esiste un sistema di selezione degli utenti a priorità (un esempio è il pronto soccorso, con i codici bianco, verde e rosso).
I modelli più studiati sono i sistemi M/M//, con e che possono assumere diversi valori (il modello più semplice è l'M/M/1, con un servente e a capacità illimitata): questo perché la distribuzione esponenziale degli intertempi di arrivo e di servizio permette di studiare i sistemi a coda come dei processi di nascita e morte.
Sistemi a coda e teoria del traffico[modifica | modifica wikitesto]


I sistemi a coda sono modellizzabili tramite catene di Markov a tempo continuo ossia con sistemi dinamici caratterizzati da stati, probabilità di stato e probabilità di transizione da uno stato a un altro uguale al prodotto tra la frequenza di transizione e l'intervallo di tempo dipendente solo dallo stato presente del sistema e non da quelli precedenti (sistema senza memoria). Lo stato rappresenta la situazione in cui si trova il sistema rispetto a variabili prese come riferimento (in linea di massima non univoche) e l'evoluzione del sistema è mappata con una sequenza di salti fra gli stati stessi. Note le frequenze di transizione, ossia la probabilità di transizione di stato, è possibile derivare le probabilità di stato risolvendo la catena di Markov; dalla conoscenza di queste probabilità si possono poi derivare i parametri prestazionali di interesse quali il traffico smaltito, la probabilità di rifiuto, il tempo di coda, ecc…
Definendo il flusso proveniente dallo stato -esimo verso lo stato -esimo come il prodotto tra la probabilità di stato in e la frequenza di transizione verso lo stato per il calcolo della probabilità di stato si utilizza la condizione espressa dalla legge di conservazione dei flussi la quale afferma che la somma dei flussi entranti è uguale alla somma dei flussi uscenti da uno stato. Applicando tale principio ad ogni stato si ottiene un sistema di equazioni in incognite (le probabilità di stato) tante quante gli stati le equazioni non sono tutte indipendenti tra loro, quindi la soluzione del sistema è impossibile (determinante nullo) a meno di sostituire un'equazione con la somma delle probabilità degli stati pari ad uno.
Un tipo di catene di Markov sono le catene di nascita e morte dove sono ammesse transizioni solo tra strati "adiacenti" e per i quali è identificabile una linea di taglio di flusso. Un sistema a coda è detto Markoviano se è modellabile tramite una catena di Markov di nascita e morte con processo di arrivo e di servizio di tipo esponenziale negativo di parametri λ (nascita) e υ (morte) e valori attesi corrispondentemente pari a 1/λ e 1/υ.
In un sistema con serventi diventa fondamentale un parametro prestazionale detto probabilità di blocco, che dipende dal numero di serventi e dal traffico offerto in ingresso. Tale parametro si calcola facendo riferimento alla formula di Erlang B i cui valori, per e fissati, sono espressi in forma tabulata. Altrettanto di interesse è la probabilità di attesa in coda espressa in funzione del numero di serventi e del traffico offerto attraverso la formula di Erlang C. In una rete di telecomunicazione i sistemi a coda e i relativi problemi di gestione del traffico sono presenti all'interno dello stack protocollare dei sistemi di elaborazione, trasmissione e ricezione del flusso informativo ossia i terminali host e i sottosistemi interni di commutazione (router) e più in generale in tutti gli apparati di rete che presentano del traffico in ingresso.
Voci correlate[modifica | modifica wikitesto]
Altri progetti[modifica | modifica wikitesto]
 Wikimedia Commons contiene immagini o altri file sulla teoria delle code
Wikimedia Commons contiene immagini o altri file sulla teoria delle code
Collegamenti esterni[modifica | modifica wikitesto]
- code, teoria delle, in Enciclopedia della Matematica, Istituto dell'Enciclopedia Italiana, 2013.
- (EN) queuing theory, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
- (EN) Eric W. Weisstein, Queuing Theory, su MathWorld, Wolfram Research.
- http://web2.uwindsor.ca/math/hlynka/queue.html
- Java Modelling Tools - Una suite GPL per la risoluzione di modelli a reti di code e per studi di performance, su jmt.sourceforge.net.
| Controllo di autorità | Thesaurus BNCF 22124 · LCCN (EN) sh85109832 · GND (DE) 4255044-0 · BNF (FR) cb12647707b (data) · J9U (EN, HE) 987007553435905171 · NDL (EN, JA) 00567524 |
|---|













