Cifrario di Cesare

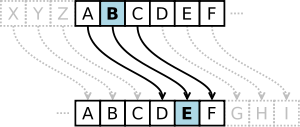
Da Wikipedia, l'enciclopedia libera.

Il cifrario di Cesare è uno dei più antichi algoritmi crittografici di cui si abbia traccia storica. È un cifrario a sostituzione monoalfabetica in cui ogni lettera del testo in chiaro è sostituita nel testo cifrato dalla lettera che si trova un certo numero di posizioni dopo nell'alfabeto. Questi tipi di cifrari sono detti anche cifrari a sostituzione o cifrari a scorrimento a causa del loro modo di operare: la sostituzione avviene lettera per lettera, scorrendo il testo dall'inizio alla fine.

In particolare, Cesare utilizzava uno spostamento di 3 posizioni (la chiave era dunque 3), secondo il seguente schema:

Testo in chiaro	a	b	c	d	e	f	g	h	i	l	m	n	o	p	q	r	s	t	u	v	z
Testo cifrato	D	E	F	G	H	I	L	M	N	O	P	Q	R	S	T	U	V	Z	A	B	C

Per cifrare un messaggio, basta prendere ogni lettera del testo in chiaro e sostituirla con la corrispondente lettera della riga testo cifrato. Per decifrare, viceversa. Ecco un semplice esempio:

Testo in chiaro	`attaccare gli irriducibili galli alla ora sesta`
Testo crittato	`DZZDFFDUH LON NUUNGAFNENON LDOON DOOD RUD VHVZD`

Cifrare (e decifrare) il testo più volte non migliora la sicurezza, in quanto una rotazione di A posti seguita da una di B posti equivale ad una di A + B. Matematicamente parlando, la cifratura con le varie chiavi forma un gruppo.

[modifica] Storia

Il cifrario di Cesare prende il nome da Giulio Cesare, che lo utilizzava per proteggere i suoi messaggi segreti. Grazie allo storico Svetonio^[1] sappiamo che Cesare utilizzava in genere una chiave di 3 per il cifrario, come nel caso della corrispondenza militare inviata alle truppe comandate da Cicerone. Al tempo era sicuro perché gli avversari spesso non erano neanche in grado di leggere un testo in chiaro, men che mai uno cifrato; inoltre non esistevano metodi di crittanalisi in grado di rompere tale codice, per quanto banale

Conosciamo anche altri che usarono questo cifrario al tempo di Cesare: Augusto, suo nipote, lo utilizzava con chiave 1 ma senza ripartire da sinistra in caso di fine dell'alfabeto. Quindi, scriveva B per A, C per B ma AA per X.

Dalla scoperta dell'analisi delle frequenze da parte del matematico arabo Al-Kindi nell'XI secolo circa, tutti i cifrari di questo tipo sono divenuti molto semplici da rompere; nessuno è adatto per comunicazioni sicure allo stato tecnologico attuale, né lo è stato negli ultimi 1000 anni.

[modifica] I "pizzini" di Provenzano

Un rudimentale sistema di cifratura basato sul cifrario di Cesare è stato usato anche da Bernardo Provenzano per proteggere informazioni rilevanti scritte nei suoi famosi pizzini, i piccoli foglietti di carta con i quali il boss della mafia, durante la sua latitanza, riceveva informazioni e impartiva ordini^[2]. Il sistema scelto da Provenzano era abbastanza semplice: si trattava di sostituire ad ogni lettera il numero corrispondente alla posizione nell'alfabeto sommato a 3 e di comporre così un singolo, lungo numero. Ad esempio, i numeri "512151522 191212154" nascondono il nome di "Binnu Riina": infatti, 5 = 2 (posizione della B) più 3; 12 = 9 (posizione della I) più 3; ecc...

[modifica] Rompere la cifratura

Con un diagramma delle frequenze delle lettere nel testo in cifra e nella lingua originale del testo, è facile individuare il valore della chiave osservandone la disposizione. Ad esempio, nella lingua italiana, le lettere più frequenti sono le vocali E, A, O ed I, con lievi differenze, seguite dalle consonanti L, N, R, S e T, mentre sono rare B, F, Q e Z e praticamente assenti le lettere straniere J, K, Y, X e W; nella lingua inglese, invece, le lettere più frequenti sono E e T, mentre le più rare sono Q e Z. Anche i computer sono in grado di eseguire simili calcoli senza difficoltà.

Il cifrario di Cesare è molto più debole di uno in cui la corrispondenza delle lettere sia casuale, come succede in molti giochi enigmistici. I luoghi più comuni dove si può trovare questo cifrario è in giochi per bambini oppure nell'algoritmo ROT13, che è fatto apposta per essere facile da decifrare.