Ellisse

Tipi di sezioni coniche:
1. Parabola
2. Circonferenza ed ellisse
3. Iperbole

In geometria, un'ellisse (dal greco ἔλλειψις elleipsis, mancanza, perché l'ellisse è un circolo imperfetto) è una curva piana ottenuta intersecando un cono con un piano in modo da produrre una curva chiusa. Affinché la sezione conica produca una curva chiusa, l'inclinazione del piano deve essere superiore a quella della generatrice del cono rispetto al suo asse. Per contro, le due sezioni coniche ottenute con piani aventi inclinazione pari o inferiore a quella della retta generatrice rispetto all'asse del cono danno vita ad altri due tipi di curve che sono però aperte e illimitate: la parabola e l’iperbole.

La circonferenza è un caso speciale di ellisse che si ottiene quando l’intersezione viene fatta con un piano ortogonale all’asse del cono.

Un’ellisse è anche il luogo dei punti di un piano per i quali la somma delle distanze da due punti fissi detti fuochi rimane costante.

L’ellisse può aversi anche dalla proiezione verticale su un piano orizzontale di una circonferenza appartenente ad un piano inclinato: se il piano inclinato forma un angolo φ con il piano orizzontale, la proiezione verticale della circonferenza è un'ellisse di eccentricità sin φ.

Si tratta infine della più semplice tra le figure di Lissajous, ottenuta dalla composizione dei due moti verticale e orizzontale di tipo sinusoidale della stessa frequenza.

In base alle leggi di Keplero, l'orbita di un pianeta è un'ellisse con il Sole che ne occupa uno dei due fuochi.

Ellisse: a è pari al semiasse maggiore, b al semiasse minore, F₁ ed F₂ sono i due fuochi, c è pari alla distanza di uno qualunque dei fuochi dal centro e infine la somma $\scriptstyle \bold {\overline{F_1X}+\overline{XF_2}}$ è costante e si dimostra essere pari a 2a, lunghezza dell'asse maggiore.

Dimostrazione geometrica dell'uguaglianza tra la somma delle distanze di un punto dell'ellisse dai due fuochi e la costante 2a (lunghezza dell'asse maggiore): se si considera in particolare il punto B dell'ellisse si nota come la somma $\scriptstyle \bold{\overline{F_1B}+\overline{F_2B}}$ sia pari alla lunghezza 2a dell'asse maggiore.

Elementi di una ellisse

L'ellisse è una curva simile a un cerchio allungato in una direzione: è un esempio di sezione conica e può essere definita come il luogo dei punti per i quali la somma delle distanze da due punti fissi, detti fuochi, rimane costante. Se i due fuochi coincidono si ha una circonferenza, che può quindi considerarsi un caso particolare di ellisse (ad eccentricità nulla).

È una curva simmetrica sia rispetto all'asse delle ascisse sia rispetto all'asse delle ordinate e sia rispetto al centro. La distanza tra i punti antipodali dell'ellisse, vale a dire tra punti simmetrici rispetto al suo centro, è massima lungo l'asse maggiore (che contiene anche i due fuochi) ed è minima lungo l'asse minore perpendicolare a quello maggiore. Il semiasse maggiore è una delle due metà dell'asse maggiore: parte dal centro, passa attraverso un fuoco e arriva all'ellisse. Analogamente il semiasse minore è metà dell'asse minore. I due assi sono per l'ellisse l'equivalente del diametro per la circonferenza, mentre i due semiassi sono l'equivalente del raggio.

La dimensione e la forma di un'ellisse sono determinate da due costanti, dette convenzionalmente a e b. La costante a è la lunghezza del semiasse maggiore mentre la costante b quella del semiasse minore.

Equazioni

Relazione tra i parametri a, b e c di un'ellisse. Se scegliamo in particolare il punto C, dovendo essere costante e pari a 2a la somma delle distanze dei due fuochi da C ed essendoci simmetria rispetto al punto C, ciascuna delle due distanze sarà pari ad a. Applicando il teorema di Pitagora si ricava che $\scriptstyle \bold{a^2 = b^2 + c^2}$

L'equazione dell'ellisse si trova eguagliando la somma delle distanze fra i due fuochi F₁(x₁;y₁) ed F₂(x₂;y₂) e un punto generico P(x;y) con il doppio del semiasse maggiore:

$\scriptstyle \overline{PF_1} + \overline{PF_2} = 2a$

$\scriptstyle \sqrt{(x-x_1)^2+(y-y_1)^2} + \sqrt{(x-x_2)^2+(y-y_2)^2} = 2a$

Per trovare l'equazione canonica o normale dell'ellisse, con centro nell'origine e i fuochi sull'asse delle x(cioè a>b), sostituiamo y₁ = 0, y₂ = 0, x₁ = -c, x₂ = c, c = $\scriptstyle \sqrt{a^2-b^2}$. Dopo alcuni passaggi si ricava che l'ellisse centrata nell'origine di un sistema x-y di assi cartesiani con l'asse maggiore posto lungo l'asse delle ascisse è definita dall'equazione:

$\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$

La stessa ellisse è rappresentata anche dall'equazione parametrica:

$\begin{cases}x = a\,\cos t \\y = b\,\sin t \\0 \leq t < 2\pi \end{cases}$

che fa uso delle funzioni trigonometriche seno e coseno.

Eccentricità

L'eccentricità e di un'ellisse è compresa tra zero e uno ed è il rapporto della distanza tra i due fuochi F₁=(-c;0) ed F₂=(+c;0) e la lunghezza dell'asse maggiore 2a:

$e = \frac{2c}{2a} = \frac{c}{a}$

L'eccentricità rende conto della forma più o meno schiacciata dell'ellisse: quando è pari a zero, i due fuochi coincidono e l'ellisse degenera in una circonferenza di raggio a. Man mano che l'eccentricità tende a 1, l'ellisse si schiaccia sempre più e quando assume il valore unitario essa degenera in un segmento lungo 2a percorso due volte, quindi la lunghezza dell'ellisse è pari a 4a.

Coordinate polari con centro in uno dei fuochi.

Semilato retto

Il semilato retto di un'ellisse, solitamente denotato dalla lettera l, è la distanza tra ciascuno dei fuochi dell'ellisse e l'ellisse stessa misurata lungo una linea perpendicolare all'asse maggiore. È legato ad a e b dalla formula

$l = \frac{b^2}{a}$

Equazione in coordinate polari relative a uno dei fuochi

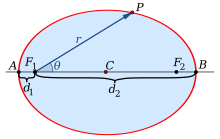
In coordinate polari, un'ellisse con un fuoco nell'origine e con la coordinata angolare $\theta$ misurata a partire dall'asse maggiore è rappresentata dall'equazione:

$r(\theta) = \frac{l} {1 - e \cos \theta}$

dove l denota il semilato retto e la coordinata angolare $\theta$ è l'angolo che la retta r passante per F1 forma con l'asse maggiore (vedi fig.).

Se si considera la retta r passante per il fuoco F2 e la coordinata angolare $\theta$ è l'angolo che la retta r passante per F2 forma con l'asse maggiore, l'equazione diviene:

$r(\theta) = \frac{l} {1 + e \cos \theta}$

Area

L'area racchiusa da un'ellisse è data da

$A = {\pi} \cdot a \cdot b$.

Tangente a un'ellisse in un suo punto: formula dello sdoppiamento

Tangente a un'ellisse in un suo punto P₀(x₀,y₀). Coefficiente angolare: $\scriptstyle \bold {m=-\frac{b^2x_0}{a^2y_0}}$
Equazione: $\scriptstyle \bold{\frac{{xx}_0}{a^2}+\frac{{yy}_0}{b^2}=1}$

L'equazione della retta tangente all'ellisse in un suo punto P₀ è:

$\frac{{xx}_0}{a^2}+\frac{{yy}_0}{b^2}=1$

Il suo coefficiente angolare è dato da:

$m=-\frac{b^2x_0}{a^2y_0}$

Dimostrazione mediante calcolo algebrico

Scriviamo un sistema di 3 equazioni, la prima è l'equazione dell'ellisse, la seconda impone l'appartenenza all'ellisse del punto P₀(x₀,y₀), la terza impone il passaggio della tangente per il punto P₀ con inclinazione m da determinare:

$\scriptstyle \begin{cases} \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \\ \scriptstyle \frac{x^2_0}{a^2}+\frac{y^2_0}{b^2}=1 \\ \scriptstyle y-y_0=m(x-x_0) \end{cases}$

Nella prima e seconda equazione i secondi membri sono uguali a 1 e quindi anche i primi membri saranno tra essi uguali:

$\scriptstyle \begin{cases} \scriptstyle \frac{x^2}{a^2}+\frac{y^2}{b^2}=\frac{x^2_0}{a^2}+\frac{y^2_0}{b^2} \\ \scriptstyle \scriptstyle y-y_0=m(x-x_0) \end{cases}$

$\scriptstyle \begin{cases}\frac{\left(x-x_0\right)\left(x+x_0\right)}{a^2}+\frac{\left(y-y_0\right)\left(y+y_0\right)}{b^2}=0 \\ \scriptstyle y-y_0=m(x-x_0) \end{cases}$

Consideriamo l'equazione della tangente:

$\scriptstyle y-y_0=m(x-x_0)$

$\scriptstyle y=m(x-x_0)+y_0$

Sostituendo nella prima equazione:

$\scriptstyle \begin{cases}\frac{\left(x-x_0\right)\left(x+x_0\right)}{a^2}+\frac{\left[m(x-x_0\right]\left[m(x-x_0)+2y_0\right]}{b^2}=0 \\ \scriptstyle y-y_0=m(x-x_0) \end{cases}$

$\scriptstyle \begin{cases}\frac{\left(x-x_0\right)\left(x+x_0\right)}{a^2}+\frac{m^2(x-x_0)^2+2y_0m(x-x_0)}{b^2}=0 \\ \scriptstyle y-y_0=m(x-x_0) \end{cases}$

$\scriptstyle \begin{cases}(x-x_0)[\frac{\left(x+x_0\right)}{a^2}+\frac{m^2(x-x_0)+2y_0m}{b^2}]=0 \\ \scriptstyle y-y_0=m(x-x_0) \end{cases}$

Per l'annullamento del prodotto:

$\scriptstyle x-x_0=0$

$\scriptstyle x=x_0$

Facilmente verificabile poiché il punto appartiene all'ellisse.

Nel secondo fattore invece:

$\scriptstyle \frac{\left(x+x_0\right)}{a^2}+\frac{m^2(x-x_0)+2y_0m}{b^2}=0$

Poiché (x-x₀)=0 e x=x₀:

$\scriptstyle \frac{{2x}_0}{a^2}+\frac{{2y}_0m}{b^2}=0$

$\scriptstyle \bold {m=-\frac{b^2x_0}{a^2y_0}}$ (coefficiente angolare della retta tangente nel punto P₀)

Sostituiamo la pendenza m nell'equazione della retta:

$\scriptstyle y-y_0=-\frac{b^2x_0}{a^2y_0}(x-x_0)$

$\scriptstyle a^2y_0y-a^2y^2_0=b^2x^2_0-b^2x_0x$

$\scriptstyle {\frac{{xx}_0}{a^2}+\frac{{yy}_0}{b^2}=\frac{x^2_0}{a^2}+\frac{y^2_0}{b^2}}$

Per ipotesi nel sistema

$\scriptstyle {\frac{x^2_0}{a^2}+\frac{y^2_0}{b^2}=1}$

Quindi:

$\scriptstyle \bold{\frac{{xx}_0}{a^2}+\frac{{yy}_0}{b^2}=1}$ (c.d.d)

Dimostrazione mediante derivate

Una dimostrazione alternativa può essere fatta ricorrendo alla derivata della "funzione" ellisse $\scriptstyle \frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ nel punto P₀: basta infatti ricordare che la derivata di una funzione in un suo punto coincide con il coefficiente angolare della retta tangente nel punto stesso. Effettuando quindi la derivata rispetto a x dell'equazione dell'ellisse otteniamo:

$\scriptstyle \frac{2x}{a^2}+\frac{2yy'}{b^2}=0$

Poiché y', come detto, coincide con la tangente, ovvero con il coefficiente angolare m, si ottiene

$\scriptstyle m=y'=-\frac{b^2x}{a^2y}$

che calcolata nel punto P₀(x₀,y₀) fornisce:

$\scriptstyle \bold{m=-\frac{b^2x_0}{a^2y_0}}$ (c.d.d)

Proprietà tangenziale

Una tangente all'ellisse in un suo punto P forma angoli uguali con le rette passanti per P e per ciascuno dei due fuochi.

Per dimostrare questa proprietà si può ricorrere al teorema di Erone in base al quale data una retta r e due punti Q ed R ad essa esterni, il punto P della retta r che minimizza la somma $\scriptstyle \overline{PQ}+\overline{PR}$ è quello per il quale i segmenti $\scriptstyle \overline{PQ}$ e $\scriptstyle \overline{PR}$ formano angoli uguali con la retta r.

Consideriamo a tale scopo un'ellisse con fuochi Q ed R: un suo qualunque punto P soddisfa la condizione

$\scriptstyle \overline{PQ}+\overline{PR}=2a$

Si tenga inoltre presente che per un qualunque punto S interno all’ellisse vale la condizione

$\scriptstyle \overline{SQ}+\overline{SR}<2a$

Consideriamo ora una retta passante per un punto P dell'ellisse tale da formare angoli uguali con i segmenti $\scriptstyle \overline{PQ}$ e $\scriptstyle \overline{PR}$: per il teorema di Erone il punto P è il punto della retta che rende minima la somma $\scriptstyle \overline{PQ}+\overline{PR}$. Ciò implica che la retta deve essere tangente all'ellisse: infatti se così non fosse, la retta entrerebbe dentro l'ellisse e detto S un suo punto ad essa interno varrebbe la condizione $\scriptstyle \overline{SQ}+\overline{SR}<2a$ in contrasto con il teorema di Erone per il quale in P e non in S si sarebbe dovuta registrare la minima somma. Resta così dimostrata l’affermazione iniziale.

Vediamo alcune conseguenze di questo enunciato.

In un tavolo da biliardo a forma di ellisse una palla lanciata da uno dei due fuochi verrà riflessa dal bordo e passerà necessariamente per l’altro fuoco. La stessa cosa si verificherà in uno specchio concavo a forma di ellisse nel quale tutti i raggi luminosi emessi da uno dei due fuochi passeranno necessariamente per l'altro fuoco indipendentemente dalla direzione seguita: da qui deriva il nome di fuochi dati a questi due particolari punti dell'ellisse. Analogamente, in una camera a forma di ellisse le onde sonore che partono da uno dei due fuochi raggiungeranno l'altro da tutte le direzioni e poiché la distanza percorsa nel tragitto da un fuoco all'altro è sempre la stessa le onde arriveranno tutte sincronizzate: questo spiega perché due persone poste nei due fuochi possono comunicare facilmente anche da lunghe distanze, mentre due persone, anche notevolmente più vicine tra loro ma non situate nei fuochi, potrebbero non sentire le parole dell’altra.

Costruzione geometrica della retta tangente a un'ellisse su un suo punto

Costruzione della retta tangente all'ellisse nel suo punto P

Si consideri una ellisse di fuochi $F_1$, $F_1$ e asse maggiore 2a e un punto P appartenente all'ellisse. Esistono due metodi grafici per tracciare la tangente in un punto P dell'ellisse.

Primo metodo

Tracciare i segmenti $PF_1$ e $PF_2$. Tracciare la bisettrice s dell'angolo $\widehat{F_1PF_2}$. Tracciare la retta t perpendicolare a s nel punto P. La retta t è la retta tangente cercata.

Basta dimostrare che tale retta soddisfa la proprietà tangenziale precedentemente descritta. Infatti gli angoli $\beta_2$ e $\beta_3$ sono congruenti in quanto differenza di angoli rispettivamente congruenti (ai due angoli retti sono sottratti gli angoli $\alpha_1$ e $\alpha_2$ congruenti per la bisettrice)

Secondo metodo

Tracciare la circonferenza di centro $F_1$ e raggio $2a$. Tracciare il segmento $F_1P$ e prolungarlo fino ad incontrare il punto E sulla circonferenza. Tracciare $PF_2$. Tracciare il segmento $EF_2$. Fissare il punto medio M di $EF_2$. La retta t passante per i punti M e P è la retta tangente cercata.

È possibile infatti dimostrare che tale retta soddisfa la proprietà tangenziale precedentemente descritta. $PF_2=PE$ in quanto differenza di segmenti congruenti ($EP+PF_1=2a$ e $PF_1+PF_2=2a$. Quindi il triangolo $PEF_2$ è isoscele e la mediana $PM$ relativa alla base $EF_2$ è anche bisettrice e dunque gli angoli $\beta_1$ e $\beta_2$ sono congruenti. D'altra parte gli angoli $\beta_1$ e $\beta_3$ sono congruenti in quanto opposti al vertice. E quindi $\beta_2$ e $\beta_3$ sono congruenti per la proprietà transitiva.

Tangenti a un'ellisse condotte da un punto esterno

Tangenti a un'ellisse condotte da un punto P₀(x₀,y₀) ad essa esterno. I coefficienti angolari delle due rette si ottengono risolvendo l'equazione di secondo grado:
$\scriptstyle \bold {\left(a^2-x^2_0\right)m^2+2x_0y_0m+b^2-y^2_0=0}$

I coefficienti angolari delle tangenti a un'ellisse condotte da un punto P₀(x₀,y₀) ad essa esterno si ricavano dalla risoluzione della seguente equazione di secondo grado:

$\left(a^2-x^2_0\right)m^2+2x_0y_0m+b^2-y^2_0=0$

Dimostrazione

Scriviamo il sistema di due equazioni con la prima relativa all'equazione dell'ellisse e la seconda relativa al fascio di rette passanti per il punto P₀

$\begin{cases} \scriptstyle \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \\ \scriptstyle y-y_0=m(x-x_0) \end{cases}$

$\begin{cases} \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \\ \scriptstyle y=mx-{mx}_0+\ y_0 \end{cases}$

Sostituiamo la seconda nella prima:

$\scriptstyle \frac{x^2}{a^2}+\frac{m^2x^2+m^2x^2_0+y^2_0-2m^2x_{0\ }x+2my_0x-2mx_0y_0}{b^2}-1=0$

$\scriptstyle \left(\frac{1}{a^2}+\frac{m^2}{b^2}\right)x^2+\left(-\frac{2x_0m^2}{b^2}+\frac{2y_0m}{b^2}\right)x+\left(\frac{x^2_0m^2}{b^2}-\frac{2x_0y_0m}{b^2}+\frac{y^2_0-b^2}{b^2}\right)=0$

Imponiamo ora la condizione di tangenza, ovvero che il discriminante Δ si annulli facendo questa espressione :

$\scriptstyle {\left(-\frac{2x_0m^2}{b^2}+\frac{2y_0m}{b^2}\right)}^2-4\left(\frac{1}{a^2}+\frac{m^2}{b^2}\right)\left(\frac{x^2_0m^2}{b^2}-\frac{2x_0y_0m}{b^2}+\frac{y^2_0-b^2}{b^2}\right)=0$

$\scriptstyle \cancel{\frac{4m^4x^2_0}{b^4}}-\cancel{\frac{8m^3x_0y_0}{b^4}}+\frac{4m^2y^2_0}{b^4}-4\left(\frac{x^2_0m^2}{a^2b^2}-\frac{2x_0y_0m}{a^2b^2}+\frac{y^2_0-b^2}{a^2b^2}+\cancel{\frac{x^2_0m^4}{b^4}}-\cancel{\frac{2x_0y_0m^3}{b^4}}+\frac{\left(y^2_0-b^2\right)m^2}{b^4}\right) =0$

$\scriptstyle \frac{4y^2_0m^2}{b^4}-\frac{4x^2_0m^2}{a^2b^2}-\frac{4\left(y^2_0-b^2\right)m^2}{b^4}+\frac{8x_0y_0m}{a^2b^2}-\frac{4\left(y^2_0-b^2\right)}{a^2b^2}=0$

$\scriptstyle \cancel{4a^2y^2_0m^2}-4{b^2x}^2_0m^2-4a^2\left(\cancel{y^2_0}-b^2\right)m^2+8{b^2x}_0y_0m-4b^2\left(y^2_0-b^2\right)=0$

$\scriptstyle -x^2_0m^2+a^2m^2\ +2x_0y_0m-y^2_0+b^2=0$

$\scriptstyle \left(a^2-x^2_0\right)m^2+2x_0y_0m+b^2-y^2_0=0$ (c.d.d.)

Costruzione geometrica delle rette tangenti ad una ellisse condotte da un punto esterno

Rette tangenti ad una ellisse condotte da un punto esterno P

È data una ellisse di fuochi $F_1$, $F_2$ e asse maggiore 2a, e un punto P esterno all'ellisse. Esistono due metodi per tracciare le rette tangenti all'ellisse condotte dal punto esterno P.

Primo metodo

Tracciare la circonferenza di centro $F_1$ e raggio $2a$. Tracciare la circonferenza di centro P e raggio $PF_2$. Le due circonferenze si intersecano nei punti A e B. Tracciare i segmenti $F_1A$ e $F_1B$. Fissare i punti T ed S di intersezione tra i due segmenti e l'ellisse. Le rette PT e PS sono le rette tangenti cercate.

Basta dimostrare infatti che tali rette soddisfano la proprietà tangenziale sopra descritta. Anzitutto si osserva che i triangoli $TAP$ e $TF_2P$ sono congruenti perché hanno i tre lati ordinatamente congruenti: $TP$ è in comune, $PA=PF_2$ perché raggi della stessa circonferenza e $TA=F_2T$ in quanto differenze di segmenti rispettivamente congruenti, infatti $TF_1+TF_2=2a$ e $TF_1+TA=2a$. In particolare gli angoli $\widehat{ATP}=\widehat{F_2TP}$. D'altra parte anche gli angoli $\widehat{tTF_1}=\widehat{ATP}$ e quindi la proprietà tangenziale è dimostrata.

Secondo metodo

Tracciare la circonferenza di centro $F_1$ e raggio $2a$. Tracciare la circonferenza di centro P e raggio $PF_2$. Le due circonferenze si intersecano nei punti A e B. Tracciare i segmenti $F_2A$ e $F_2B$. Condurre per P la retta t perpendicolare al segmento $F_2A$. Condurre per P la retta s perpendicolare al segmento $F_2B$. Le rette t ed s sono le rette tangenti cercate.

Dalla dimostrazione precedente si osserva che TP è bisettrice dell'angolo al vertice del triangolo isoscele $ATF_2$ e quindi è anche altezza.

Equazione generale di un'ellisse

L'equazione generale dell'ellisse avente i fuochi F₁(x_F1;y_F1) ed F₂(x_F2;y_F2) posti in posizione generica sul piano cartesiano e avente il semiasse maggiore denotato con a è data da

$Ax^2+Bxy+Cy^2+Dx+Ey+F=0$

dove i parametri A, B, C, D, E ed F sono pari a

$\scriptstyle A=16a^2-4(x_{F1}-x_{F2})^2$

$\scriptstyle B=-8(x_{F1}-x_{F2})(y_{F1}-y_{F2})$

$\scriptstyle C=16a^2-4(y_{F1}-y_{F2})^2$

$\scriptstyle D=4(x_{F1}-x_{F2})(x_{F1}^2-x_{F2}^2+y_{F1}^2-y_{F2}^2)-16a^2(x_{F1}+x_{F2})$

$\scriptstyle E=4(y_{F1}-y_{F2})(x_{F1}^2-x_{F2}^2+y_{F1}^2-y_{F2}^2)-16a^2(y_{F1}+y_{F2})$

$\scriptstyle F=4(x_{F1}^2+y_{F1}^2)(x_{F2}^2+y_{F2}^2)-(x_{F1}^2+x_{F2}^2+y_{F1}^2+y_{F2}^2-4a^2)^2$

Lunghezza

La lunghezza dell'ellisse è $c = 4 a E(e^2)$, dove la funzione E è un integrale ellittico completo di seconda specie.

Lo sviluppo in serie è:

$\scriptstyle c = 2\pi a \left[{1 - \left({1\over 2}\right)^2e^2 - \left({1\cdot 3\over 2\cdot 4}\right)^2{e^4\over 3} - \left({1\cdot 3\cdot 5\over 2\cdot 4\cdot 6}\right)^2{e^6\over5} - \dots}\right]$

Una buona approssimazione è quella di Ramanujan:

$\scriptstyle c \approx \pi \left[3(a+b) - \sqrt{(3a+b)(a+3b)}\right]$

che può anche essere scritta come:

$\scriptstyle c \approx \pi a \left[ 3 (1+\sqrt{1-e^2}) - \sqrt{(3+ \sqrt{1-e^2})(1+3 \sqrt{1-e^2})} \right]$

Un'altra formula approssimata è la seguente:

l=(1-e^2)/arcsin(1-e^2):

che ha il vantaggio sulla precedente di essere più precisa per e->1, ma lo svantaggio di dovere calcolare o consultare le tavole della funzione arcoseno.

Più in generale, la lunghezza dell'arco di una porzione di ellisse, come funzione dell'angolo sotteso, è data da un integrale ellittico incompleto. La funzione inversa, l'angolo sotteso come funzione della lunghezza dell'arco, è data da una funzione ellittica.

Costruzione dell'ellisse

Metodo della tangente per la costruzione geometrica dell'ellisse

Metodo della tangente

Fissare i due fuochi $F_1$ e $F_2$ e l'asse maggiore di lunghezza 2a ($2a > F_1F_2$). Costruire una circonferenza di centro $F_1$ e raggio 2a. Fissare sulla circonferenza un punto generico K. Tracciare il raggio $F_1K$. Tracciare il segmento $F_2K$ e l'asse di tale segmento (retta perpendicolare al segmento passante per il suo punto medio M) che interseca $F_1K$ nel punto P. Il punto P è equidistante da $F_2$ e da K in quanto sta sull'asse del segmento $F_2K$. Dunque $PF_2 = PK$. D'altra parte $PF_1+PK=2a$ e quindi $PF_1+PF_2=2a$. P è un punto dell'ellisse. Questo metodo viene detto della tangente in quanto la retta MP è la tangente all'ellisse nel punto P, infatti gode della proprietà tangenziale, precedentemente descritta.

Metodo del giardiniere

In questo caso sono note le lunghezze degli assi che danno il rettangolo di ingombro (rettangolo che contiene l'ellisse). Il metodo è ben descritto nell'Ellisse_del_giardiniere; per meglio capire questo sistema come funzioni, basta immaginare che la linea rossa nella figura qui accanto sia la corda utilizzata dal "giardiniere" per tracciare l'ellisse.

Film

• Nel film Agorà del 2009, Ipazia, interpretata dalla bellissima Rachel Weisz, studiando l'orbita della Terra attorno al Sole, traccia sulla sabbia un'ellisse con il metodo del giardiniere. In alcuni momenti si vede anche un cono di Apollonio. Qui si possono vedere entrambe le scene.

Voci correlate

• Coordinate ellittiche
• Diametro coniugato
• Ellisse del giardiniere
• Ellissoide, un'ellisse in tre o più dimensioni.
• Iperbole (geometria)
• Orbita ellittica
• Parabola (geometria)
• Rappresentazione matriciale delle coniche
• Sezione conica
• Sferoide, l'ellissoide ottenuto ruotando un'ellisse attorno al suo asse maggiore o minore.
• Superellisse, una generalizzazione dell'ellisse, è più squadrata.

Altri progetti

• Wikizionario
• Commons

• Wikizionario contiene il lemma di dizionario «Ellisse»
• Commons contiene immagini o altri file su Ellisse

Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica