Teorema diretto dei triangoli isosceli
In geometria euclidea, il teorema diretto dei triangoli isosceli, noto anche come pons asinorum, afferma che gli angoli opposti ai due lati uguali di un triangolo isoscele sono congruenti. Si tratta, in sostanza, del contenuto della proposizione 5 nel libro I degli Elementi di Euclide.
Pons asinorum[modifica | modifica wikitesto]
Il teorema viene a volte indicato come pons asinorum (termine latino per "ponte degli asini"). Ci sono due possibili spiegazioni per il nome: la più semplice è che lo schema utilizzato per la dimostrazione assomiglia a un ponte vero e proprio. Ma la spiegazione più popolare è che negli Elementi esso rappresenta il primo vero test dell'intelligenza del lettore, come un ponte verso le proposizioni più difficili che seguono.[1] Qualunque sia la sua origine, il termine pons asinorum è usato come metafora per un problema o una sfida che separerà i sicuri di mente dai semplici, il pensatore agile dal lento, il determinato dall'esitante: rappresenta un test critico per verificare la capacità o comprensione.[2] Un altro termine medievale per il teorema è stato Elefuga che, secondo Ruggero Bacone, deriva dal greco elegia miseria, e dal latino fuga, cioè "fuga dei miserabili". Anche quest'etimologia è dubbia, e vi fa riferimento Chaucer al termine " fuga dei miserabili" (in inglese "flemyng of wreches") per il teorema.[3]
Uso metaforico[modifica | modifica wikitesto]
Gli usi del termine o del teorema come metafora includono:
- Il Philobiblon di Richard Aungerville contiene il passaggio "Quot Euclidis discipulos retrojecit Elefuga quasi scopulos eminens et abruptus, qui nullo scalarum suffragio scandi posset! Durus, inquiunt, est hie sermo; quis potest eum audire?" nel quale si paragona il teorema ad una ripida scogliera che nessuna scala può aiutare a scalare e si chiede quanti aspiranti geometri ne sono fuggiti.[3]
- Il termine pons asinorum, in entrambi i suoi significati, come ponte e come test è usato come metafora per trovare il termine medio di un sillogismo.[3]
- Nel libro Vita di Giovambattista Vico scritta da se medesimo, il filosofo Giovambattista Vico racconta che egli "volle applicarsi alla geometria e inoltrarsi fino alla quinta proposizione di Euclide" con i seguenti esiti: "a suo costo sperimentò che alle menti già dalla metafisica fatte universali non riesce agevole quello studio proprio degli ingegni minuti, e lasciò di seguitarlo".
- Nel XVIII secolo, il poeta Thomas Campbell scrisse un poema umoristico dal titolo The Pons asinorum dove una classe di geometria assale il teorema come una compagnia di soldati potrebbero caricare una fortezza; la battaglia non priva di incidenti.[4]
- L'economista John Stuart Mill definì la Teoria della rendita di Ricardo il Pons Asinorum dell'economia.[5]
- Pons Asinorum è il nome dato ad una particolare configurazione del cubo di Rubik.[6]
Dimostrazioni[modifica | modifica wikitesto]
Euclide e Proclo[modifica | modifica wikitesto]

L'enunciato del teorema di Euclide include una seconda conclusione, che se i lati uguali del triangolo sono prolungati sotto la base, allora gli angoli tra le estensioni e la base sono uguali. La dimostrazione di Euclide consiste nel definire le linee ausiliarie per queste estensioni. Ma, nel commentare Euclide, Proclo mette in evidenza che Euclide non usa mai la seconda conclusione e la sua dimostrazione può essere semplificata in qualche modo tracciando le linee ausiliarie ai lati del triangolo, mentre il resto della dimostrazione si esegue più o meno allo stesso modo. Ci sono state molte speculazioni e dibattiti sul perché Euclide abbia aggiunto la seconda conclusione al teorema, dal momento che rende la dimostrazione più complicata. Una spiegazione plausibile, data da Proclo, è che la seconda conclusione possa essere utilizzata in eventuali obiezioni alle dimostrazioni successive di proposizioni in cui Euclide non copre tutti i casi.[7] La dimostrazione si basa su quello che è oggi chiamato Lato-Angolo-Lato, ovvero la proposizione precedente negli Elementi.

La variante di Proclo alla dimostrazione di Euclide procede come segue:[8] sia un triangolo isoscele con e i lati uguali. Si scelga un punto arbitrario sul lato e si prenda il punto su in modo che . Tracciate le linee di , e si consideri i triangoli e , questi triangoli hanno , , e l'angolo coincidente, quindi per il criterio di congruenza lato-angolo-lato i triangoli e sono congruenti e pertanto i lati e gli angoli corrispondenti saranno congruenti: l'angolo è uguale all'angolo , l'angolo è uguale all'angolo , e .
Dal momento che e , per sottrazione di parti uguali. Si consideri ora i triangoli e ; per essi , , e l'angolo è uguale all'angolo come è stato appena mostrato, quindi ancora per il criterio lato-angolo-lato, i triangoli sono congruenti: l'angolo è uguale all'angolo . (La congruenza implica anche , ma questo è evidente).
Poiché l'angolo è uguale all'angolo e l'angolo è uguale all'angolo , allora l'angolo sarà uguale all'angolo per sottrazione di parti uguali.
Consideriamo una terza coppia di triangoli, e ; , , e l'angolo uguale all'angolo , quindi applicando lato-angolo-lato una terza volta, si dimostra che i due triangoli sono congruenti. In particolare, l'angolo , come volevasi dimostrare.
Pappo[modifica | modifica wikitesto]
Proclo presenta una dimostrazione molto più corta attribuita a Pappo di Alessandria. Essa non è solo più semplice, ma non richiede costruzioni aggiuntive. Il metodo di dimostrazione applicato è il criterio lato-angolo-lato tra un triangolo e la sua immagine speculare. Altri autori moderni, descrivono questo metodo di dimostrazione come prendere il triangolo, capovolgerlo e posarlo su se stesso.[9] Questo metodo è oggetto di satira da parte di Charles Dodgson in Euclide e i suoi rivali moderni, che lo definisce un "Irish bull", ovverosia un non senso, poiché apparentemente richiede che il triangolo si trovi in due posti contemporaneamente.[10]
La dimostrazione è la seguente:[11] Sia un triangolo isoscele con e i suoi due lati congruenti. Si considerino i triangoli e , dove è un secondo triangolo con vertici , e corrispondenti rispettivamente ai vertici , e nel triangolo originale. Si avrà , e l'angolo uguale a se stesso, così per il criterio lato-angolo-lato, i triangoli e sono congruenti. In particolare l'angolo è congruente all'angolo .[12]
Altro[modifica | modifica wikitesto]
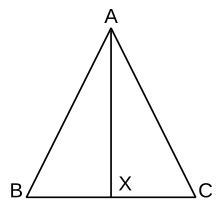
La dimostrazione standard dei libri di testo consiste nel costruire la bisettrice dell'angolo .[13] Questa è più semplice della dimostrazione di Euclide, ma Euclide non presenta la costruzione della bisettrice di un angolo prima della proposizione 9. Così l'ordine della presentazione delle proposizioni di Euclide deve essere cambiato per evitare un ragionamento circolare.
La dimostrazione procede come segue:[14] come prima consideriamo il triangolo con . Costruiamo la bisettrice dell'angolo e prolunghiamola fino a incontrare il lato nel punto . Nei triangoli e si ha , coincidente. Inoltre l'angolo , così, per il criterio lato-angolo-lato, e sono congruenti. Segue che gli angoli e sono congruenti.
Legendre usa una costruzione simile in Éléments de géométrie, ma considerando il punto X come punto medio del segmento BD.[15] La dimostrazione è simile ma usa il criterio Lato-Lato-Lato al posto di lato-angolo-lato, ma lato-lato-lato non è mostrato che molto più avanti da Euclide negli Elementi.
Prodotto interno[modifica | modifica wikitesto]
Il teorema diretto dei triangoli isosceli equivale al prodotto interno su numeri reali o complessi. In questi spazi equivale a prendere dei vettori , e tali che[16]
quindi
Mentre
e
dove è l'angolo tra i due vettori, la conclusione di questa forma del teorema equivale a enunciare l'uguaglianza degli angoli.
Note[modifica | modifica wikitesto]
- ^ David Eugene Smith, History of Mathematics, New York, Dover publications, 1958, p. 284.
- ^ (EN) Merriam-Webster, Definition of Pons asinorum, su merriam-webster.com. URL consultato il 9 dicembre 2012 (archiviato il 20 febbraio 2010).
- ^ a b c A. F. West, H. D. Thompson, On Dulcarnon, Elefuga And Pons Asinorum as Fanciful Names For Geometrical Propositions, in The Princeton University bulletin, vol. 3, n. 4, 1891, p. 84.
- ^ (EN) Thomas Campbell, William Edmondstoune Aytoun, The poetical works of Thomas Campbell, Little, Brown, 1864, p. 385.
- ^ (EN) Henry Dunning Macleod, On rent, in The Elements of Economics, vol. 2, Londra, Longmans, 1886, p. 96. URL consultato il 9 dicembre 2012.«Mills goes so far as to call Ricardo's Teory of Rent the pons asinorum of Economics.»
- ^ Rubik's Cube patterns Archiviato il 12 dicembre 2012 in Archive.is.
- ^ Heath pp. 251-255
- ^ Secondo Proclo p. 53
- ^ Francis Cuthbertson, Primer of geometry, 1876, p. 7. URL consultato il 9 dicembre 2012.
- ^ Charles Lutwidge Dodgson, Euclide e i suoi rivali moderni Act I Scene II §6
- ^ Secondo Proclo p. 54
- ^ Heath p. 254 for section
- ^ Per esempio J.M. Wilson Elementary geometry (1878 Oxford) p. 20
- ^ Following Wilson
- ^ A. M. Legendre Éléments de géométrie (1876 Libr. de Firmin-Didot et Cie) p. 14
- ^ J. R. Retherford, Hilbert Space, Cambridge University Press, 1993, page 27.
Bibliografia[modifica | modifica wikitesto]
- Euclide, commento e traduzione di T. L. Heath Elements Vol. 1 (1908 Cambridge) Google Books
- Euclide, commento di Proclo, traduzione inglese di T. Taylor Elements Vol. 2 (1789) Google Books
- Proclus, A Commentary on the First Book of Euclid’s Elements, Princeton, Princeton University Press, 1970
- John Stillwell, The Four Pillars of Geometry, Springer, 2005, p. 24.
Voci correlate[modifica | modifica wikitesto]
Collegamenti esterni[modifica | modifica wikitesto]
- (EN) pons asinorum, in PlanetMath.
























































