Orbita omoclina

In matematica, una orbita omoclina è una traiettoria di un flusso di un sistema dinamico che unisce un punto di equilibrio a sella a se stesso. Più precisamente, una orbita omoclina si trova nell'intersezione della varietà stabile e della varietà instabile di un punto di equilibrio. Orbite omocline e punti omoclinici sono definiti nello stesso modo per le funzioni ricorsive, come intersezione dell'insieme stabile e di quello instabile di un qualche punto fisso o punto periodico del sistema.

Si consideri il sistema dinamico continuo descritto dall'equazione differenziale ordinaria:

{\dot {x}}=f(x)

Supponendo che ci sia un punto di equilibrio a $x=x_{0}$ , allora una soluzione $\Phi (t)$ è una orbita omoclina se:

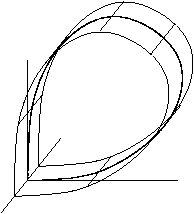
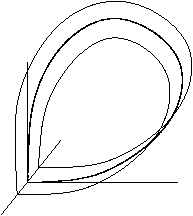
\phi (t)\to x_{0}\quad \mathrm {se} \quad t\to \pm \infty

Se lo spazio delle fasi ha tre o più dimensioni, allora è importante considerare la topologia della varietà instabile del punto di sella. Le figure mostrano questi due casi. La prima, quando la varietà instabile è topologicamente un cilindro e l'orbita omoclina è detta orientata, e la seconda, dove la varietà instabile è topologicamente un Nastro di Möbius, in questo caso l'orbita omoclina è chiamata twistata (twisted).

Si ha anche la nozione di orbita omoclina quando si considera in sistema dinamico discreto. In questo caso, se $f:M\rightarrow M$ è un diffeomorfismo della varietà $M$ , si dice che $x$ è un punto omoclinico se ha stesso passato e futuro - più precisamente se esiste un punto fisso (o periodico) $p$ tale che:

\lim _{n\rightarrow \pm \infty }f^{n}(x)=p

Bibliografia[modifica | modifica wikitesto]

(EN) Edward Ott, Chaos in Dynamical Systems, Cambridge University Press, 1994.
(EN) Stephen Smale, Differentiable dynamical systems, Bull. Amer. Math. Soc.73, 747-817, 1967.
(EN) John Guckenheimer, Philip Holmes; Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields, Applied Mathematical Sciences Vol. 42, Springer