Formula dell'area di Gauss

La formula dell'area di Gauss, che prende il nome dal matematico tedesco Carl Friedrich Gauss, è una formula matematica utilizzata per determinare l'area di un poligono i cui vertici siano descritti in coordinate cartesiane.

Formula

La formula può essere rappresentata dall'espressione:

$A={1 \over 2}|x_{1}y_{2}+x_{2}y_{3}+\ldots +x_{n-1}y_{n}+x_{n}y_{1}-x_{2}y_{1}-x_{3}y_{2}-\ldots -x_{n}y_{n-1}-x_{1}y_{n}|,$

dove

• $A$ è l'area del poligono,
• $n$ il numero di lati
• $(x_{i},y_{i})$, con $i=1,\ldots ,n$ sono i vertici del poligono.

Oppure, servendosi delle sommatorie:

$A={\frac {1}{2}}\left|\sum _{i=1}^{n}(x_{i}y_{i+1}-x_{i+1}y_{i})\right|$, dove $x_{n+1}$ e $y_{n+1}$ indicano rispettivamente $x_{1}$ e $y_{1}$.

Dimostrazione

La dimostrazione della formula si basa sul concetto di forma differenziale: il calcolo dell'area della figura è infatti la generalizzazione dell'integrazione utilizzata per il calcolo di una superficie.

Sia $\Omega$ l'insieme dei punti $P(x,y)$ appartenenti al poligono.

L'area è $A=\int _{\Omega }\alpha$, dove $\alpha$ è una 2-forma definita come $\alpha =dx\wedge dy$.

Sia $d\omega =\alpha$, con

$\omega ={\frac {x\,dy}{2}}-{\frac {y\,dx}{2}}.$

Grazie a questa sostituzione,

$\int _{\Omega }\alpha =\int _{\Omega }d\omega$

ma, per il teorema di Green risulterà:

$\int _{\Omega }d\omega =\int _{\partial \Omega }\omega .$

Il bordo $\partial \Omega$ della varietà considerata corrisponde all'unione dei segmenti che uniscono i vari punti: $\partial \Omega =\bigcup A(i),$ dove $A(i)$ è il segmento che unisce il punto $(x_{i},y_{i})$ a $(x_{i+1},y_{i+1})$.

Perciò

$\int _{\partial \Omega }\omega =\sum _{i=1}^{n}\int _{A(i)}\omega .$

Sostituendo per $\omega$, sarà

$\sum _{i=1}^{n}\int _{A(i)}\omega ={\frac {1}{2}}\sum _{i=1}^{n}\int _{A(i)}{x\,dy}-{y\,dx}$

e, parametrizzando,

${\frac {1}{2}}\sum _{i=1}^{n}\int _{0}^{1}{(x_{i}+(x_{i+1}-x_{i})t)(y_{i+1}-y_{i})}-{(y_{i}+(y_{i+1}-y_{i})t)(x_{i+1}-x_{i})\,dt}.$

L'integrazione porta al risultato

${\frac {1}{2}}\sum _{i=1}^{n}{\frac {1}{2}}[(x_{i}+x_{i+1})(y_{i+1}-y_{i})-(y_{i}+y_{i+1})(x_{i+1}-x_{i})],$

che, semplificato con un po' di algebra elementare è

${\frac {1}{2}}\sum _{i=1}^{n}(x_{i}y_{i+1}-x_{i+1}y_{i}).$

Q.E.D.

Esempi

Si prenda un triangolo con vertici di coordinate $\{(2,1),(4,5),(7,8)\}$. Si prenda la prima $x$ e la si moltiplichi per la seconda $y$ e così via. Si arriverà alla formula

$A_{\text{tri}}={1 \over 2}|x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1}-x_{2}y_{1}-x_{3}y_{2}-x_{1}y_{3}|,$

dove $x_{n}$ e $y_{n}$ rappresentano le coordinate di un punto. Ma questo vale solo per i triangoli. Usando la formula, si trova che l'area del triangolo descritto sopra è uguale al valore assoluto della metà di $10+32+7-4-35-16$, che è uguale a $3$.

E così l'area del pentagono diventerà

$A_{\text{pent}}={1 \over 2}|x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{4}+x_{4}y_{5}+x_{5}y_{1}-x_{2}y_{1}-x_{3}y_{2}-x_{4}y_{3}-x_{5}y_{4}-x_{1}y_{5}|,$

e per il quadrilatero sarà

$A_{\text{quad}}={1 \over 2}|x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{4}+x_{4}y_{1}-x_{2}y_{1}-x_{3}y_{2}-x_{4}y_{3}-x_{1}y_{4}|.$

Si consideri il poligono di vertici $(3,4)$, $(5,11)$, $(12,8)$, $(9,5)$ e $(5,6)$ illustrato qui sotto:

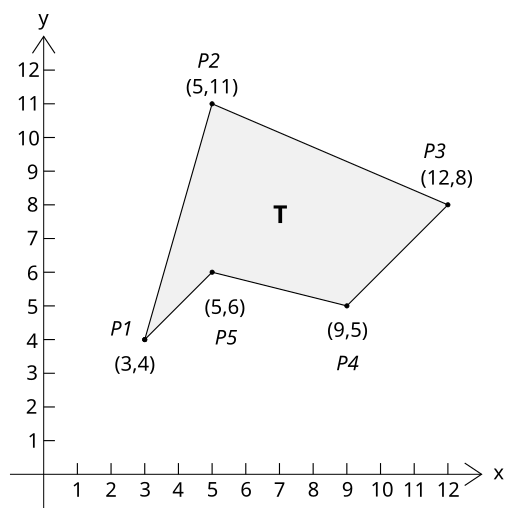
L'area del poligono vale:

${\begin{aligned}\mathbf {A} &={1 \over 2}|3\times 11+5\times 8+12\times 5+9\times 6+5\times 4\\&{}\qquad {}-4\times 5-11\times 12-8\times 9-5\times 5-6\times 3|\\[10pt]&={60 \over 2}=30\end{aligned}}$

Utilizzo con le matrici

Se si costruisce una matrice rettangolare dove siano indicate, su ogni riga, le coordinate di ogni vertice, avendo cura di riportare il primo vertice alla fine della lista, l'applicazione della formula risulterà notevolmente più semplice.

Sia il triangolo $(2,4)$, $(3,-8)$, $(1,2)$. La matrice da utilizzare sarà:

${\begin{bmatrix}2&4\\3&-8\\1&2\\2&4\end{bmatrix}}$

Innanzitutto si disegneranno dei trattini che uniscano, in diagonale i punti da sinistra a destra verso il basso, e viceversa (da destra a sinistra sempre verso il basso)

e si moltiplicheranno i due numeri connessi dalle linee, poi si calcolerà la somma dei prodotti

$2\cdot (-8)+3\cdot 2+1\cdot 4=-6.$

Lo stesso andrà fatto con le diagonali secondarie.

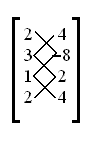
da cui si ha

$4\cdot 3+(-8)\cdot 1+2\cdot 2=8.$

Ora i due numeri vanno sottratti tra loro, e va considerato il valore assoluto della differenza (non esistono aree negative!): $|-6-8|=14$. Infine, dimezzando il risultato si ottiene l'area: $7$.

Da questo sistema la formula prende il nome del "laccio di scarpa": infatti i trattini disegnati sulla matrice sembrano proprio i lacci di una scarpa.

Fonti

(EN) Shoelace Theorem, su artofproblemsolving.com.