Utilità (economia)
In economia l'utilità è la misura della felicità o soddisfazione individuale. Un bene è dunque utile se considerato idoneo a soddisfare una domanda.[1]
Secondo l'utilitarismo, la massimizzazione dell'utilità sociale dovrebbe essere il fine ultimo della società, che dovrebbe quindi tendere ad ottenere "la felicità maggiore per il maggior numero di individui".
Utilità cardinale e ordinale[modifica | modifica wikitesto]
In economia, l'utilità individuale era implicitamente assunta come una quantità misurabile e addizionabile. Il principio di massima felicità sopra accennato era infatti commisurato alla possibilità di:
- misurare l'utilità di ciascun individuo ricollegabile a qualsiasi evento, ed in particolare al consumo di quantità date di beni e servizi;
- sommare le utilità individuali per ottenere l'utilità totale della collettività.
Questa nozione di utilità, come una quantità misurabile e aggregabile tra gli individui, è stata poi denominata utilità cardinale. Secondo tale nozione ciascun individuo è in grado di assegnare un valore esatto a ciascun bene su una scala cardinale.
Per superare le critiche mosse da più parti[senza fonte], a partire dai contributi di Vilfredo Pareto, gli economisti neoclassici svilupparono il concetto di utilità ordinale, per la quale si argomentò[senza fonte] che l'unica cosa realmente necessaria alla fondazione della teoria del valore e della teoria del consumo neoclassiche era la possibilità che gli individui potessero disporre su una scala ordinale i diversi beni in base alle loro preferenze, quindi contava solo l'ordine, non la grandezza assoluta dell'utilità.
Così, ad esempio, se l'utilità fosse intesa in senso cardinale e un individuo attribuisse utilità 10 ad una tazza di caffè e utilità 2 ad un bicchiere di aranciata, questo starebbe a significare che l'individuo preferisce cinque volte di più la tazza di caffè all'aranciata; laddove l'utilità venisse invece intesa in senso ordinale, l'unica cosa che potrebbe essere detta circa le preferenze dell'individuo in questione, sarebbe che egli preferisce il caffè all'aranciata, senza con questo quantificare in termini assoluti tale preferenza.
Funzione di utilità[modifica | modifica wikitesto]
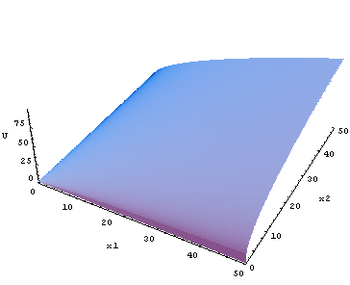
Si consideri un insieme di consumo , cioè l'insieme di tutte le possibili combinazioni di consumo individuale, e una relazione , detta di preferenza debole, su : significa cioè che un consumatore le cui preferenze sono rappresentate da , posto di fronte alla scelta tra e , preferirà o sarà indifferente tra le due opzioni. Si stabilisce così un ordinamento degli elementi dell'insieme . Sia inoltre caratterizzata dalle seguenti proprietà:
- Completezza: si ha oppure ;
- Transitività: , .
Sotto tali ipotesi, si definisce una relazione di preferenza razionale (in linguaggio matematico preordine totale); si dimostra inoltre che, sotto l'ulteriore ipotesi di continuità di detta relazione, è possibile rappresentare attraverso una funzione di utilità, una funzione cioè che leghi il consumo di beni al livello di utilità. È banale osservare che l'ipotesi di completezza implica la riflessività della relazione : ossia si ha .
In termini formali, sotto l'ipotesi che ci siano beni di consumo, l'insieme di consumo si riduce allo spazio euclideo . Qualsiasi paniere consumato è un vettore di dimensione . Una generica funzione di utilità è definita come:
tale che se e solo se .
In particolare, tale funzione sarà unica a meno di una trasformazione monotona crescente; in altri termini, se è una funzione di utilità che rappresenta le preferenze e è una funzione monotona crescente, allora anche rappresenta le preferenze . Tale proprietà implica la natura ordinale dell'ordinamento stabilito in termini di utilità - per cui non ha significato affermare che un consumatore trae dal consumo del paniere un'utilità doppia rispetto a quella che ottiene dal consumo del paniere .
Nella teoria economica vengono utilizzate diverse specificazioni della funzione di utilità:
- funzioni di utilità Cobb-Douglas;
- funzioni di utilità CES (Constant Elasticity of Substitution);
- funzioni di utilità CRRA (Constant Relative Risk Adversion);
- funzioni di utilità CARA (Constant Absolute Risk Adversion).
Note[modifica | modifica wikitesto]
- ^ Va notato che, secondo questa definizione, anche una sigaretta può essere considerata utile, nonostante i danni alla salute che ne possono derivare, se l'individuo la vuole.
Bibliografia[modifica | modifica wikitesto]
- David M. Kreps, A course in microeconomic theory, Princeton University Press, 1990, ISBN 0-691-04264-0, OCLC 20453270. (traduzione italiana: David M. Kreps, Corso di microeconomia, Il mulino, 1993, ISBN 88-15-03876-0, OCLC 797753850.)
- French, Simon (1993): Decision Theory, Ellis Horwood, New York, 1993.
- Kreps, David Mark (1998) Notes on the Theory of Choice, Underground Classics in Economics, Westview Press, Boulder (CO), USA.
- Fishburn, Peter C. (1979): Utility Theory for Decision Making, Krieger, Huntington (NY). Prima edizione (1970): Wiley, New York, in inglese.
- Andreu Mas-Colell, Michael Whinston e Jerry Green, Microeconomic theory, Oxford University Press, 1995, ISBN 0-19-507340-1, OCLC 32430901.
- Georges Bataille e Felice Ciro Papparo, Il limite dell'utile, Adelphi, 2000, ISBN 88-459-1530-1, OCLC 797696174.
- Thomas Rawson Birks, Modern Utilitarianism; Or, the Systems of Paley, Bentham, and Mill Examined and Compared, Nabu Press, 2010, ISBN 1143064550.
Voci correlate[modifica | modifica wikitesto]
Altri progetti[modifica | modifica wikitesto]
 Wikimedia Commons contiene immagini o altri file su utilità
Wikimedia Commons contiene immagini o altri file su utilità
Collegamenti esterni[modifica | modifica wikitesto]
- (EN) William J. Baumol, utility and value, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
| Controllo di autorità | Thesaurus BNCF 47415 · GND (DE) 4172189-5 |
|---|


















