Sfera di Riemann

La sfera di Riemann è ottenuta aggiungendo al piano complesso un "punto all'infinito". La proiezione stereografica mostra che lo spazio ottenuto è effettivamente una sfera.

In matematica e più precisamente in analisi complessa, la sfera di Riemann è una particolare superficie di Riemann, definita aggiungendo un "punto all'infinito" al piano complesso. È anche chiamata retta proiettiva complessa, in simboli $\mathbb {P} ^{1}(\mathbb {C} ),$ o piano complesso esteso, in simboli ${\hat {\mathbb {C} }}=\mathbb {C} \cup \{\infty \}.$

È possibile quindi vedere la sfera di Riemann da diverse prospettive tra loro complementari. A livello algebrico si considera il punto all'infinito come risultato dell'operazione

${\frac {1}{0}}=\infty .$

In questo contesto il piano complesso esteso è analogo alla retta reale estesa. Da un punto di vista topologico, il piano complesso esteso è effettivamente una sfera, come mostrato dalla proiezione stereografica. In analisi complessa la sfera di Riemann è la più semplice superficie di Riemann compatta e quindi un oggetto centrale della teoria, utile a definire le funzioni meromorfe.

La sfera di Riemann è centrale anche in altri campi della geometria, ad esempio in geometria proiettiva e geometria algebrica in quanto esempio fondamentale di varietà complessa, spazio proiettivo e varietà algebrica.

Costruzione

Sfera di Riemann

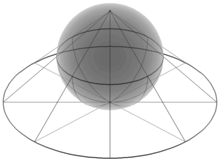
Si considera dunque una sfera tangente al piano $z=0$ nel suo polo SUD come in figura. Il polo SUD della sfera coincide con l'origine del piano complesso, rappresentato con gli assi di colore rosso. Quindi si stabilisce una corrispondenza biunivoca tra i punti della superficie sferica Z e i punti del piano complesso z (in blu nella figura). Per estensione, il punto coincidente con il polo NORD è il punto all'infinito rappresentato come $z=\infty$. Grazie a questa estensione il piano complesso diventa piano complesso chiuso e la corrispondenza biunivoca prende il nome di proiezione stereografica.

Matematicamente il punto all'infinito $z=\infty$ va trattato come un punto per il quale l'argomento è indefinito e il modulo è $+\infty$. Un intorno del punto all'infinito è l'insieme aperto $\{|z|>R\}$, cioè l'insieme dei punti maggiori di qualsiasi valore.

Funzioni sulla sfera di Riemann

Detta $S$ la sfera di Riemann, vista come il piano complesso unito con il punto $\infty$ , nel senso chiarito prima, una funzione $\phi \colon S\to S$ è detta meromorfa su $S$ se esistono due carte $\psi _{1},\psi _{2}\colon \mathbb {C} \to S$ definite come segue:

$\psi _{1}(z)=z$, ossia l'inclusione;

$\psi _{2}(z)={\frac {1}{z}},$ (ricordando la definizione precedente di ${\frac {1}{0}}=\infty$);

e tali che le composizioni con $\phi$ siano meromorfe. Si può dimostrare che le uniche funzioni meromorfe su $S$ sono le funzioni razionali (rapporti di polinomi di $\mathbb {C} [x]$), mentre discende dal teorema di Liouville che ogni funzione olomorfa sulla sfera di Riemann nel senso appena chiarito è costante.

La sfera di Riemann come varietà

La sfera di Riemann è inoltre la compattificazione di Alexandrov del piano complesso, ed è quindi omeomorfa a $\mathbb {S} ^{2},$ ma poiché vi è definita una precisa struttura complessa (ogni punto ha un intorno biolomorfo a $\mathbb {C}$) si ottiene anche che $S$ è una 1-varietà sul campo complesso. Un altro fatto che rende chiara l'importanza del ruolo rivestito dalla sfera di Riemann è una conseguenza del Teorema di uniformizzazione di Riemann, il quale afferma che le uniche 1-varietà semplicemente connesse sono il piano complesso, il piano iperbolico e la sfera di Riemann. Tra queste tre la sfera di Riemann è l'unica ad essere una superficie chiusa (ossia una superficie compatta senza bordo). Quindi $\mathbb {S} ^{2}$ ammette un'unica struttura complessa se vista come 1-varietà complessa.

Automorfismi

Nell'immagine una trasformazione di Möbius agente sul piano complesso per proiezione stereografica

Come in molte strutture matematiche, anche per la sfera di Riemann lo studio degli automorfismi presenta un interesse notevole; nel caso specifico gli automorfismi sono biolomorfismi invertibili di $S$ in sé. Le uniche funzioni che soddisfano tali requisiti sono le trasformazioni di Möbius, ossia quelle della forma

$f(\zeta )={\frac {\alpha \zeta +\beta }{\gamma \zeta +\delta }},$

con $\alpha ,\beta ,\gamma ,\delta$ numeri complessi tali che $\alpha \delta -\beta \gamma \neq 0.$

È particolarmente interessante a questo proposito ricordare la struttura che S eredita se visto come quoziente topologico di $P^{1}(\mathbb {C} )=(\mathbb {C} ^{2}\setminus \{(0,0)\})/_{\sim },$ in quanto questo consente di dare una caratterizzazione delle trasformazioni di Möbius in termini di proiettività di $\mathbb {P} ^{1}(\mathbb {C} )$. Ad esempio usando le coordinate omogenee di $\mathbb {P} ^{1}(\mathbb {C} )$ una trasformazione di Möbius può essere scritta come:

$f(a,b)=(\alpha a+\beta b,\gamma a+\delta b)={\begin{pmatrix}a&b\end{pmatrix}}{\begin{pmatrix}\alpha &\gamma \\\beta &\delta \end{pmatrix}},$

scrittura che evidenzia la corrispondenza tra le trasformazioni di questo tipo e $\mathrm {PGL} _{2}(\mathbb {C} ),$ il proiettivizzato del gruppo lineare di dimensione due sul campo complesso.

Bibliografia

• Serge Lang (1999): Complex Analysis, 4th ed., Springer, ISBN 0-387-98592-1
• Rudin, Walter, Real and Complex Analysis, New York, McGraw-Hill, 1987, ISBN 0-07-100276-6.

Voci correlate

• Analisi complessa
• Funzione olomorfa
• Superficie di Riemann
• Trasformazione di Möbius

Altri progetti

Altri progetti

• Wikimedia Commons

• Wikimedia Commons contiene immagini o altri file sulla sfera di Riemann

Collegamenti esterni

• (EN) Eric W. Weisstein, Sfera di Riemann, su MathWorld, Wolfram Research.